Leetcode 每日一题:Longest Increasing Path in a Matrix
写在前面:
今天我们继续看一道 图论和遍历 相关的题目。这道题目的背景是在一个矩阵当中找寻最长的递增数列长度。思路上非常好想,绝对和 DFS 相关,但是题目的优化要求非常高,对于语言和内存特性的考察特别丰富,如果是单纯的 Leetcoder 或者是 扎根算法而语言相对专精较弱的同学,这道题目可能很难做到 AC,就让我们一起来看看吧!
题目介绍:
题目信息:
- 题目链接:https://leetcode.com/problems/longest-increasing-path-in-a-matrix/description/
- 题目类型:Array,Graph,DFS,Dynamic Programming(是的,可以拿 dp 做,但是太难了而且并不具备推广价值,所以不分享了)
- 题目难度:Hard(思路 easy,优化要求 hard)
- 题目来源:Google 高频面试真题
题目问题:
- 给定一个大小为 m * n 的矩阵,每一个矩阵的位置都代表一个 value
- 找出最长的 递增遍历行走路线
- 在行走的过程中,只能上下左右,不能走对角线
- 例子:

题目想法:
深度优先暴力解法:
一看到是走 “最长的递增” 数组,并且在图中只能上下左右移动,我们很容易可以想到 DFS,这也是一个标准的 DFS 问题。我们只需要遍历每一个位置当作起点,并且不断寻找周围有没有递增的位置可以让我们前进,返回当前起点所能达到的最大值。将所有的最大值统筹起来,进行返回。
很可惜,思路很美好,现实很骨感,这样的做法不仅会 TLE,而且会 MLE,在算法时间复杂度和占用空间内存的角度来讲都会爆炸。
Runtime:O(2^(m+n)) --> 我们需要遍历所有可能的子数组
Space:O(mn) --> 我们最坏需要遍历所有的 node 和 edge,并且,需要mn次 stack 来储存
太慢,也太耗空间了(如果懂得堆栈的小伙伴应该知道太多 recursion 会占掉很多内存)
时间复杂度优化:
暴力解法非常简单想到,那 Google 和 其他大厂的要求肯定不止这么一点儿~~ 但如果自己想想,我们每一次以一个点为起点进行探索的时候,我们的目标都是取得这个点所能创造的最大长度,从而决定我们是否有机会获得更好的结果。那我们是否可以利用 Memoization 的方法,将每个遍历过后的点的最大值记下来,这样之后的重复使用不就都不用再遍历了吗?
我们在从每一个点开始遍历 DFS 的时候,将所有路过的点的最大值进行一个更新,而我们在找寻起点的过程中,就可以直接从这些点里取值了,因为他一定是最大的。
为什么一定如果一个点被遍历过之后存下的结果一定 >= 我们以这个点为起点重新遍历呢?
- 如果这个点的现有最大值是从本点开始,那再来一次遍历也会得到相同结果
- 如果这个点的现有最大值是从一个比他更小的点得来的,那以他自己为起点此次结果一定会小于我们所存储的节点,因为单调递增的单向性
- 而这个点的现有最大值不可能来自己于一个比他更大的起点
- 所以总结,存下的结果 >= 以当前为起点遍历可能最大 ---> 当前存储的结果一定是最优的
Runtime:O(mn) ---> 我们只需要遍历一次图即可,可以被 AC
Space:O(mn) ---> 我们需要存储所有的矩阵点的最大值
内存优化:
虽然这道题的 O(mn) 的空间复杂度已经是最优复杂度了,但不同的 implementation 同样会导致 AC 和 MLE 的区别,题主自己在做这道题的时候,经过了算法的优化以后还是 MLE,后来经过对数据结构和 recursion 变量的优化才最终解决内存问题,这可能也是大厂对代码水平更高难度的考察吧,这也是我认为这道题是 hard 的一部分原因
如果使用 C++ 进行代码编写,可以优化的点有:
- 对于数据的存储,不使用 vector, 而是使用 dynamic array 进行内存分配
- 对于Recursion函数传入的矩阵和记忆矩阵,把他们变成 member variable,在recursion中静态调用,而不是不停的动态参数传入
第一个问题的原因是基于 vector 的特性。在 C++中,动态数组的内存分布并不是按照有多少个元素来分配的,而是分配 2^n 个储存空间,n 是让 2^n 大于所需长度的最小值。而这样的分配方式会造成内存浪费。例如:一个长度为 7 的 vector 实际上占用了 8 个长度的内存,而长度为 9 的 vector 实际上占用了 16 个长度的内存。而如果使用 dynamic allocation,在 matrix 长度宽度已知不会变的情况下,我们完全可以手动分配内存,精准的将 矩阵的维度 分配出来。在 2 个维度同时减少内存浪费,省去非常多的空间
第二个问题的原因是,没有一次 recursion function call,这个函数就会在内存中开辟一段储存空间,而如果我们将 矩阵和记忆矩阵作为变量不断传入,他们就会不断的在内存 stack 中生成很多很多 copy,从而导致 stack 崩掉。而如果我们将其改成 member variable,他们相对于所有的 recursion 函数就是全局的,每个 recursion 都只需要直接调用他的指针所指的真实数据,而不是 copy,这也会节省更多空间
在同时完成这两个优化以后,相信大家也能成功 AC 这道 Leetcode hard
题目代码:
class Solution {
public:int x[4] = {0, 1, 0, -1};int y[4] = {1, 0, -1, 0};int** maxViewed; //use dynamic array instead of vector to prevent memory wasteint** matrix; //use member variable instead of arguement in recursion to prevent //too much stack memory wasted in recursionint DFS(int i, int j, int m, int n){//we have already seen this point, so need to traverse. if(maxViewed[i][j] != 0){return maxViewed[i][j];}for(int d = 0; d < 4; d++){int new_i = i + x[d];int new_j = j + y[d];//check in bound, no need to check revisit, but have check for increasingif(new_i < m && new_i >= 0 && new_j < n && new_j >= 0){if(matrix[i][j] < matrix[new_i][new_j]){maxViewed[i][j] = max(DFS(new_i, new_j, m, n), maxViewed[i][j]);}}}maxViewed[i][j] += 1;return maxViewed[i][j];}int longestIncreasingPath(vector<vector<int>>& matrix_target) {int maxDist = 0;int m = matrix_target.size(), n = matrix_target[0].size();//create a cache and matrix storage for the traversing:maxViewed = new int*[m]; // Allocate memory for rowsmatrix = new int*[m];for (int i = 0; i < m; ++i) {maxViewed[i] = new int[n]; // Allocate memory for columnsmatrix[i] = new int[n];}for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){maxViewed[i][j] = 0;matrix[i][j] = matrix_target[i][j];}}for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){maxDist = max(maxDist, DFS(i, j, m, n));}}return maxDist;}
};相关文章:

Leetcode 每日一题:Longest Increasing Path in a Matrix
写在前面: 今天我们继续看一道 图论和遍历 相关的题目。这道题目的背景是在一个矩阵当中找寻最长的递增数列长度。思路上非常好想,绝对和 DFS 相关,但是题目的优化要求非常高,对于语言和内存特性的考察特别丰富,如果是…...

ARCGIS PRO DSK MapTool
MapTool用于自定义地图操作工具,使用户能够在ArcGIS Pro中执行特定的地图交互操作。添加 打开MapTool1.vb文件,可以看到系统已经放出MapTool1类: Public Sub New()将 IsSketchTool 设置为 true 以使此属性生效IsSketchTool TrueSketchTyp…...

国网B接口 USC安防平台 海康摄像机配置
国网B接口海康摄像机配置介绍 如下以海康DS-NACN6432I-GLN摄像机为例,配置国网B接口设备接入流程,海康摄像机的固件版本为 V5.6.11 build 210109 210107。该设备为球机,支持国网B接口云台控制功能。图标编号可以对应二者的配置。 注意 同一…...

Win10安装.net FrameWork3.5失败解决方法
win10安装.net FrameWork3.5失败解决方法 已经好久没有来投稿了,实在最近业务缠身,忙的焦头烂额(呵~多么伟大的牛马) 但最近开发使用windows11实在是拉胯的不行,升级完就后悔,所以就一怒之下,重装了win10 可是,好家伙,我重装完遇到一个问题,就是在使用.Net Framework3.5,按照Mi…...

【pipenv】—— 虚拟环境管理工具近乎全面的总结
安装 pip install pipenv 使用和配置 设置虚拟环境文件创建在项目根目录 添加环境变量:WORKON_HOMEPIPENV_VENV_IN_PROJECT 创建虚拟环境时,自动换用指定的pip源 添加环境变量:PIPENV_TEST_INDEXhttps://pypi.tuna.tsinghua.edu…...
 -选择排序算法)
windows C++-并行编程-并行算法(五) -选择排序算法
并行模式库 (PPL) 提供了对数据集合并行地执行工作的算法。这些算法类似于 C 标准库提供的算法。并行算法由并发运行时中的现有功能组成。 在许多情况下,parallel_sort 会提供速度和内存性能的最佳平衡。 但是,当您增加数据集的大小、可用处理器的数量或…...

【系统架构设计师-2014年真题】案例分析-答案及详解
更多内容请见: 备考系统架构设计师-核心总结索引 文章目录 【材料1】问题1问题2【材料2】问题1问题2问题3【材料3】问题1问题2问题3【材料4】问题1问题2【材料5】问题1问题2问题3【材料1】 请详细阅读以下关于网络设备管理系统架构设计的说明,在答题纸上回答问题1和问题2。 …...
-分区工作)
windows C++-并行编程-并行算法(三)-分区工作
并行模式库 (PPL) 提供了对数据集合并行地执行工作的算法。这些算法类似于 C 标准库提供的算法。并行算法由并发运行时中的现有功能组成。 若要对数据源操作进行并行化,一个必要步骤是将源分区为可由多个线程同时访问的多个部分。 分区程序将指定并行算法应如何在线…...

下载 llama2-7b-hf 全流程【小白踩坑记录】
1、文件转换 在官网 https://ai.meta.com/llama/ 申请一个账号,选择要下载的模型,会收到一个邮件,邮件中介绍了下载方法 执行命令 git clone https://github.com/meta-llama/llama.git ,然后执行 llama/download.sh,…...

Codeforces practice C++ 2024/9/11 - 2024/9/13
D. Mathematical Problem Codeforces Round 954 (Div. 3) 原题链接:https://codeforces.com/contest/1986/problem/D 题目标签分类:brute force,dp,greedy,implementation,math,two pointers…...

RabbitMQ创建交换机和队列——配置类 注解
交换机的类型 Fanout:广播,将消息交给所有绑定到交换机的队列。 Direct:订阅,基于RoutingKey(路由key)发送给订阅了消息的队列。 Topic:通配符订阅,与Direct类似,只不…...

proteus+51单片机+AD/DA学习5
目录 1.DA转换原理 1.1基本概念 1.1.1DA的简介 1.1.2DA0832芯片 1.1.3PCF8591芯片 1.2代码 1.2.1DAC8053的代码 1.2.2PCF8951的代码 1.3仿真 1.3.1DAC0832的仿真 1.3.2PFC8951的仿真 2.AD转换原理 2.1AD的基本概念 2.1.1AD的简介 2.1.2ADC0809的介绍 2.1.3XPT2…...

【Python机器学习】长短期记忆网络(LSTM)
目录 随时间反向传播 实践 模型的使用 脏数据 “未知”词条的处理 字符级建模(英文) 生成聊天文章 进一步生成文本 文本生成的问题:内容不受控 其他记忆机制 更深的网络 尽管在序列数据中,循环神经网络为对各种语言关系…...

【Go】使用Goland创建第一个Go项目
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

STM32学习笔记(一、使用DAP仿真器下载程序)
我们想要使用32单片机,总共包含四个步骤: 1、硬件连接 2、仿真器配置 3、编写程序 4、下载程序 一、第一个问题(硬件连接):如何进行硬件连接,才能够启动32板子并能够下载程序呢? 答&#…...
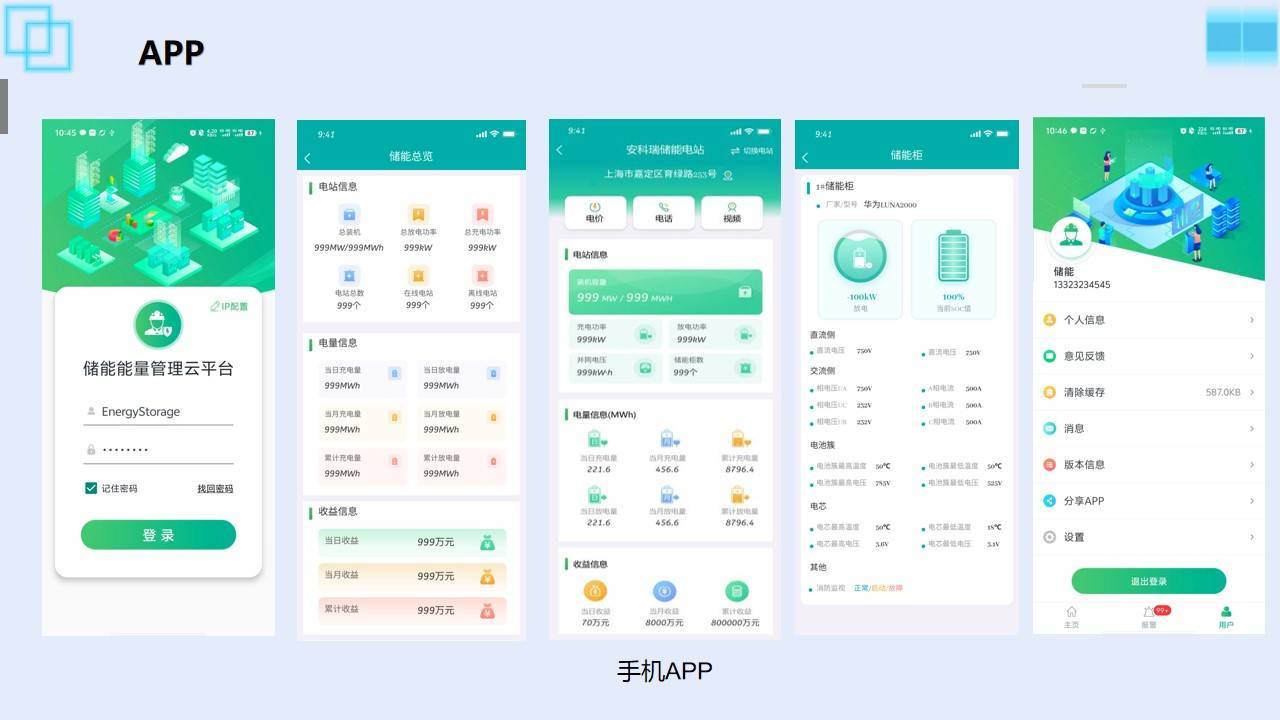
储能运维管理云平台解决方案EMS能量管理系统
在储能行业蓬勃发展的今天,储能运维管理的重要性日益凸显。而储能运维管理云平台的出现,正为储能系统的稳定运行和高效管理注入了新的活力。 一、储能运维管理面临的挑战 传统的储能运维管理方式往往依赖人工巡检和现场操作,存在诸多问题。比…...

网络药理学:16、速通流程版
一、筛选疾病靶点 GeneCards 下载数据得到GeneCards-SearchResult.csv通过Relevance score≥1.0得到GeneCards.csv步骤2只保留Gene Symbol,即基因名这一列得到GeneCards_gene_names.csv OMIM 下载数据得到OMIM-Gene-Map-Retrieval.xlsx只保留Gene/Locus…...

P2515 [HAOI2010] 软件安装
~~~~~ P2515 [HAOI2010] 软件安装 ~~~~~ 总题单链接 思路 ~~~~~ 发现构成的图是一个森林和一些环。 ~~~~~ 对于森林,建一个虚点然后树形 D P DP DP 即可。 ~~~~~ 对于环,发现要么把这个环上的每一个点都选了,要么每一个都不选。所以可以先缩…...

51单片机快速入门之定时器和计数器
51单片机快速入门之定时器 断开外部输入 晶振振荡 假设为 12MHz 12分频之后,为1MHz 当其从0-65536 时,需要65536μs 微秒 也就是65.536ms 毫秒 溢出(值>65536 时)>中断>执行中断操作 假设需要1ms后产生溢出,则需要设置初始值为64536 此时定时器会从 64536 开始计…...

【计算机网络 - 基础问题】每日 3 题(一)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/fYaBd 📚专栏简介:在这个专栏中,我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏&…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

