动态规划-不同的子序列
题目描述
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
示例:
输入:s = "babgbag", t = "bag"
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
为了解决这个问题,我们首先需要理解题目中的关键概念:“子序列”和“出现的个数”。子序列是指从原字符串中删除一些(或者不删除)字符而不改变剩余字符的相对顺序所得到的新字符串。例如,字符串 "abc" 的子序列包括 "a", "b", "c", "ab", "ac", "bc", "abc", ""(空字符串)等。
接下来,我们要计算在字符串 s 的所有子序列中,字符串 t 出现的次数。这可以通过动态规划(Dynamic Programming, DP)来有效地解决。
解题思路
我们可以使用二维数组 dp[i][j] 来表示状态,其中 dp[i][j] 表示 s 的前 i 个字符(即 s[0...i-1])中包含 t 的前 j 个字符(即 t[0...j-1])作为子序列的个数。注意这里的 i 和 j 都是从 1 开始的,方便处理边界情况。
-
初始化:
dp[0][j] = 0对于所有的j(因为空字符串不包含任何非空字符串的子序列),dp[i][0] = 1对于所有的i(因为任何字符串都包含空字符串作为子序列)。 -
状态转移方程:
- 如果
s[i-1] == t[j-1],则有两种情况:- 包含当前字符
s[i-1]作为t[j-1]的一部分:dp[i-1][j-1] - 不包含当前字符
s[i-1]:dp[i-1][j]
因此,dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。
- 包含当前字符
- 如果
s[i-1] != t[j-1],则只有一种情况:- 不包含当前字符
s[i-1]:dp[i-1][j]
因此,dp[i][j] = dp[i-1][j]。
- 不包含当前字符
- 如果
-
结果:
dp[n][m],其中 n 和 m 分别是字符串s和t的长度。
怎样想到这样状态方程的?
一点个人经验,见过的很多2个串的题,大部分都是dp[i][j] 分别表示s串[0...i] 和t串[0...j]怎么怎么样然后都是观察s[i]和t[j]分等或者不等的情况 而且方程通常就是 dp[i-1][j-1] 要么+ 要么 || dp[i-1][j]类似的。
class Solution {
public:const int MOD = 1e9 + 7;int numDistinct(string s, string t) {int n = s.size();int m = t.size();vector<vector<int>> dp(n+1, vector<int>(m+1, 0));//dp[i][j]: t[0~j]子串在 s[0~i]子序列中出现的个数for(int i=0;i<n;i++){ dp[i][0] = 1;//空字符串是任何字符串的子序列}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j>i)continue;//无法在较小的字符串中出现更大的字符串if(s[i-1] == t[j-1]){dp[i][j] = (dp[i-1][j-1] + dp[i-1][j])%MOD;}else{dp[i][j] = dp[i-1][j];}}} return dp[n][m]; }
};相关文章:

动态规划-不同的子序列
题目描述 给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 7 取模。 示例: 输入:s "babgbag", t "bag" 输出:5 解释: 如下所示, 有 5 种可以从…...
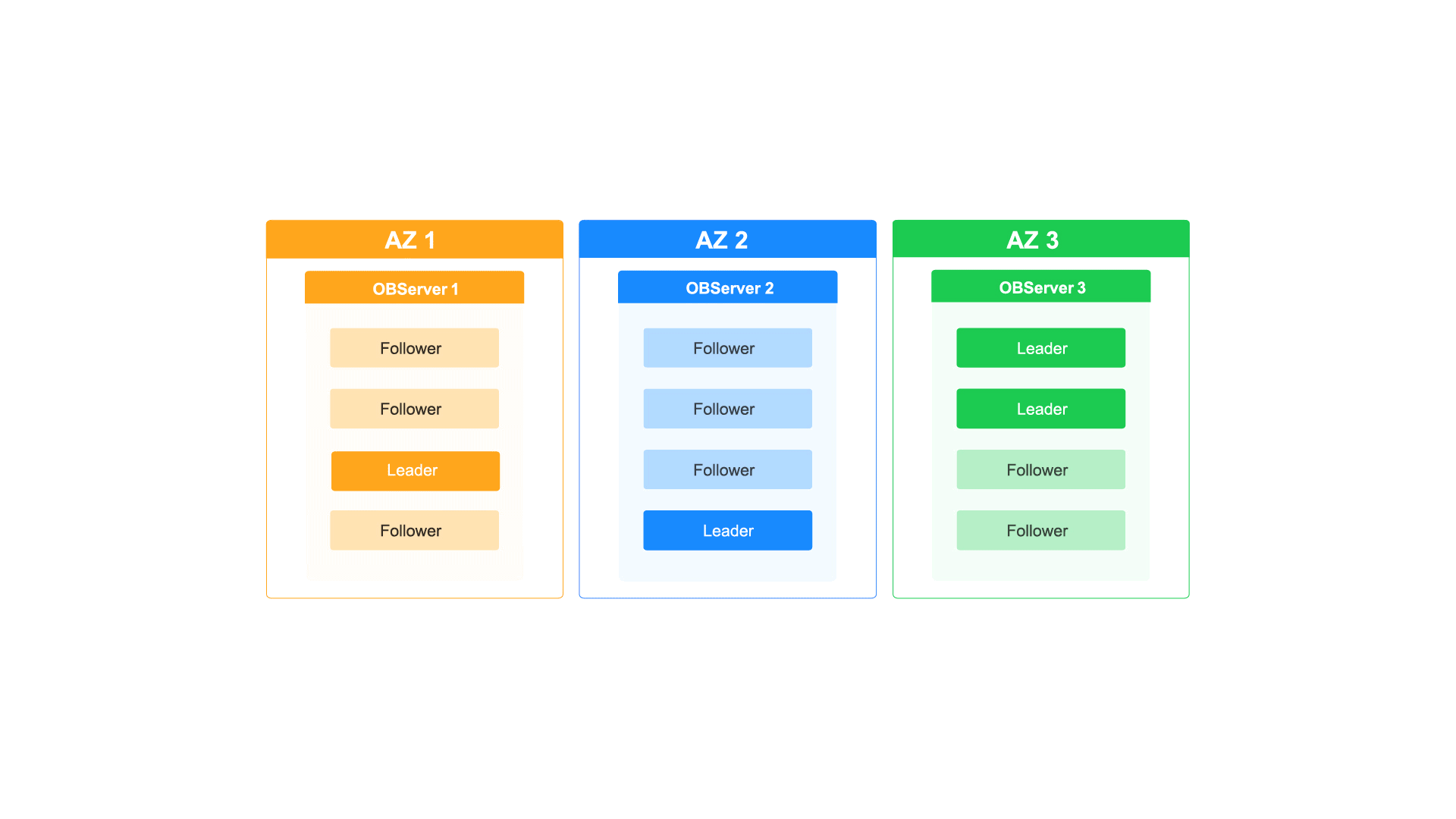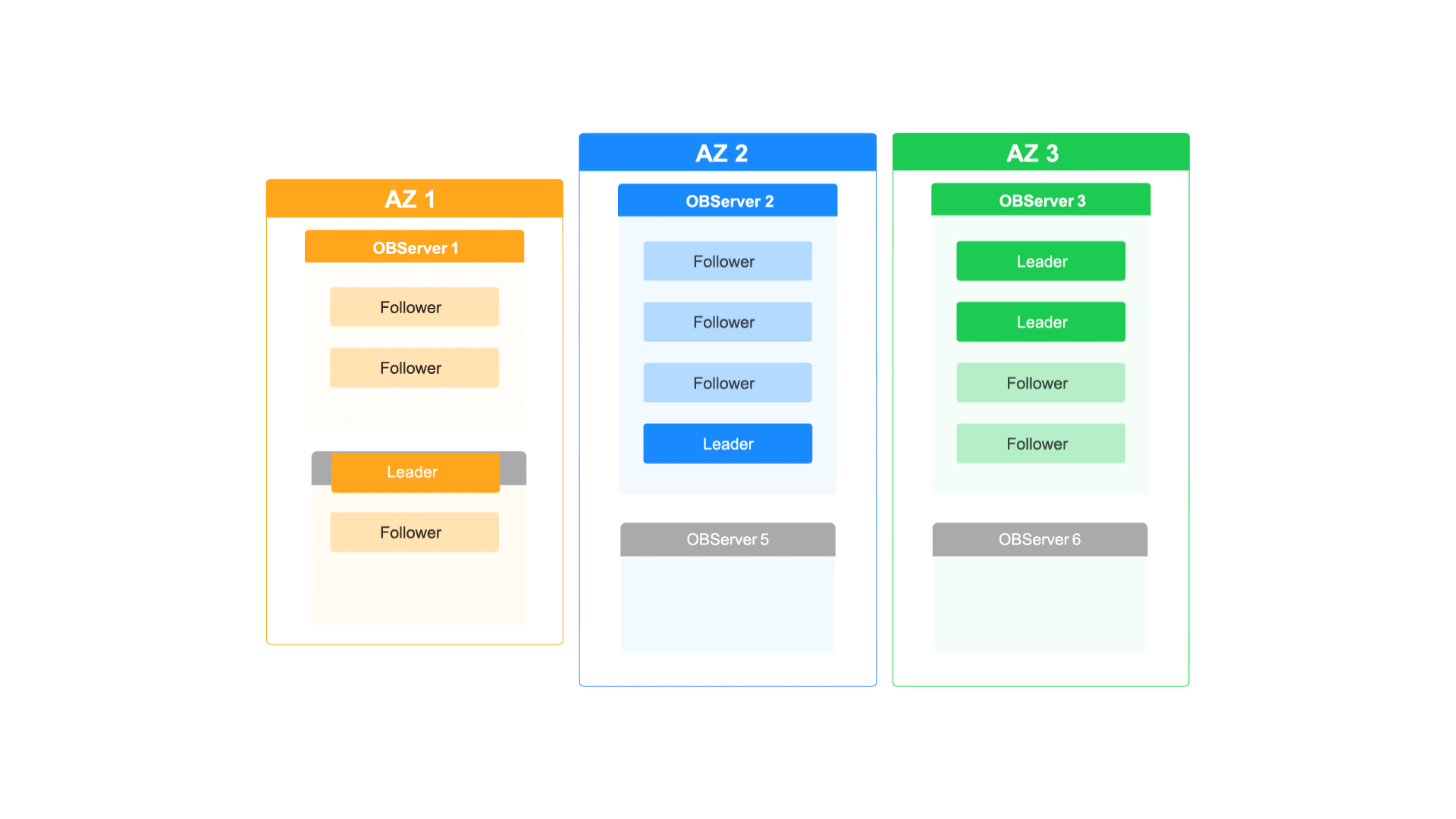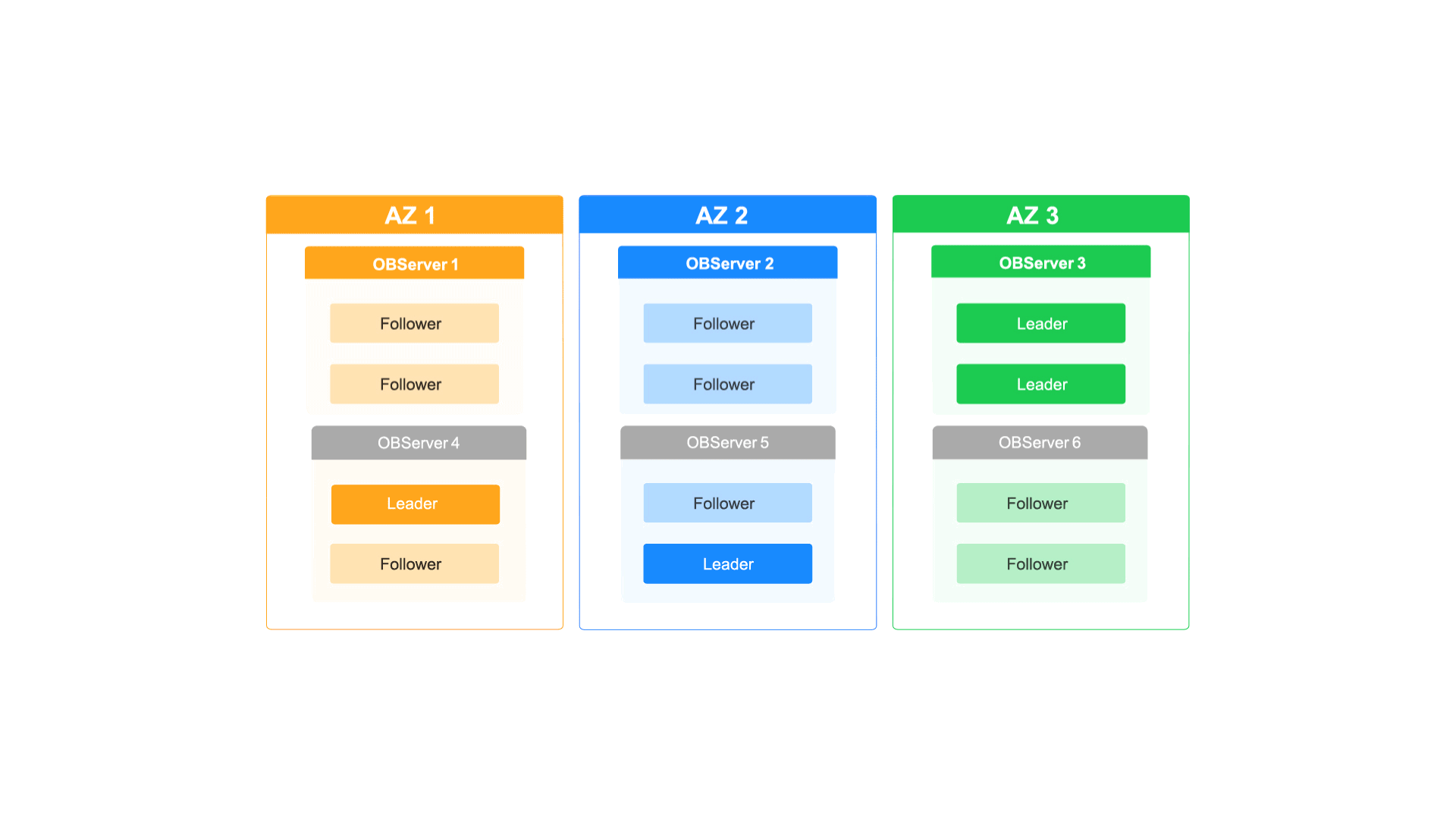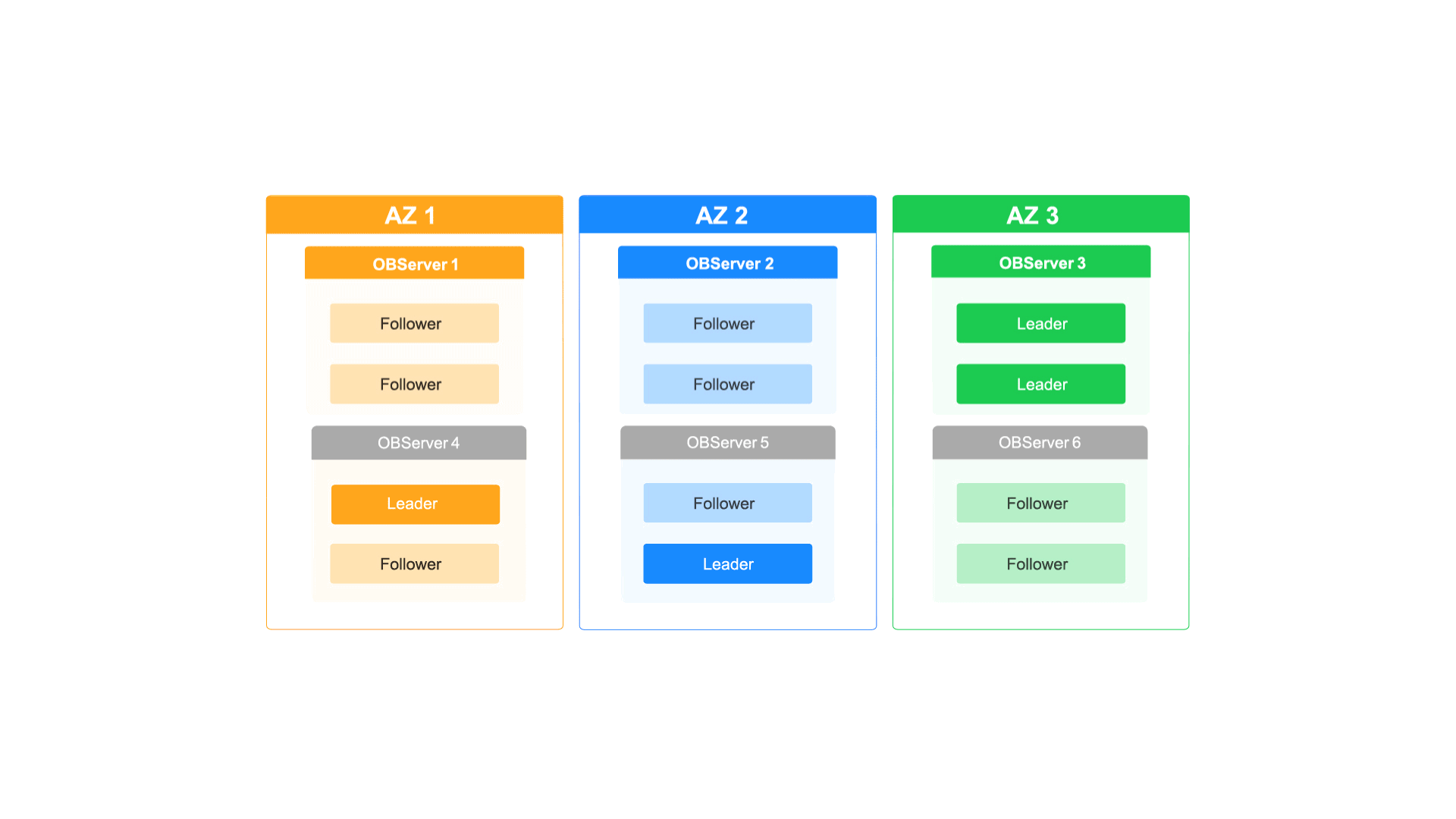
如何通过OceanBase的多级弹性扩缩容能力应对业务洪峰
每周四晚上的10点,都有近百万的年轻用户进入泡泡玛特的抽盒机小程序,共同参与到抢抽盲盒新品的活动中。瞬间的并发流量激增对抽盒机小程序的系统构成了巨大的挑战,同时也对其数据库的扩容能力也提出了更高的要求。 但泡泡玛特的工程师们一点…...

D - 1D Country(AtCoder Beginner Contest 371)
题目链接: D - 1D Country (atcoder.jp) 题目描述: 数据范围: 输入输出: 题目分析: 典型的l, r 区间问题,即是前缀和问题,但是注意到数据范围, 数据范围1e-9 到 1e9 数据范围,要是从最小到最大直接for循环去模拟的话,时间复杂度…...
怎么很多张图片拼接成一张?试试这几种图片拼接方法!
怎么很多张图片拼接成一张?在繁忙的现代生活中,我们不断地捕捉和累积着各式各样的图像,它们如同记忆的珍珠,串联起生活的每一个瞬间,然而,随图片数量的激增,管理它们成为了一项挑战,…...

Python实现优化的分水岭算法
目录 优化分水岭算法的博客1. 分水岭算法优化概述2. 优化分水岭算法的步骤3. Python实现优化后的分水岭算法4. 实例:优化分水岭算法在图像分割中的应用5. 总结 优化分水岭算法的博客 分水岭算法是一种强大的图像分割方法,特别适用于分离不同的对象和区域…...

智慧交通基于yolov8的行人车辆检测计数系统python源码+onnx模型+精美GUI界面
【算法介绍】 智慧交通中,基于YOLOv8的行人车辆检测计数系统是一项高效、准确的技术解决方案。该系统利用YOLOv8这一先进的目标检测算法,结合深度学习技术,能够实时检测并准确计数道路上的行人和车辆。YOLOv8在保证检测速度的同时࿰…...

Linux开发工具的使用
文章目录 vim的使用基本模式介绍光标当前行操作(命令行模式)光标快速定位(命令行模式):插入模式的三种方式(命令行模式):vim基本操作(命令行模式)底行模式的操…...
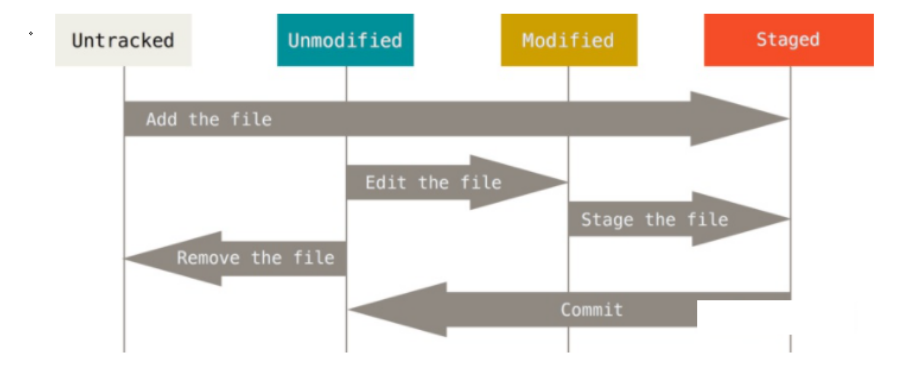
【devops】devops-git之介绍以及日常使用
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

012复杂度07leetcode
视频地址:012复杂度07leetcode_哔哩哔哩_bilibili 网站叫做leetcode。那Linux我相信很多同学都听过这个网站,那这个网站干嘛用呢?这个网站是用于练习算法的一个好网站,那我们这个课程在讲解知识点过程中也会不断的去用到这个网站,…...

4.网络编程
1、目的 传播交流信息TCP:打电话UDP:发短信 2、通信协议: httpTCP/IP簇:三次握手(aba),四次挥手(abba)https 3、IP与端口 1.IP地址类:InetAddress、InetSocketAddress InetAdd…...
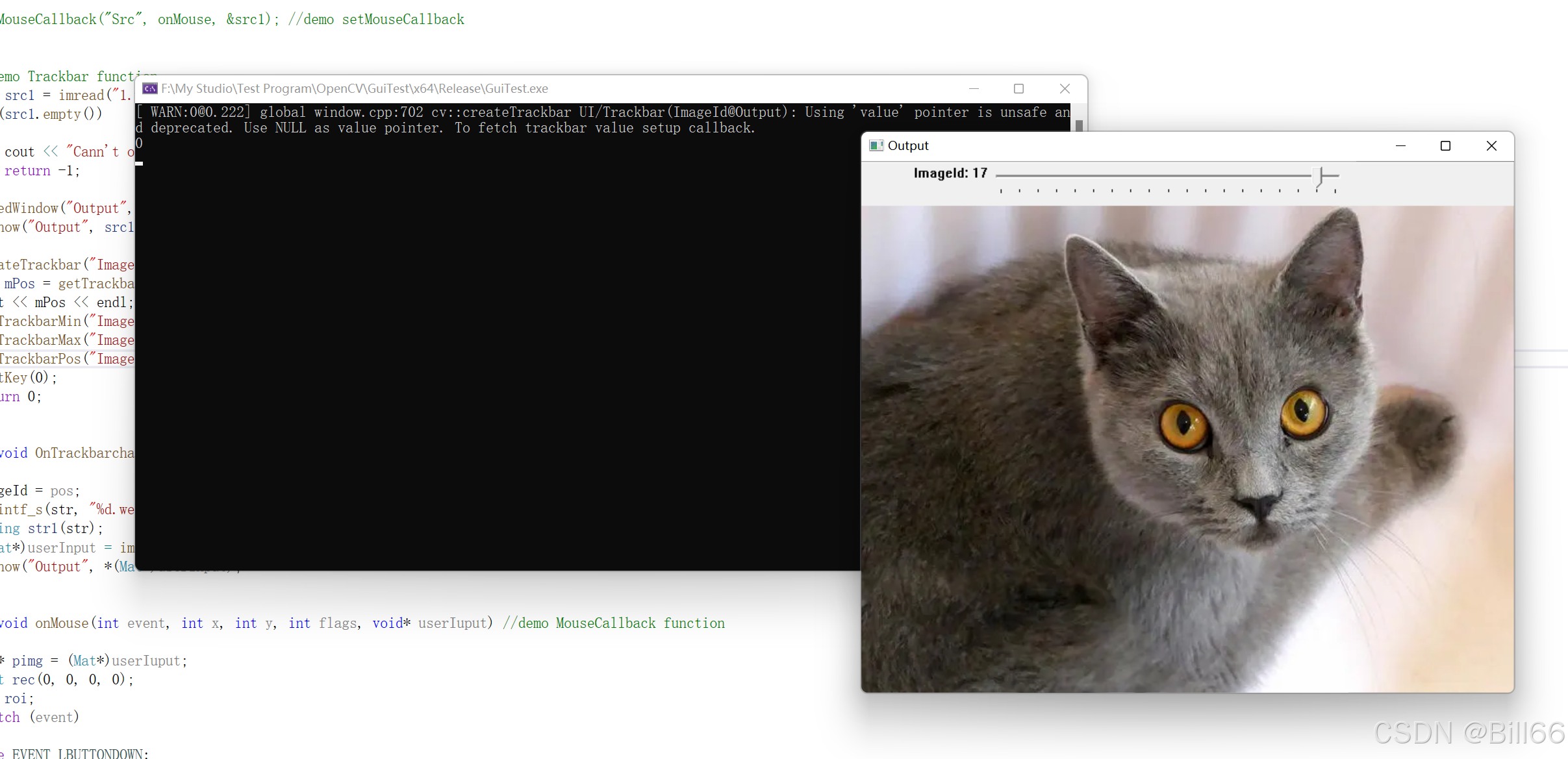
OpenCV GUI常用函数详解
在OpenCV的High_level GUI模组中有很多GUI函数,下面介绍几个常用的函数。 图像显示窗口相关函数 生成图像显示窗口函数nameWindow() nameWindow()函数的原型如下: 函数用以创建一个给定名的图像显示窗口(后面简单叫做图像窗口)…...
Tuxera NTFS for Mac破解版下载 Tuxera NTFS for Mac2023激活码 mac电脑ntfs磁盘软件
Tuxera NTFS for Mac是一款优秀的Mac系统完全读写软件,提供Fat32、NTFS、Exfat、mac os扩展格式的转换,稳定性好,传输速度极快。Tuxera NTFS for Mac功能丰富,能修复NTFS卷、创建NTFS磁盘映像、创建NTFS分区等等。同时软件支持所有…...
基于备份集搭建备租户方式)
oceanbase(ob)基于备份集搭建备租户方式
一、搭建备租户方式(基于备份的方式) 注意事项:要有一个源端OB集群和目标端OB集群。 1、新建主租户(如果原来有主租户可是省略) #创建unit create resource unit ut_2c2g max_cpu2, memory_size2G, max_iops10000,l…...

Javase复习day21算法、arrays、Lamdba表达式
常见算法 查找算法 基本查找 package search;public class BasicSearchDemo1 {public static void main(String[] args) {//基本算法(顺序查找)int[] arr {131,23,57,37,95,48,57,43};System.out.println(basicSearch(arr, 43));}public static boo…...

移动硬盘无法读取?别慌!这些方法助你恢复数据!
在我们的日常工作和生活中,移动硬盘作为重要的数据存储工具,承载着珍贵资料。然而,移动硬盘无法被电脑读取的情况时有发生,令人焦急。别慌,下面为大家详细介绍恢复移动硬盘数据的有效方法。 一、检查硬件连接和驱动问题…...
)
Java集合面试(上)
Java集合面试(上) 集合概述 Java 集合,也叫作容器,主要是由两大接口派生而来:一个是 Collection接口,主要用于存放单一元素;另一个是 Map 接口,主要用于存放键值对 说说List,Set,Queue&#…...

Python画笔案例-046 绘制小红伞
1、绘制小红伞 通过 python 的turtle 库绘制 小红伞,如下图: 2、实现代码 绘制 小红伞,以下为实现代码: """小红伞.py """ import turtledef draw_pattern():"""画填充圆弧"&…...

使用 .NET 6 构建跨平台 Worker Service 服务:跨越平台的 C# 服务开发——解决Windows服务跨平台问题
现代软件开发中,构建跨平台的应用程序变得愈加重要。C# 和 .NET 6 的出现使得在 Windows、Linux 和 macOS 上创建背景服务变得简单而高效。在本指南中,我们将通过创建一个使用 .NET 6 的 Worker Service 来展示如何实现跨平台后台服务。 项目概述 我们…...

terminator-gnome
gnome import os#启动节点指令变量 stere"ros2 launch stereo_c start.py" utils"ros2 launch task utils.launch.py" #tab标题 stere_title"stere_driver" utils_title"utils"#一个终端界面打开5个tab cmd1f"gnome-terminal --…...
7.测试用例设计方法 + Bug
一、正交实验法 1.使用场景 因果关系比较庞大的情况下,不太适合用因果图判定表,在这种情况下,一般会采用正交实验法。 2.例子: 字符属性设置(4个条件) 字体很多 字符样式很多 …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
