最大流笔记
概念
求两点间的路径中可在同一时间内通过的最大量
EK算法
通过bfs找通路,找到后回溯;
每确定一条边时,同时建立一天反方向的边以用来进行反悔操作(毕竟一次性找到正确方案的概率太低了)
code
#include<bits/stdc++.h>
#define ll long long
#define inl inline
#define re register
using namespace std;
inl int read() {int sum=0,f=1;char c=getchar();while(!isdigit(c)) {if(c=='-') f=-1;c=getchar();}while(isdigit(c)) {sum=(sum<<3)+(sum<<1)+(c^48);c=getchar();}return sum*f;
}
const int N=210;
int dis[10000010],ans,head[N<<1],tot=1,n,m,f[210][210];
struct node{int to,w,nxt;
}e[10000010];
inl void add(int u,int v,int w) {e[++tot].to=v;e[tot].w=w;e[tot].nxt=head[u];head[u]=tot;e[++tot].to=u;e[tot].w=0;e[tot].nxt=head[v];head[v]=tot;
}
bool vis[210];
int pre[N];
inl bool bfs() {memset(vis,0,sizeof(vis));queue<int> q;dis[1]=100000000;vis[1]=1;q.push(1);while(!q.empty()) {int u=q.front();q.pop();for(re int i=head[u];i;i=e[i].nxt) {int v=e[i].to;if(vis[v]==1 || e[i].w==0) continue;dis[v]=min(dis[u],e[i].w) ;//cout<<dis[v]<<endl;pre[v]=i;q.push(v);vis[v]=1;if(v==n) return 1;}}return 0;
}
inl void update() {int u=n;while(u!=1) {int v=pre[u] ;e[v].w-=dis[n];e[v^1].w+=dis[n];u=e[v^1].to;}ans+=dis[n];
}
int main() {m=read(),n=read();for(re int i=1;i<=m;i++) {int u=read(),v=read(),w=read();if(!f[u][v]) {add(u,v,w);f[u][v]=tot;}else{e[f[u][v]-1].w+=w;}}while(bfs()) {//cout<<dis[n]<<endl;update();}cout<<ans<<endl;return 0;
}Dinic算法
也是运用bfs将原图进行分层,但统计答案时使用dfs,,可大大降低时间复杂度
code
#include<bits/stdc++.h>
#define ll long long
#define re register
#define inl inline
using namespace std;
inl int read() {int sum=0,f=1;char c=getchar();while(!isdigit(c)) {if(c=='-') f=-1;c=getchar();}while(isdigit(c)) {sum=(sum<<3)+(sum<<1)+(c^48);c=getchar();}return sum*f;
}
const int N=210;
int n,m,x,head[N<<1],f[210][210],tot=1,cur[N*N],ans,d[N];
struct node{int to,nxt,w;
}e[N*N+1000];
inl void add(int u,int v,int w) {//cout<<1<<endl;e[++tot].to=v;e[tot].w=w;e[tot].nxt=head[u];head[u]=tot;e[++tot].to=u;e[tot].w=0;e[tot].nxt=head[v];head[v]=tot;
}
inl bool bfs() {memset(d,0,sizeof(d));queue<int> q;d[1]=1;q.push(1);while(!q.empty()) {int u=q.front() ;q.pop();for(re int i=head[u];i;i=e[i].nxt) {int v=e[i].to;if(!d[v] && e[i].w) {d[v]=d[u]+1;q.push(v);if(v==n) return 1;}}}return 0;
}
inl int dfs(int u,int mf) {if(u==n) return mf;int tmp=0;for(int i=cur[u];i;i=e[i].nxt) {cur[u]=i;int v=e[i].to;if(d[v]==d[u]+1 && e[i].w) {int tmp1=dfs(v,min(mf,e[i].w));e[i].w-=tmp1;e[i^1].w+=tmp1;tmp+=tmp1;mf-=tmp1;if(!mf) break;}}if(!tmp) d[u]=0;return tmp;
}
inl void dinic() {while(bfs()) {memcpy(cur,head,sizeof head);ans+=dfs(1,100000000);}
}
int main() {n=read();m=read();x=read();//cout<<n<<" "<<m<<" "<<x<<endl;for(re int i=1;i<=m;i++) {int u=read(),v=read(),w=read();if(!f[u][v]) {add(u,v,w);f[u][v]=tot;}else{e[f[u][v]-1].w+=w;}}dinic();if(!ans) {puts("Orz Ni Jinan Saint Cow!");}else {int p=x/ans;if(p*ans<x) {p++;}printf("%d %d\n",ans,p);}return 0;
}相关文章:

最大流笔记
概念 求两点间的路径中可在同一时间内通过的最大量 EK算法 通过bfs找通路,找到后回溯; 每确定一条边时,同时建立一天反方向的边以用来进行反悔操作(毕竟一次性找到正确方案的概率太低了) code #include<bits/st…...

el-tree父子不互相关联时,手动实现全选、反选、子级全选、清空功能
el-tree父子不互相关联时,手动实现全选、反选、子级全选、清空功能 1、功能实现图示 2、实现思路 当属性check-strictly为true时,父子节点不互相关联,如果需要全部选中或选择某一节点下的全部节点就必须手动选择每个节点,十分麻…...
入门篇)
模板与泛型编程笔记(一)入门篇
1. 推荐书籍 《C新经典 模板与泛型编程》难得的很容易看得懂的好书,作者讲技术不跳跃,娓娓道来,只要花点时间就能看懂。 2. 笔记 2.1 模板基础 模板为什么要用尖括号?因为便于编译器解析,可以将模板和普通函数声明…...

浅谈WebApi
一、基本介绍 Web API(Web应用程序编程接口)是一种用于构建应用程序的接口,它允许软件应用程序通过HTTP请求与Web服务器进行交互。Web API通常用于构建客户端-服务器应用程序,其中客户端可以是Web浏览器、移动应用程序、桌面应用程…...

9月14日,每日信息差
第一、宝马集团宣布对设计部门进行重组,并将于 2024 年 10 月 1 日成立一个跨品牌设计团队,由范・霍伊顿克领导。该团队将引入极星汽车设计主管马克西米利安・米索尼,负责宝马中高档和豪华车型以及宝马 Alpina 的设计工作。 第二、小鹏汇天飞…...

无人机控制与三维AI感知处理平台正式上线!
低空经济被誉为推动我国经济高质量发展的全新增长引擎,是一种以民用有人驾驶和无人驾驶航空器的各类低空飞行活动为牵引,辐射带动相关领域融合发展的综合性经济形态,2024年全国两会首次被纳入政府工作报告。 大势智慧积极响应国家低空经济政…...

9.11-kubeadm方式安装k8s
一、安装环境 编号主机名称ip地址1k8s-master192.168.2.662k8s-node01192.168.2.773k8s-node02192.168.2.88 二、前期准备 1.设置免密登录 [rootk8s-master ~]# ssh-keygen [rootk8s-master ~]# ssh-copy-id root192.168.2.77 [rootk8s-master ~]# ssh-copy-id root192.168…...

限流,流量整形算法
写在前面 源码 。 本文看下流量整形相关算法。 目前流量整形算法主要有三种,计数器,漏桶,令牌桶。分别看下咯! 1:计数器 1.1:描述 单位时间内只允许指定数量的请求,如果是时间区间内超过指…...

【C++知识扫盲】------C++ 中的引用入门
在 C 中,引用(reference) 是一个非常重要的概念,它提供了一种别名机制,让我们可以给已经存在的变量起一个新的名字,并且能够通过这个别名直接操作原始变量。本文将详细介绍引用的定义、使用场景及其与指针的…...

【机器学习】6 ——最大熵模型
机器学习6——最大熵模型 目录 机器学习6——最大熵模型最大熵(maximum entropy)模型模型模型学习(估计参数)模型评价应用 最大熵(maximum entropy)模型 选择熵最大的概率模型 熵是衡量不确定性的…...

小程序——生命周期
文章目录 运行机制更新机制生命周期介绍应用级别生命周期页面级别生命周期组件生命周期生命周期两个细节补充说明总结 运行机制 用一张图简要概述一下小程序的运行机制 冷启动与热启动: 小程序启动可以分为两种情况,一种是冷启动,一种是热…...

基于微信小程序的宠物之家的设计与实现
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 基于微信小程序JavaSpringBootVueMySQL的宠物之家/宠物综合…...

自定义EPICS在LabVIEW中的测试
继续上一篇:LabVIEW中EPICS客户端/服务端的测试 变量定义 You can use CaLabSoftIOC.vi to create new EPICS variables and start them. CA Lab - LabVIEW (Realtime) EPICS INPUT: PV set Cluster-array of names, data types and field definitions to crea…...

基于深度学习的农作物病害检测
基于深度学习的农作物病害检测利用卷积神经网络(CNN)、生成对抗网络(GAN)、Transformer等深度学习技术,自动识别和分类农作物的病害,帮助农业工作者提高作物管理效率、减少损失。 1. 农作物病害检测的挑战…...

【C#】命名规范
文章目录 C# 命名规范使用Pascal case使用Camel case方法、属性、类命名见名知义LINQ查询变量使用有意义的名称如何声明成员变量和字段正确格式化和缩进代码如何撰写备注 通用C#编码最佳实践如何将值与空字符串进行比较使用异常处理使用&&和||可获得更好的性能单一职责…...

超级帐本(Hyperledger)
1. Hyperledger 项目 Hyperledger 下有两类项目:第一类是区块链框架项目;第二类是支持这些区块链的相关工具或模块。 在 Hyperledger 框架下,目前有 5 个区块链框架项目:Fabric、Sawtooth Lake、Iroha、Burrow 和 Indy。 在模块类下,则有 Hyp…...

如何精细优化网站关键词排名:实战经验分享
在数字营销日益激烈的今天,我深知每一个关键词的排名都关乎着网站的流量与转化。凭借多年的实战经验,我深刻体会到,要想在浩如烟海的网络世界中脱颖而出,精细化的关键词优化策略至关重要。今天,我将从实战角度出发&…...
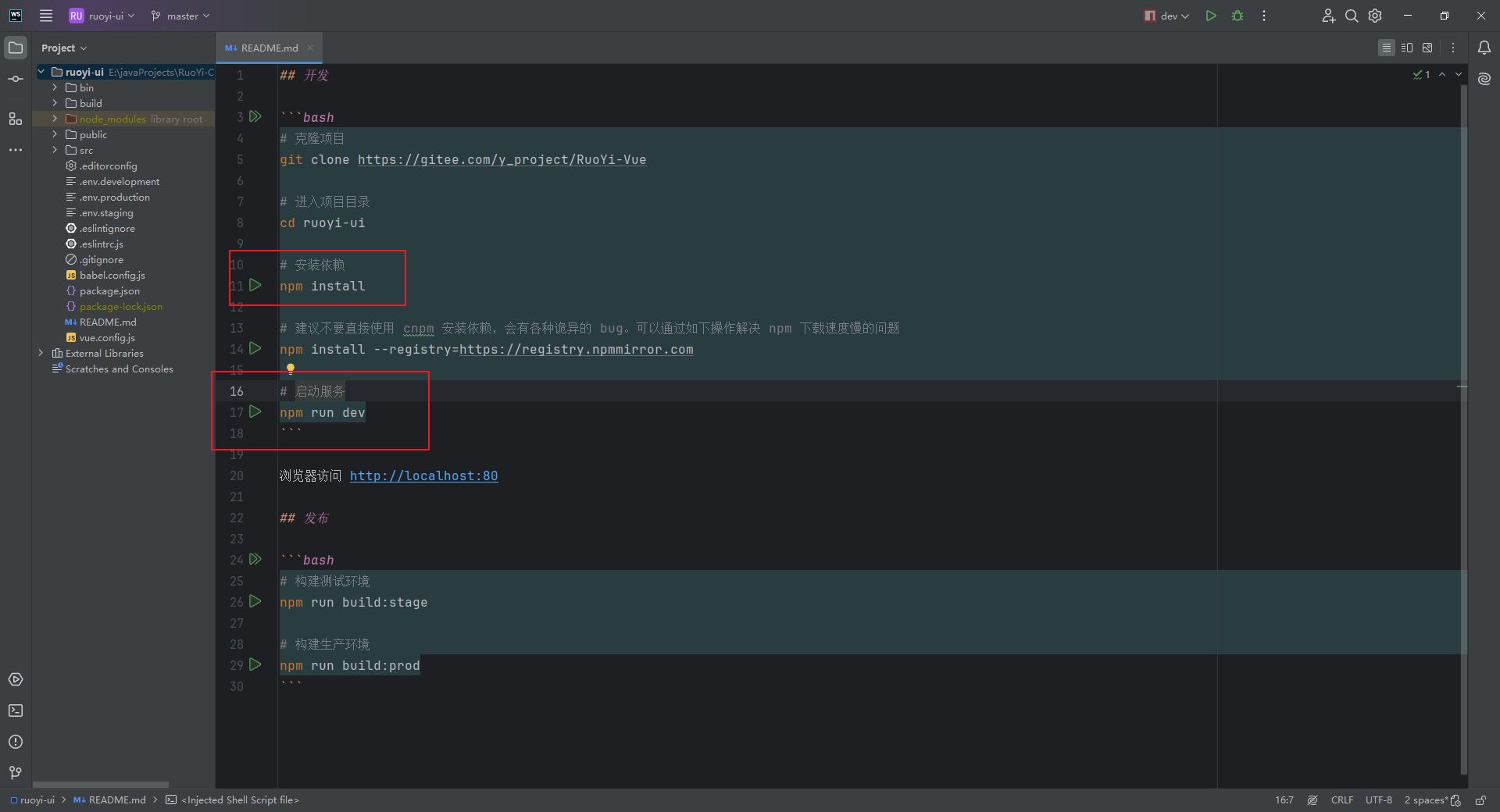
Ruoyi Cloud 本地启动
本文视频版本:https://www.bilibili.com/video/BV1SNtueBE9M 参考 http://doc.ruoyi.vip/ https://gitee.com/y_project/RuoYi-Cloud https://blog.csdn.net/cs_dnzk/article/details/135289966 https://doc.ruoyi.vip/ruoyi-cloud/cloud/seata.html#%E5%9F%BA%E6…...

Nginx解析:入门笔记
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》《MYSQL》 💪🏻 制定明确可量化的目标,坚持默默的做事。 ✨欢迎加入探索nginx之旅✨ 👋 大家好!文本学习和探索Nginx配置。…...
在 Mac 上安装双系统会影响性能吗,安装双系统会清除数据吗?
在 Mac 系统安装并使用双系统已经成为了许多用户办公的选择之一,双系统可以让用户在 Mac 上同时运行 Windows 或其他操作系统。然而,许多用户担心这样做会对 Mac 的性能产生影响。 接下来将给大家介绍 Mac 装双系统会影响性能吗,Mac装双系统…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
