【极限、数学】 NOIP 2018 提高组初赛试题 第 7 题详解(线段长度期望)

在一条长度为 1 1 1 的线段上随机取两个点,则以这两个点为端点的线段的期望长度是( )。
考虑将一个线段上平均分布有 n ( n ≥ 2 ) n(n\geq 2) n(n≥2) 个节点,其中首尾均有一个节点,那么我们就将一个线段均分为 n − 1 n-1 n−1 份。
不妨令第一个点取在第 i i i 个节点上,第二个点取在 j j j 上。不妨令 i ≤ j i \leq j i≤j,因为调换 i , j i,j i,j 对题意没有任何影响(显而易见)。
对于 i , j i,j i,j,我们共有 n ( n + 1 ) 2 \dfrac{n(n+1)}{2} 2n(n+1) 种取法。
假设 i = 1 i=1 i=1,则对于 j j j,长度总和为 ( n − 1 ) n 2 ( n − 1 ) \dfrac{(n-1)n}{2(n-1)} 2(n−1)(n−1)n
同理对于 i = 2 i=2 i=2,则总和为: ( n − 2 ) ( n − 1 ) 2 ( n − 1 ) \dfrac{(n-2)(n-1)}{2(n-1)} 2(n−1)(n−2)(n−1)。
因此对于所有 i i i,总和为: 0 × 1 + 1 × 2 + ⋯ + ( n − 1 ) n 2 ( n − 1 ) \dfrac{0\times1+1\times2+\dots+(n-1)n}{2(n-1)} 2(n−1)0×1+1×2+⋯+(n−1)n
证明:对于任意正整数 N N N,有 ∑ i = 1 N i ( i + 1 ) = N ( N + 1 ) ( N + 2 ) 3 \sum_{i=1}^{N}i(i+1) = \dfrac{N(N+1)(N+2)}{3} ∑i=1Ni(i+1)=3N(N+1)(N+2)。
考虑数学归纳法,对于 N = 1 N=1 N=1 显而易见等式成立。若 N N N 时成立,则对于 N + 1 N+1 N+1,有 ∑ i = 1 N + 1 i ( i + 1 ) = N ( N + 1 ) ( N + 2 ) 3 + ( N + 1 ) ( N + 2 ) = ( N + 1 ) ( N + 2 ) ( N + 3 ) 3 \sum_{i=1}^{N + 1}i(i+1) = \dfrac{N(N+1)(N+2)}{3} + (N+1)(N+2) = \dfrac{(N+1)(N+2)(N+3)}{3} ∑i=1N+1i(i+1)=3N(N+1)(N+2)+(N+1)(N+2)=3(N+1)(N+2)(N+3),因此如果当 N N N 成立, N + 1 N+1 N+1 时等式也成立,得证。
因此原式= ( n − 1 ) n ( n + 1 ) 6 ( n − 1 ) = n ( n + 1 ) 6 \dfrac{(n-1)n(n+1)}{6(n-1)} =\dfrac{n(n+1)}{6} 6(n−1)(n−1)n(n+1)=6n(n+1)
所以期望值: n ( n + 1 ) 6 n ( n + 1 ) 2 = 1 3 \dfrac{\dfrac{n(n+1)}{6}}{\dfrac{n(n+1)}{2}} = \dfrac{1}{3} 2n(n+1)6n(n+1)=31
原题即为:当 n n n 接近正无穷大时的期望值,显而易见也是 1 3 \dfrac{1}{3} 31。
相关文章:

【极限、数学】 NOIP 2018 提高组初赛试题 第 7 题详解(线段长度期望)
在一条长度为 1 1 1 的线段上随机取两个点,则以这两个点为端点的线段的期望长度是( )。 考虑将一个线段上平均分布有 n ( n ≥ 2 ) n(n\geq 2) n(n≥2) 个节点,其中首尾均有一个节点,那么我们就将一个线段均分为 n…...

《论网络安全体系设计》写作框架,软考高级系统架构设计师
论文真题 随着社会信息化的普及,计算机网络已经在各行各业得到了广泛的应用。目前,绝大多数业务处理几乎完全依赖计算机和网络执行,各种重要数据如政府文件、工资档案、财务账目和人事档案等均依赖计算机和网络进行存储与传输。另一方面&…...
这款开源的通用PDF处理神器,功能炸裂!
今天分享一款以PDF为中心的多功能办公学习工具箱软件,包含四大板块功能:PDF实用工具箱、Anki制卡神器、Anki最强辅助、视频笔记神器,软件功能众多且强大,熟练运用可以大幅提高办公和学习效率,绝对是您不可多得的效率神…...

RabbitMQ延迟消息——DelayExchange插件
什么是死信以及死信交换机 当一个队列中的消息满足下列情况之一时,可以成为死信: 1. 消费者使用basic.reject或 basic.nack声明消费失败,并且消息的requeue参数设置为false 2. 消息是一个过期消息,超时无人消费 3. 要投递的队列消…...

【系统规划与管理师】【案例分析】【考点】【答案篇】第5章 IT服务部署实施
【问题篇】☞【系统规划与管理师】【案例分析】【考点】【问题篇】第5章 IT服务部署实施 【移动端浏览】☞【系统规划与管理师】【案例分析】【模拟考题】章节考题汇总(第5章)(答案篇)(共24个知识点) 第5章…...

华为云服务器的数据库部署及管理
不管是终端数据上报到服务器进行存储,还是客户端的动态请求都需要用到数据库,因此这里对数据库的使用进行了一些记录,租用的是华为云的ECS弹性服务器(Ubuntu18)。下面以网页登录的账号信息Acount为例。 一、Mysql的安装…...
中连续几位(bit)的内容)
C#【必备技能篇】替换一个字节(byte)中连续几位(bit)的内容
文章目录 一、一个示例二、通用方法 一、一个示例 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;namespace ConsoleApp1 {class Program{static void Main(string[] args){Method1();}public static…...

roboguide将tp程序转化为LS文本格式的方法
不同的软件版本可能操作不同,但是仍然可以参考文章中的办法。 我使用的版本如图所示: 1.首先,打开任意一个工程,如果没有,可以打开自带的示例。 如图,我打开了自带的示例,在帮助文档中可以找到…...

基于SpringBoot+Vue+MySQL的流浪猫狗宠物救助救援网站管理系统
系统展示 用户前台界面 管理员后台界面 系统背景 在当今社会,随着宠物数量的激增及人们关爱动物意识的提升,流浪猫狗问题日益严峻。为解决这一问题,构建一套高效、便捷的流浪猫狗宠物救助救援网站管理系统显得尤为重要。本系统基于SpringBoot…...

I/O 多路复用:`select`、`poll`、`epoll` 和 `kqueue` 的区别与示例
I/O 多路复用是指在一个线程内同时监控多个文件描述符(File Descriptor, FD),以便高效地处理多个 I/O 事件。在 UNIX/Linux 和 BSD 系统中,select、poll、epoll、kqueue 都是实现 I/O 多路复用的系统调用。它们各有特点࿰…...

大数据之Flink(三)
9.3、转换算子 9.3.1、基本转换算子 9.3.1.1、映射map 一一映射 package transform;import bean.WaterSensor; import org.apache.flink.streaming.api.datastream.DataStreamSource; import org.apache.flink.streaming.api.datastream.SingleOutputStreamOperator; impor…...

【HCIA-Datacom】IPv4地址介绍
| | 👉个人主页:Reuuse 希望各位多多支持!❀ | 👉HCIA专栏博客 | 最后如果对你们有帮助的话希望有一个大大的赞! | ⭐你们的支持是我最大的动力!⭐ | 目录 IPv4地址定义IPv4地址分类方式二级目录三级目录 I…...

maven父子工程多模块如何管理统一的版本号?
1.为什么要统一管理? maven父子工程多模块,每个模块还都可以独立存在,子模块往往通常希望和父工程保持一样的版本,如果每个工程单独定义版本号,后期变更打包也非常麻烦,如何维护一个全局的版本号呢&#x…...

JavaScript --函数的作用域(全局和局部)
全局作用域 全局作用域,就算不在一个script标签也能调用 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta nam…...

贪吃蛇项目实现(C语言)——附源码
前言 贪吃蛇是一款十分经典的游戏,其通过控制贪吃蛇的上下左右移动来吃食物,延长自己的身体,也会因为撞到墙体和自身而死亡。下面我们通过C语言来实现贪吃蛇。 1.技术要点 C语言枚举,结构体,链表,动态内…...

【C++】42道面试经典问题总结
C this指针是干什么用的? 假如一个类型定义了很多对象,类里面有很多定义的私有成员变量,共享一套成员方法。通过this指针这可以区分方法、变量是操作的哪个对象的。 C的new和delete,new[]和delete[]可以混用吗? 一般来…...

php 实现JWT
在 PHP 中,JSON Web Token (JWT) 是一种开放标准 (RFC 7519) 用于在各方之间作为 JSON 对象安全地传输信息。JWT 通常用于身份验证系统,如 OAuth2 或基于令牌的身份验证。 以下是一个基本的 PHP 实现 JWT 生成和验证的代码示例。 JWT 的组成部分 JWT …...

vue table id一样的列合并
合并场景:如果id一样,则主表列合并,子表列不做合并,可实现单行、多行合并,亲测!!! 展示效果如图示: 组件代码: // table组件 :span-method"objectSpa…...
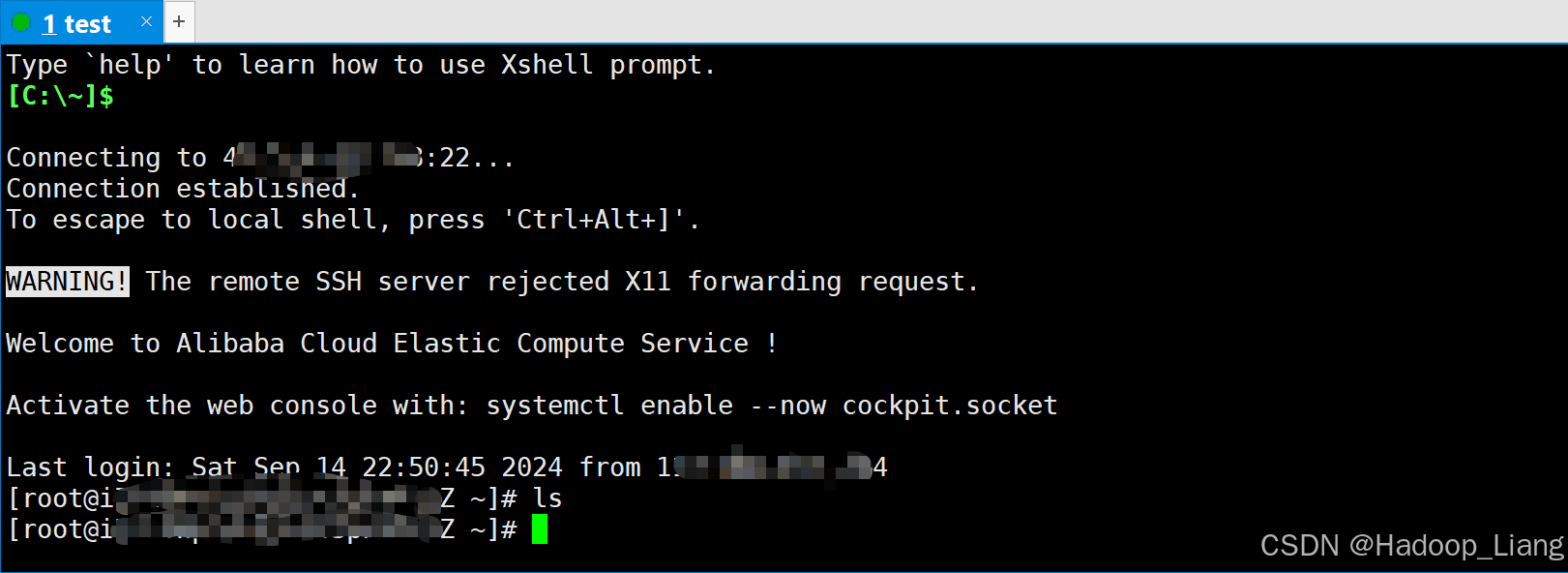
xshell密钥方式连接阿里云Linux
前提条件 有阿里云ECS linux实例安装好xshell工具 步骤 创建密钥对并绑定ECS实例 浏览器登录阿里云-->控制台-->ECS服务器-->网络与安全-->密钥对-->创建密钥对 根据提示填写密钥名称-->选中默认资源组-->创建 创建完成,会自动下载密钥对的…...

Wni11 下 WSL 安装 CentOS
Wni11 下 WSL 安装 CentOS 方法一、安装包安装下载包安装安装打开 CentOS1. 从 Windows 终端 打开2. 从 PowerShell 打开 方法二、导入 CentOS 的 tar 文件进行安装0. 查看版本(可选)1. 导出 Docker 容器到 tar 文件2. 将 tar 文件导入 WSL2.1. 导入 tar…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
