信息安全数学基础(14)欧拉函数
前言
在信息安全数学基础中,欧拉函数(Euler's Totient Function)是一个非常重要的概念,它与模运算、剩余类、简化剩余系以及密码学中的许多应用紧密相关。欧拉函数用符号 φ(n) 表示,其中 n 是一个正整数。
一、定义
欧拉函数 φ(n) 定义为小于或等于 n 的正整数中与 n 互质的数的个数。换句话说,如果 n 是一个正整数,那么 φ(n) 就是模 n 的简化剩余系中元素的个数。
二、性质
- 基本性质:
- φ(1)=1,因为1与任何数都互质。
- 如果 n 是素数 p,则 φ(p)=p−1,因为除了1以外的所有小于 p 的正整数都与 p 互质。
- 积性性质:
- 如果 m 和 n 是两个互质的正整数(即 gcd(m,n)=1),则 φ(mn)=φ(m)φ(n)。这个性质是欧拉函数最重要的性质之一,它允许我们将大数的欧拉函数计算分解为小数的欧拉函数计算。
- 其他性质:
- 如果 n=pk,其中 p 是素数,k 是正整数,则 φ(n)=pk−pk−1=pk−1(p−1)。这是因为除了 p 的倍数外,所有小于或等于 n 的正整数都与 n 互质。
- 对于任意正整数 n,都有 ∑d∣nφ(d)=n,其中 d∣n 表示 d 是 n 的正除数。这个性质是欧拉函数与除数函数的一个重要关系。
三、应用
密码学:在RSA加密算法中,公钥和私钥的生成涉及到选择两个大的互质素数 p 和 q,并计算它们的乘积 n=pq。在这个过程中,φ(n)=φ(pq)=(p−1)(q−1) 被用来计算公钥和私钥的模逆元。
数论:欧拉函数在数论中有许多应用,如求解同余方程、证明费马小定理和欧拉定理等。
组合数学:欧拉函数与组合数学中的一些问题也有关联,如计算有限域上多项式的根的个数等。
四、计算方法
直接计算:对于较小的 n,可以直接计算小于或等于 n 的正整数中与 n 互质的数的个数。
利用积性性质:对于较大的 n,如果 n 可以分解为若干个素数的幂的乘积,即 n=p1e1p2e2⋯pkek,则可以利用欧拉函数的积性性质计算 φ(n)=φ(p1e1)φ(p2e2)⋯φ(pkek)。
筛法:对于需要计算一系列连续整数的欧拉函数值的情况,可以使用筛法(如埃拉托斯特尼筛法的变种)来高效地计算。
![]() 结语
结语
珍惜眼前的每一刻
才能真正体验到生活的美好
!!!

相关文章:

信息安全数学基础(14)欧拉函数
前言 在信息安全数学基础中,欧拉函数(Eulers Totient Function)是一个非常重要的概念,它与模运算、剩余类、简化剩余系以及密码学中的许多应用紧密相关。欧拉函数用符号 φ(n) 表示,其中 n 是一个正整数。 一、定义 欧…...

7-17 汉诺塔的非递归实现
输入样例: 3输出样例: a -> c a -> b c -> b a -> c b -> a b -> c a -> c 分析: 不会汉罗塔的uu们,先看看图解: 非递归代码: #include<iostream> #include<stack> using namespace std; s…...

word文档无损原样转pdf在windows平台使用python调用win32com使用pip安装pywin32
前提: windows环境下,并且安装了office套装,比如word,如果需要调用excel.也需要安装。在另外的文章会介绍。这种是直接调用word的。所以还原度会比较高。 需求: word文档转pdf,要求使用命令行形式,最终发布为api接口…...

海康威视相机在QTcreate上的使用教程
文章目录 前言:基础夯实:效果展示:图片展示:视频展示: 参考的资料:遇到问题:问题1:int64 does not问题2:LNK2019配置思路(这个很重要)配置关键图片:配置具体过…...
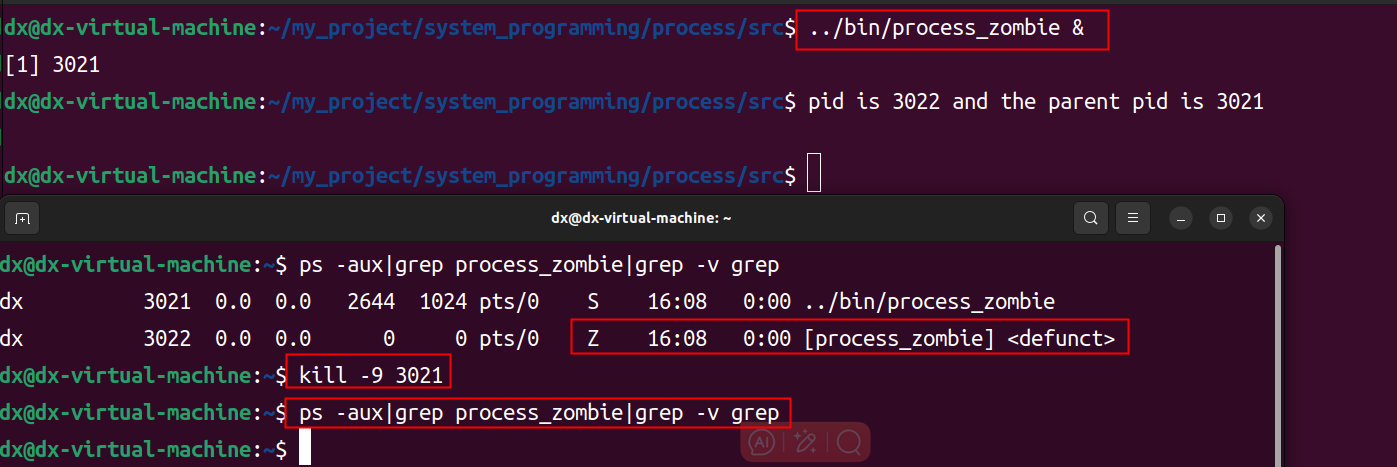
进程状态、进程创建和进程分类
文章目录 进程进程常见的状态进程调度进程状态变化关系 进程标识示例--进程标识的使用以及简介 进程创建fork函数vfork函数示例--使用fork函数创建子进程,并了解进程之间的关系 创建进程时发生的变化虚拟内存空间的变化示例--验证fork函数创建进程时的操作 对文件IO…...

java后端请求调用三方接口
java后端请求调用三方接口 /*** param serverURL http接口地址(例:http://www.iwsu.top:8016/dataSyn/bay/statsCar)* param parm 参数(可以是json,也可以是json数组)*/ public void doRestfulPostBody(St…...
)
C#使用TCP-S7协议读写西门子PLC(三)
接上篇 C#使用TCP-S7协议读写西门子PLC(二)-CSDN博客 这里我们进行封装读写西门子PLC的S7协议命令以及连接西门子PLC并两次握手 新建部分类文件SiemensS7ProtocolUtil.ReadWrite.cs 主要方法: 连接西门子PLC并发送两次握手。两次握手成功后,才真正连…...

铝型材及其常用紧固件、连接件介绍
铝型材介绍(包括紧固件和连接件以及走线) 铝型材 铝型材一般是6063铝合金挤压成型,分为欧标和国标两个标准。(左边国标,右边欧标,欧标槽宽一点) 由于槽型不一样,相关的螺栓和螺母也…...
-安装开发所需工具)
【裸机装机系列】7.kali(ubuntu)-安装开发所需工具
如果你是后端或是人工智能AI岗,可以安装以下推荐的软件: 1> sublime sublime官网 下载deb文件 安装命令 sudo dpkg -i sublime-text_build-4143_amd64.deb2> vscode 安装前置软件 sudo apt install curl gpg software-properties-common apt-t…...

[C语言]第九节 函数一基础知识到高级技巧的全景探索
目录 9.1 函数的概念 9.2 库函数 9.2.1 标准库与库函数 示例:常见库函数 9.2.2 标准库与头文件的关系 参考资料和学习工具 如何使用库函数 编辑 9.3 ⾃定义函数 9.3.1 函数的语法形式 9.3.2函数的举例 9.4 实参与形参 9.4.1 什么是实参? 9…...

1.1 计算机网络基本概述
欢迎大家订阅【计算机网络】学习专栏,开启你的计算机网络学习之旅! 文章目录 前言一、网络的基本概念二、集线器、交换机和路由器三、互连网与互联网四、网络的类型五、互连网的组成1. 边缘部分2. 核心部分 六、网络协议 前言 计算机网络是现代信息社会…...

Linux环境基础开发工具使用(gcc/g++与makefile)
1.Linux编译器-gcc/g使用 1. 背景知识 接下来的操作,我以gcc为例,因为两者选项都是通用的,所以也就相当于间接学习了 1.预处理(进行宏替换) 2.编译(生成汇编) 3.汇编(生成机器可识别代码)…...
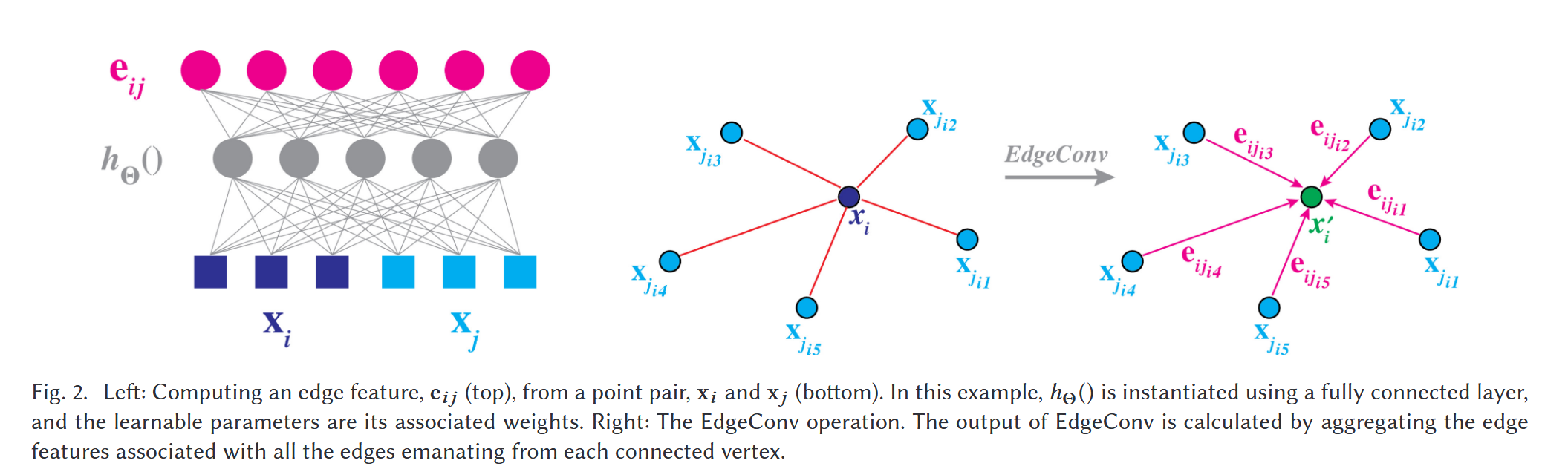
PointNet++改进策略 :模块改进 | EdgeConv | DGCNN, 动态图卷积在3d任务上应用
目录 介绍核心思想及其实现核心思想实现步骤 如何改进PointNet**局部几何结构的处理****动态图的引入****特征聚合的灵活性****全局和局部特征的结合** 论文题目:Dynamic Graph CNN for Learning on Point Clouds发布期刊:TOG作者单位:麻省理…...

FFmpeg源码:skip_bits、skip_bits1、show_bits函数分析
GetBitContext结构体和其相关的函数分析: FFmpeg中位操作相关的源码:GetBitContext结构体,init_get_bits函数、get_bits1函数和get_bits函数分析 FFmpeg源码:skip_bits、skip_bits1、show_bits函数分析 一、skip_bits函数 skip…...

加密
一、加密 加密运算需要两个输入:密钥和明文 解密运算也需要两个输入:密钥和密文 密文通常看起来都是晦涩难懂、毫无逻辑的,所以我们一般会通过传输或者存储密文来保护私密数据,当然,这建立在一个基础上,…...

Kibana:如何使用魔法公式创建具有影响力的可视化效果?(第 1 部分)
作者:来自 Elastic Vincent du Sordet 我们将看到 Kibana Lens 编辑器中的神奇数学公式如何帮助突出显示高值。 简介 在上一篇博文《作为非设计师设计直观的 Kibana 仪表板》中,我们强调了创建直观仪表板的重要性。它展示了简单的更改(分组…...

【C++】多态and多态原理
目录 一、多态的概念 二、多态的定义及实现 🌟多态的构成条件 🌟虚函数 🌟虚函数的重写 🌠小贴士: 🌟C11 override 和 final 🌟重载、重写(覆盖)、重定义…...

C# 实现二维数据数组导出到 Excel
目录 功能需求 范例运行环境 Excel DCOM 配置 设计实现 组件库引入 编辑 方法设计 生成二维数据数组 核心方法实现 调用示例 总结 功能需求 将数据库查询出来的数据导出并生成 Excel 文件,是项目中经常使用的一项功能。本文将介绍通过数据集生成二维…...
nlohmann::json中有中文时调用dump转string抛出异常的问题
问题描述 Winodows下C开发想使用一个json库,使用的nlohmann::json,但是遇到json中使用中文时,转成string,会抛出异常。 nlohmann::json contentJson;contentJson["chinese"] "哈哈哈";std::string test con…...

Unity中InputField一些属性的理解
先看代码: using UnityEngine; using UnityEngine.UI;public class TestInput : MonoBehaviour {[SerializeField]InputField inputField;void Start(){Debug.Log(inputField.text);Debug.Log(inputField.text.Length);Debug.Log(inputField.preferredWidth);Debug…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
