【Java】关键字-static【主线学习笔记】
文章目录
- 前言
- 关键字:static
- 静态变量
- 静态方法
- 设置为静态的场景
- 下一篇
前言
Java是一门功能强大且广泛应用的编程语言,具有跨平台性和高效的执行速度,广受开发者喜爱。在接下来的学习过程中,我将记录学习过程中的基础语法、框架和实践技巧等,分享学习心得,对自己学习过程进行整理和总结,也希望能为其他学习Java的朋友提供一些帮助和参考。
关键字:static
在Java中,实例变量(未被static修饰的变量)是每个实例对象独有的,每个对象都有属于自己的一份实例变量。如果希望某个成员变量能够被类的所有实例共享,可以使用static关键字进行修饰,这样的变量称为类变量。
static关键字的主要作用是用于定义类级别的属性和方法。静态成员在类加载时就会被初始化,并且能够被所有实例共享。静态成员在需要共享资源、提高性能以及定义常量时非常有用。
静态变量
- 适用于需要被所有实例共享的变量,例如计数器、配置参数等。
/**
*每创建一个Counter对象,count都会增加,但这个值对所有Counter实例都是共享的。
**/
class Counter {static int count = 0; // 静态变量,所有对象共享Counter() {count++;}
}静态方法
随着类的加载而加载,可以通过“类.静态方法”的方式,直接调用静态方法。
常用于工具类或不涉及实例数据的操作。
/**
*可以直接通过MathUtil.add(3, 5)调用,而不需要创建MathUtil的实例。
**/
class MathUtil {static int add(int a, int b) {return a + b;}
}-静态方法内可以调用静态的属性或者静态的方法,但不可以调用非静态的结构(如非静态的属性、方法 )
设置为静态的场景
- 判断当前类的多个实例是否能够共享此成员变量。
- 开发中常将一些常量声明为静态的
- 方法内操作的变量都是静态变量的话,就推荐将该方法声明为静态方法
- 开发中,常将工具中的方法,声明为静态方法
下一篇
【Java】类的成员之一-代码块【主线学习笔记】
相关文章:

【Java】关键字-static【主线学习笔记】
文章目录 前言关键字:static静态变量静态方法设置为静态的场景 下一篇 前言 Java是一门功能强大且广泛应用的编程语言,具有跨平台性和高效的执行速度,广受开发者喜爱。在接下来的学习过程中,我将记录学习过程中的基础语法、框架和…...
数字自然资源领域的实现路径
在数字化浪潮的推动下,自然资源的管理与利用正经历着前所未有的变革。本文将从测绘地理信息与遥感专业的角度,深度分析数字自然资源领域的实现路径。 1. 基础数据的数字化 数字自然资源的构建,首先需要实现基础数据的数字化。这包括地形地貌…...

GitLab邮箱发送邮件:如何实现自动化发信?
gitlab邮箱发送邮件设置教程?Gitlab邮箱配置和使用? GitLab不仅提供了代码版本控制、持续集成/持续部署等功能,还支持通过其内置的邮件功能实现自动化邮件发送。AokSend将深入探讨如何在GitLab中配置和使用邮箱发送邮件功能。 GitLab邮箱发…...
sqli-labs靶场搭建
下载了一个phpstudy进行搭靶场搭建 然后打开phpstudy安装好php,mysql等环境 正式sqli-labs靶场搭建 第一步:下载源码:https://codeload.github.com/Audi-1/sqli-labs/zip/master 解压后放进网站根目录,进到 sqli-labs的文件夹下࿰…...

Leetcode Hot 100刷题记录 -Day14(矩阵置0)
矩阵置0 问题描述: 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:…...

每日刷题(算法)
我们N个真是太厉害了 思路: 我们先给数组排序,如果最小的元素不为1,那么肯定是吹牛的,我们拿一个变量记录前缀和,如果当前元素大于它前面所有元素的和1,那么sum1是不能到达的值。 代码: #def…...

大牛直播SDK核心音视频模块探究
技术背景 视沃科技旗下”大牛直播SDK”,始于2015年,致力于传统行业极致体验的音视频直播技术解决方案,产品涵盖跨平台的实时RTMP推流、RTMP/RTSP直播播放(支持RTSP|RTMP H.265,Enhanced RTMP H.265)、GB28181设备接入、推送端播放…...

gin配置swagger文档
一、基本准备工作 1、安装依赖包 go get -u github.com/swaggo/swag/cmd/swag go get -u github.com/swaggo/gin-swagger go get -u github.com/swaggo/files2、在根目录上配置swagger的路由文件 //2.初始化路由router : initialize.Routers()// 配置swaggerdocs.SwaggerInfo…...

基于ssm的快餐店点餐系统设计与实现
需要项目源码请联系我,目前有各类成品 毕设 javaweb ssh ssm springboot等等项目框架,源码丰富。 专业团队,咨询就送开题报告,活动限时免费,有需要的朋友可以来留言咨询。 一、摘要 进入二十一世纪以来,计…...

集合框架底层使用了什么数据结构
1.是什么 集合框架(Collection Framework)是Java标准库的一部分,它提供了一系列接口和实现类,用于处理不同类型的集合。这些集合可以用于存储和操作对象,如列表、集合、映射等。集合框架的底层数据结构是多种多样的&am…...
Activiti7《第二式:破剑式》——工作流中的以柔克刚
冲冲冲!开干 这篇文章将分为九个篇章,带你逐步掌握工作流的核心知识。这篇文章将带你深入探讨工作流中的 “破剑式”,揭示如何通过 柔与刚 的结合来破解工作流的复杂性。本篇包含了 Activiti7 环境的进一步优化和表结构的深入分析࿰…...

docker快速搭建kafka
1、拉取镜像 kafka和 zk镜像 docker pull wurstmeister/zookeeper docker pull wurstmeister/kafka:1.1.02、运行zk容器 docker run -itd --restart always --name zookeeper -p 2181:2181 wurstmeister/zookeeper3、运行kafka容器 192.168.31.112 这个地址为zk地址 docker…...
基于 onsemi NCV78343 NCV78964的汽车矩阵式大灯方案
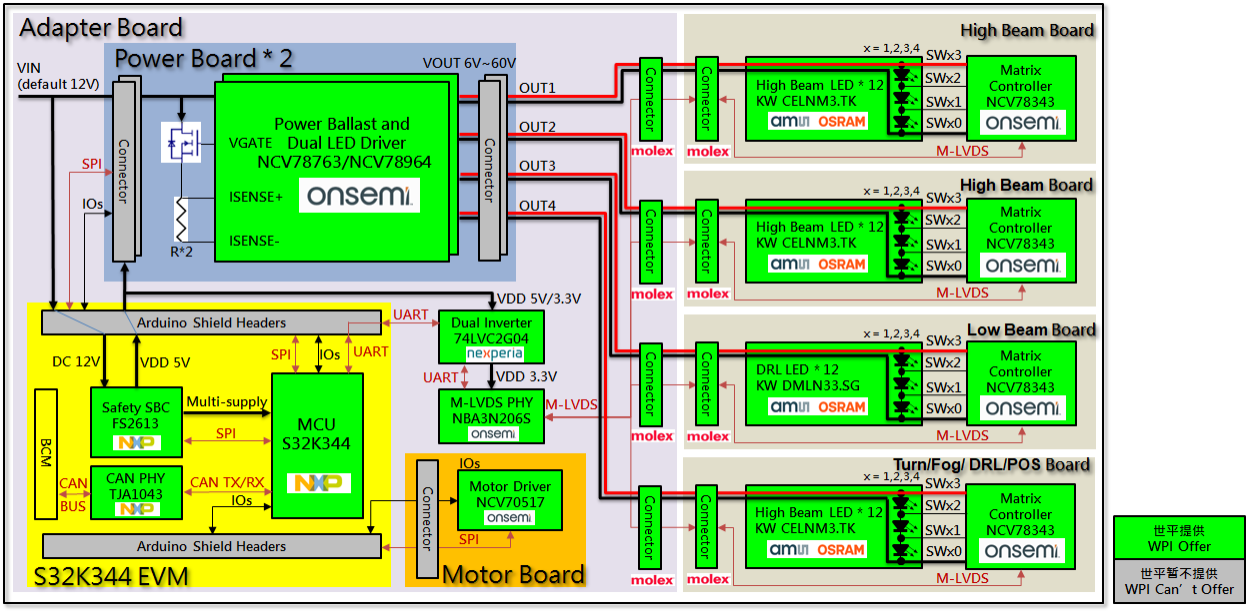
一、方案描述 大联大世平集团针对汽车矩阵大灯,推出 基于 onsemi NCV78343 & NCV78964的汽车矩阵式大灯方案。 开发板搭载的主要器件有 onsemi 的 Matrix Controller NCV78343、LED Driver NCV78964、Motor Driver NCV70517、以及 NXP 的 MCU S32K344。 二、开…...

OpenAl o1论文:Let’s Verify Step by Step 快速解读
OpenAl又火了,这次是o1又带给大家惊艳。网上的博主已经有了真真假假的各种评测,我这篇来一点硬核的,解读OpenAl o1背后的论文:Let’s Verify Step by Step 大模型在给定的上下文资料正确的情况下也有可能出现幻觉,这篇…...

Errorresponsefromdaemon:toomanyrequests:Youhavereachedyourpullratelimit.
Errorresponsefromdaemon:toomanyrequests:Youhavereachedyourpullratelimit.Youmayincreasethelimitbyauthenticatingandupgrading:https://www.docker.com/increase−rate−limit.See ′ dockerrun−−help 在拉取docker进行的时候遇到这个问题,如何解决呢?本文提供的解决方…...

[2025]医院健康陪诊系统(源码+定制+服务)
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…...

Golang | Leetcode Golang题解之第405题数字转换为十六进制数
题目: 题解: func toHex(num int) string {if num 0 {return "0"}sb : &strings.Builder{}for i : 7; i > 0; i-- {val : num >> (4 * i) & 0xfif val > 0 || sb.Len() > 0 {var digit byteif val < 10 {digit 0…...
)
VB中如何使用正则表达式(Regular Expressions)
在Visual Basic (VB) 中使用正则表达式,你需要依赖于.NET Framework的System.Text.RegularExpressions命名空间。这个命名空间提供了一系列的类,其中最常用的是Regex类,它允许你在VB.NET中执行复杂的文本搜索和替换操作。 以下是如何在VB.NE…...

Docker FROM 指定基础镜像
所谓定制镜像,其一定是以一个镜像为基础,在其上进行定制。 比如一个 nginx 镜像的容器,再进行修改一样,基础镜像是必须指定的。而 FROM 就是指定基础镜像,因此一个 Dockerfile 中 FROM 是必备的指令,并且必…...

19:I2C一:程序模拟I2C通信时序
I2C 1、什么是I2C2、I2C的通信时序2.1:起始信号2.2:停止信号2.3:主机向从机发送一个字节数据2.4:主机向从机读取一个字节数据2.5:主机接收应答2.6:主机发送应答 3、程序模拟I2C的通信时序3.1:指…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
