蓝桥杯刷题冲刺 | 倒计时10天
作者:指针不指南吗
专栏:蓝桥杯倒计时冲刺🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾
文章目录
- 1.有边数限制的最短路
- 2.九进制转十进制
1.有边数限制的最短路
-
题目
链接: 853. 有边数限制的最短路 - AcWing题库
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 11 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出
impossible。注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
点的编号为 1∼n。
输出格式
输出一个整数,表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
如果不存在满足条件的路径,则输出
impossible。数据范围
1≤n,k≤500,
1≤m≤10000,
1≤x,y≤n,
任意边长的绝对值不超过 10000。输入样例:
3 3 1 1 2 1 2 3 1 1 3 3输出样例:
3 -
我的题解
#include<bits/stdc++.h> using namespace std;const int N=510,M=10010;int n,m,k; int dist[N]; int backup[N];struct node{int a,b,c; }g[N];int Bellman() {memset(dist,0x3f,sizeof dist);dist[1]=0;for(int i=0;i<k;i++){memcpy(backup,dist,sizeof dist);for(int j=0;j<m;j++){int a=g[j].a,b=g[j].b,w=g[j].c;dist[b]=min(dist[b],backup[a]+w);}}if(dist[n]>0x3f3f3f3f/2) return 0x3f3f3f3f/2+1;return dist[n]; }int main() {scanf("%d%d%d",&n,&m,&k);for(int i=0;i<m;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);g[i]={a,b,c};}int t=Bellman();if(t>0x3f3f3f3f/2) puts("impossible");else cout<<t; return 0; }
2.九进制转十进制
-
题目
链接: 九进制转十进制 - 蓝桥云课 (lanqiao.cn)
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
九进制正整数 (2022)9_99 转换成十进制等于多少?
-
我的题解1 AC 100%
#include<bits/stdc++.h> using namespace std;int main() {string s="2022";int x=stoi(s,0,9); //将n进制的字符串转化为十进制cout<<x;return 0; } -
我的题解2 ——第一次 AC 0%
#include<bits/stdc++.h> using namespace std;int main() {int n=2022;int res=0;while(n>0){int t=n%10;n/=10;res=res*9+t;cout<<res<<endl; }cout<<res;return 0; }这样计算的话,就反了,计算的是 2202的十进制
第二次 AC 100%
#include<bits/stdc++.h> using namespace std;int main() {string s="2022";int res=0;for(int i=0;i<=s.size()-1;i++) //借助于字符串{res=res*9+s[i]-'0';}cout<<res;return 0; } -
反思
进制转化问题:
- 填空题直接借助于计算器
- 编程,注意累乘的进位的顺序,别整反了;使用字符串来储存数字
- '0’是字符0的意思,他所对应的ASCII码为48;而0是数字0,ASCII中的0
-
ASCII 转换公式
ps 补充一下,以防以后遇到0-9 A-Z a-z ASCII码值 48-57 65-90 97-122 - ASCII码值大小:数字<大写字母<小写字母
- 以上三种ASCII码因为都是连续的,所以都可以加相应的数从而得到之后的ASCII码值
- 小写转大写:小写字母 - ‘a’ + ‘A’
- 大写转小写:大写字母 - ‘A’ + ‘a’
- 小写转数字:小写字母 - ‘a’ + ‘0’
- 原值减去 原对应类型的第一个值 (置零);
- 然后加上 所求类型的第一个值的ASCII。

相关文章:

蓝桥杯刷题冲刺 | 倒计时10天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.有边数限制的最短路2.九进制转十进制1.有边数限制的最短路 题目 链接: 853. 有边数…...

个人练习-Leetcode-剑指 Offer II 109. 开密码锁
题目链接:https://leetcode.cn/problems/zlDJc7/ 题目大意:给出一个四位数字的密码锁,初始状态是0000,目标是targer。每一次转动只能让一个位的轮盘转动一下(0往后转是9)。有一个vector<string> dea…...

四个常见的Linux面试问题
四个常见的Linux面试问题。 刚毕业要找工作了,只要是你找工作就会有面试这个环节,那么在面试环节中,有哪些注意事项值得我的关注呢?特别是专业技术岗位,这样的岗位询问一般都是在职的工程师,如何在面试环节…...

15、接口(C#)
15.1 什么是接口 接口是指定一组函数成员而不实现它们的引用类型。所以只能类和结构实现接口。 15.2 声明接口 接口声明不能包含以下成员 数据成员静态成员 接口声明只能包含以下类型的费静态成员函数声明: 方法事件索引器属性 这些函数成员的声明不能包含任何实…...
)
C++中常见的容器类使用方法举例(vector、deque、map、set)
cpp中常见的容器类有vector、list、deque、map、set、unordered_map和unordered_set。 下面将举例直接说明各个容器的使用方法。 文章目录综合示例1. vector:动态数组,支持随机访问2. list:双向链表,支持双向遍历和插入删除3. de…...
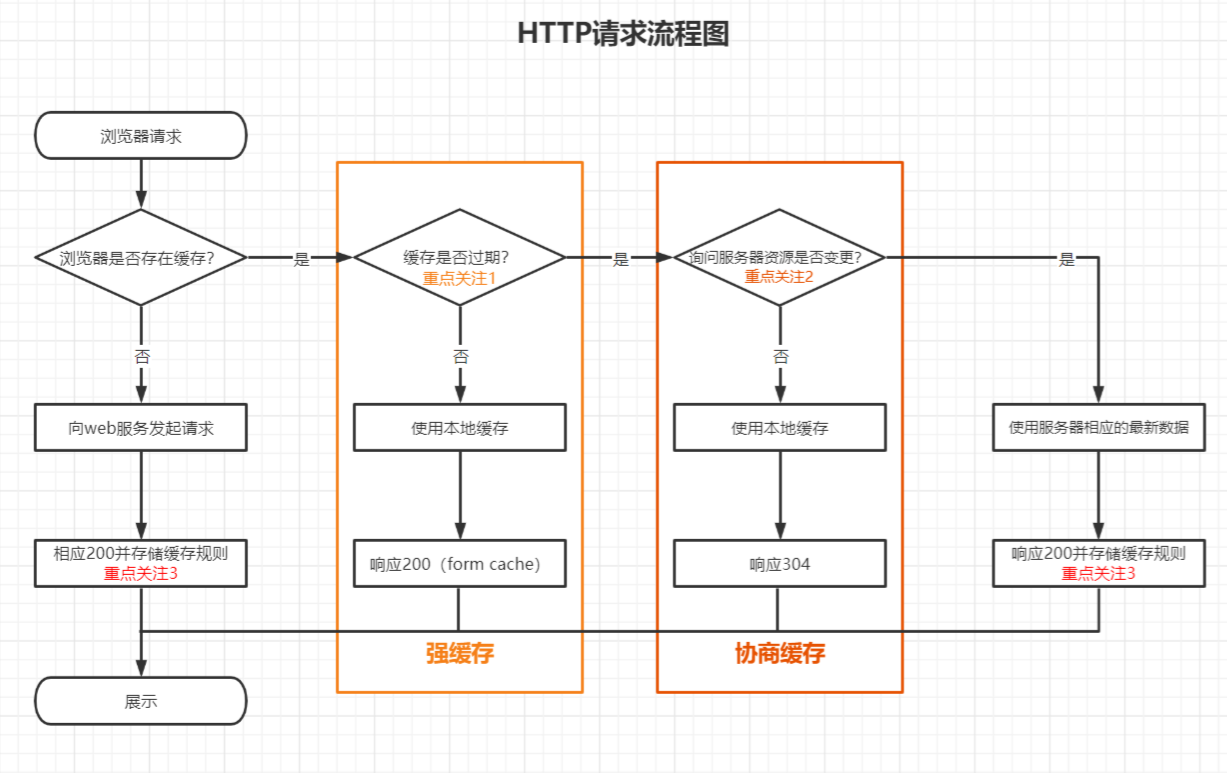
什么是强缓存和协商缓存
什么是缓存 浏览器缓存就是把一个已经请求过的Web资源(如html页面,图片,js,数据等)拷贝一份副本储存在浏览器中。缓存会根据进来的请求保存输出内容的副本。当下一个请求来到的时候,如果是相同的URL&#…...

算法刷题之堆
1. heapq 堆 Python 中只有最小堆: import heapqa [] heapq.heappush(a, 3) # 添加元素 heapq.heappush(a, 2) heapq.heappush(a, 1) while len(a): # 判断堆的长度print(heapq.heappop(a)) # 弹出堆顶元素# 将列表转换为最小堆 nums [2, 3, 1, 4, 5, 6] hea…...
javaweb导师选择系统
本文以JSP为开发技术,实现了一个导师选择系统。导师选择系统分为三大模块,包括管理员:学员信息管理、导师信息管理、导师选择管理、导师分布图、公告信息管理、系统管理,学生:个人资料管理、导师选择管理、导师分布图管…...

LeetCode150 逆波兰表达式求值
题目: 给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。 注意: 有效的算符为 ‘’、‘-’、‘*’ 和 ‘/’ 。每个操作数(运算对象)都可以…...
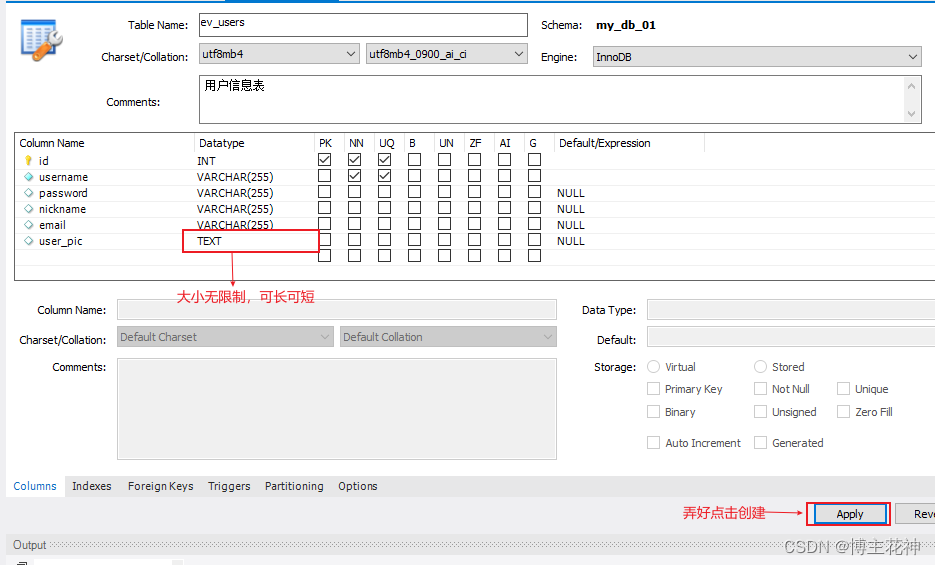
【Node.js】项目开发实战(中)
开发用户的注册和登录接口步骤1,打开MySQL Workbench,打开自己的数据库进入创建用户信息表新建 ev_users表安装并配置mysql模块安装mysql模块新建db文件夹下index.js,导入并配置mysql模块安装bcryptjs对密码进行加密处理新建/router_handler/user.js中&a…...

记录一次 New Bing 英语陪练
记录一次 New Bing 英语陪练 Now I start to speak english to chat with you . Help me find the mistake in my word and help me improve my english I’m glad you want to practice your English with me. I can help you find the mistakes in your words and help you i…...

【Python】照片居然能变素描?不会画画但是咱会代码
文章目录前言一、准备二、下载预训练模型总结前言 Photo-Sketching 一个能将照片的轮廓识别出来并将其转化为“速写”型图像的开源模块。 比如,这只小狗: 经过模型的转化,会变成卡通版的小狗: 非常秀,这很人工智能…...
已解决正确配置git环境变量
已解决git没有配置环境变量,抛出异常ERROR: Cannot find command ‘git’- do you have ‘git’ installed and in your PATH?,附上正确配置git环境变量的教程 文章目录报错问题报错翻译报错原因解决方法《100天精通Python》专栏推荐白嫖80g Python全栈…...

【逐步剖C】-第十章-自定义类型之结构体、枚举、联合
一、结构体 前言:有关结构体的声明、定义、初始化以及结构体的传参等结构体的基本使用在文章【逐步剖C】-第六章-结构体初阶中已进行了详细的介绍,需要的朋友们可以看看。这里主要讲解的是有关结构体的内存问题。 1. 结构体的内存对齐 (1&…...
Windows Server 2016 中文版、英文版下载 (updated Mar 2023)
Windows Server 2016 Version 1607,2023 年 3 月更新 请访问原文链接:https://sysin.org/blog/windows-server-2016/,查看最新版。原创作品,转载请保留出处。 作者主页:sysin.org 本站将不定期发布官方原版风格月度更…...

Linux 4G 通信实验
目录4G 网络连接简介高新兴ME3630 4G 模块实验ME3630 4G 模块简介ME3630 4G 模块驱动修改ME3630 4G 模块ppp 联网测试前面我们学习了如何在Linux 中使用有线网络或者WIFI,但是使用有线网络或者WIFI 有 很多限制,因为要布线,即使是WIFI 你也得…...
华为OSPF技术详细介绍,保姆级,谁都能看懂(一)
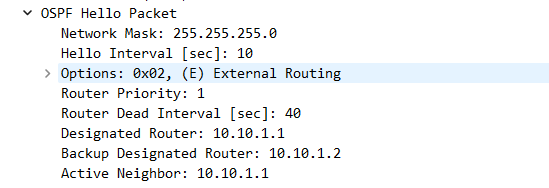
目录 1、简介 2、OSPF基本原理 3、OSPF的特点 4、OSPF区域 5、路由器的类型 6、OSPF5种报文 7、后半部分内容 1、简介 OSPF(Open Shortest Path First,开放最短路径优先)是一个基于链路状态的内部网关协 议。目前针对IPv4协议使用的是OS…...

行人车辆检测与计数系统(Python+YOLOv5深度学习模型+清新界面)
摘要:行人车辆检测与计数系统用于交通路口行人及车辆检测计数,道路人流量、车流量智能监测,方便记录、显示、查看和保存检测结果。本文详细介绍行人车辆检测,在介绍算法原理的同时,给出Python的实现代码、PyQt的UI界面…...

SM3哈希算法的FPGA实现 I
SM3哈希算法的FPGA实现 I SM3哈希算法的FPGA实现 I一、什么是SM3哈希算法?二、SM3哈希算法的具体内容1、填充2、迭代与压缩3、计算拼凑值三、参考文档语言 :verilog 仿真工具: Modelsim EDA工具:quartus II 一、什么是SM3哈希算法…...
【数据结构与算法】线性表--数组
文章目录一、前言二、数组的概念三、数组的操作数组的插入数组的删除四、容器与数组五、问题:为何数组要从0开始编号,而不是1开始呢?六、总结一、前言 常见的数据结构如下图,本文主要讲解数据结构线性表--数组。 二、数组的概念 …...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
