线性代数——行列式
文章目录
- 版权声明
- 排列
- 行列式
- 行列式的由来
- 行列式的概念
- 行列式的性质
- 重要公式
- 克拉默法则
- 补充知识
版权声明
本文大部分内容皆来自李永乐老师考研教材和视频课。
排列
由1,2,…,n1,2,\ldots,n1,2,…,n组成的有序数组称为一个nnn阶排列,通常使用j1j2…jnj_1j_2\ldots j_nj1j2…jn表示nnn阶排列。例如:
j1j2j3j4=9527j_1j_2j_3j_4=9527j1j2j3j4=9527
在排列中,如果一个大的数排在了一个小的数前面,就称这两个数构成了一个逆序。一个排列逆序的总数称为这个排列的逆序数。通常用τ(j1j2…jn)\tau(j_1j_2\ldots j_n)τ(j1j2…jn)表示排列j1j2…jnj_1j_2\ldots j_nj1j2…jn的逆序数。例如:
τ(9527)=4\tau(9527)=4τ(9527)=4
- 如果一个排列的逆序数是偶数,则称这个排列是偶排列。
- 如果一个排列的逆序数是奇数,则称这个排列是奇排列。
对换是指交换排列中任意两个元素的位置。
- 如果对一个排列进行奇数次对换那么将改变排列的奇偶性。
- 如果对一个排列进行偶数次对换那么将不会改变排列的奇偶性。
一个nnn阶排列经过对换可以得到n!n!n!个不同的排列,并且在这n!n!n!个不同的排列中,奇偶排列各占一半。
行列式
行列式的由来
现有一二元一次方程组:
{a1x+b1y=c1(1)a2x+b2y=c2(2)\begin{cases} a_1x+b_1y=c_1(1)\\ a_2x+b_2y=c_2(2) \end{cases}{a1x+b1y=c1(1)a2x+b2y=c2(2)
欲求xxx,由(1)×b2−(2)×b1(1)\times b_2-(2)\times b_1(1)×b2−(2)×b1得:
(a1b2−a2b1)x=c1b2−c2b1(a_1b_2-a_2b_1)x=c_1b_2-c_2b_1(a1b2−a2b1)x=c1b2−c2b1
在研究方程组求解的过程中数学家发现两个数相乘减两个数相乘是回避不掉的,于是数学家将这一过程单独提炼出来并写成以下形式:
∣a1b1a2b2∣x=∣c1b1c2b2∣\begin{vmatrix} a_1&b_1\\ a_2&b_2 \end{vmatrix}x= \begin{vmatrix} c_1&b_1\\ c_2&b_2 \end{vmatrix} a1a2b1b2x=c1c2b1b2
当
∣a1b1a2b2∣=a1b2−a2b1≠0\begin{vmatrix} a_1&b_1\\ a_2&b_2 \end{vmatrix}=a_1b_2-a_2b_1\neq0 a1a2b1b2=a1b2−a2b1=0
时xxx有唯一解:
x=∣c1b1c2b2∣∣a1b1a2b2∣x=\frac{\begin{vmatrix} c_1&b_1\\ c_2&b_2 \end{vmatrix}}{\begin{vmatrix} a_1&b_1\\ a_2&b_2 \end{vmatrix}} x=a1a2b1b2c1c2b1b2
那么就将∣abcd∣\begin{vmatrix}a&b\\c&d\end{vmatrix}acbd这种形式的数称为行列式。
行列式的概念
行列式是不同行不同列nnn个元素乘积的代数和:
∣A∣=∣a11a12…a1na21a22…a2n⋮⋮⋮an1an2…ann∣=∑j1j2…jn(−1)τ(j1j2…jn)a1j1a2j2…anjn|A|=\begin{vmatrix}a_{11} &a_{12}&\ldots&a_{1n}\\a_{21} &a_{22}&\ldots&a_{2n}\\\vdots&\vdots&&\vdots&\\a_{n1}&a_{n2}&\ldots&a_{nn}\end{vmatrix}=\sum_{j_1j_2\ldots j_n}(-1)^{\tau(j_1j_2\ldots j_n)}a_{1j_1}a_{2j_2}\dots a_{nj_n} ∣A∣=a11a21⋮an1a12a22⋮an2………a1na2n⋮ann=j1j2…jn∑(−1)τ(j1j2…jn)a1j1a2j2…anjn
这个式子称为行列式∣A∣|A|∣A∣的nnn阶完全展开式,共有n!n!n!项。
- 对于二阶三阶行列式有对角线法则:
- 2阶行列式:∣abcd∣=ad−bc\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bcacbd=ad−bc
- 3阶行列式:
∣a1a2a3b1b2b3c1c2c3∣=a1b2c3+a2b3c1+a3b1c2−a3b2c1−a2b1c3−a1b3c2\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}=a_1b_2c_3+a_2b_3c_1+a_3b_1c_2-a_3b_2c_1-a_2b_1c_3-a_1b_3c_2 a1b1c1a2b2c2a3b3c3=a1b2c3+a2b3c1+a3b1c2−a3b2c1−a2b1c3−a1b3c2
- 行列式的转置:转置是指将行列式的行和列互换。行列式∣A∣|A|∣A∣的转置行列式记为∣AT∣|A^T|∣AT∣。
- 余子式和代数余子式:将行列式的第iii行和第jjj列去掉,那么剩下的行列式就是aija_{ij}aij的余子式,记为MijM_{ij}Mij,并记Aij=(−1)i+jMijA_{ij}=(-1)^{i+j}M_{ij}Aij=(−1)i+jMij为aija_{ij}aij的代数余子式。
行列式的性质
- 经转置行列式的值不变,即∣AT∣=∣A∣|A^T|=|A|∣AT∣=∣A∣
- 某行有公因式kkk,可把公因式kkk提到行列式外。
∣…………kai1kai2…kain…………∣=k∣…………ai1ai2…ain…………∣\begin{vmatrix} \dots&\dots&\dots&\dots\\ ka_{i1}&ka_{i2}&\dots&ka_{in}&\\ \dots&\dots&\dots&\dots \end{vmatrix} = k\begin{vmatrix} \dots&\dots&\dots&\dots\\ a_{i1}&a_{i2}&\dots&a_{in}&\\ \dots&\dots&\dots&\dots \end{vmatrix} …kai1……kai2……………kain…=k…ai1……ai2……………ain…
特别的:某行元素全为零,则行列式为000。 - 对换行列式某两行的位置,行列式变号。特别的:
- 两行相等,行列式为000,即∣A∣=−∣A∣,∣A∣=0|A|=-|A|,|A|=0∣A∣=−∣A∣,∣A∣=0
- 两行成比例,行列式为000,即k∣A∣=−k∣A∣,∣A∣=0k|A|=-k|A|,|A|=0k∣A∣=−k∣A∣,∣A∣=0
- 某行所有元素都是两个数的和,则可写成两个行列式之和。∣a1+b1a2+b2a3+b3c1c2c3d1d2d3∣=∣a1a2a3c1c2c3d1d2d3∣+∣b1b2b3c1c2c3d1d2d3∣\begin{vmatrix}a_1+b_1&a_2+b_2&a_3+b_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}=\begin{vmatrix}a_1&a_2&a_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}+\begin{vmatrix}b_1&b_2&b_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}a1+b1c1d1a2+b2c2d2a3+b3c3d3=a1c1d1a2c2d2a3c3d3+b1c1d1b2c2d2b3c3d3
- 行列式某行的kkk倍加至另一行,行列式不变。
∣a1+kb1a2+kb2a3+kb3b1b2b3c1c2c3∣=∣a1a2a3b1b2b3c1c2c3∣+k∣b1b2b3b1b2b3c1c2c3∣=∣a1a2a3b1b2b3c1c2c3∣\begin{vmatrix} a_1+kb_1&a_2+kb_2&a_3+kb_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{vmatrix} = \begin{vmatrix} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{vmatrix} {+}k \begin{vmatrix} b_1&b_2&b_3\\b_1&b_2&b_3\\c_1&c_2&c_3 \end{vmatrix} = \begin{vmatrix} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{vmatrix} a1+kb1b1c1a2+kb2b2c2a3+kb3b3c3=a1b1c1a2b2c2a3b3c3+kb1b1c1b2b2c2b3b3c3=a1b1c1a2b2c2a3b3c3 - 按行按列展开式:
- 按iii行展开:∣A∣=ai1Ai1+ai2Ai2+…+ainAin=∑j=1naijAij|A|=a_{i1}A_{i1}+a_{i2}A_{i2}+\ldots+a_{in}A_{in}=\sum_{j=1}^na_{ij}A_{ij}∣A∣=ai1Ai1+ai2Ai2+…+ainAin=j=1∑naijAij
- 按jjj列展开:∣A∣=a1jA1j+a2jA2j+…+anjAnj=∑i=1naijAij|A|=a_{1j}A_{1j}+a_{2j}A_{2j}+\ldots+a_{nj}A_{nj}=\sum_{i=1}^na_{ij}A_{ij}∣A∣=a1jA1j+a2jA2j+…+anjAnj=i=1∑naijAij
- 某一行(列)的所有元素与另一行(列)相应元素的代数余子式乘积之和等于000:
a11A31+a12A32+a13A33=0a_{11}A_{31}+a_{12}A_{32}+a_{13}A_{33}=0\\ a11A31+a12A32+a13A33=0
证明:已知
∣A∣=∣a11a12a13a21a22a23a31a32a33∣|A|= \begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{vmatrix} ∣A∣=a11a21a31a12a22a32a13a23a33
构造以下行列式:
∣B∣=∣a11a12a13a21a22a23a11a12a13∣=0=a11A31+a12A32+a13A33|B|= \begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{11}&a_{12}&a_{13} \end{vmatrix} =0 =a_{11}A_{31}+a_{12}A_{32}+a_{13}A_{33} ∣B∣=a11a21a11a12a22a12a13a23a13=0=a11A31+a12A32+a13A33
因为∣B∣|B|∣B∣的A31A_{31}A31,A32A_{32}A32,A33A_{33}A33和∣A∣|A|∣A∣的相等,所以:
a11A31+a12A32+a13A33=0a_{11}A_{31}+a_{12}A_{32}+a_{13}A_{33}=0\\ a11A31+a12A32+a13A33=0
重要公式
- 上(下)三角行列式的值:∣a11a12…a1n0a22…a2n⋮⋮⋮00…ann∣=∣a110…0a21a22…0⋮⋮⋮an1an2…ann∣=a11a22…ann\begin{vmatrix}a_{11}&a_{12}&\ldots& a_{1n}\\0&a_{22}&\ldots&a_{2n}\\\vdots&\vdots&&\vdots\\0&0&\ldots&a_{nn}\end{vmatrix}=\begin{vmatrix}a_{11}&0&\ldots& 0\\a_{21}&a_{22}&\ldots&0\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\ldots&a_{nn}\end{vmatrix}=a_{11}a_{22}\dots a_{nn}a110⋮0a12a22⋮0………a1na2n⋮ann=a11a21⋮an10a22⋮an2………00⋮ann=a11a22…ann
- 副对角线行列式的值:∣a11a12…a1na21a22…0⋮⋮⋮an10…0∣=∣0…0a1n0…a2(n−1)a2n⋮⋮⋮an1…an(n−1)ann∣=(−1)n(n−1)2a1na2(n−1)…an1\begin{vmatrix}a_{11}&a_{12}&\ldots& a_{1n}\\a_{21}&a_{22}&\ldots&0\\\vdots&\vdots&&\vdots\\a_{n1}&0&\ldots&0\end{vmatrix}=\begin{vmatrix}0&\dots&0& a_{1n}\\0&\dots&a_{2(n-1)}&a_{2n}\\\vdots&&\vdots&\vdots\\a_{n1}&\dots&a_{n(n-1)}&a_{nn}\end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2(n-1)}\dots a_{n1}a11a21⋮an1a12a22⋮0………a1n0⋮0=00⋮an1………0a2(n−1)⋮an(n−1)a1na2n⋮ann=(−1)2n(n−1)a1na2(n−1)…an1
- 范德蒙行列式:
∣11…1a1a2…ana12a22…an2⋮⋮⋮a1n−1a2n−1…ann−1∣=∏1≤j<i≤n(ai−aj)\begin{vmatrix} 1&1&\dots&1\\ a_1&a_2&\dots&a_n\\ a_1^2&a_2^2&\dots&a_n^2\\ \vdots&\vdots&&\vdots\\ a_1^{n-1}&a_2^{n-1}&\dots&a_n^{n-1} \end{vmatrix} = \prod_{1≤j<i≤n}(a_i-a_j) 1a1a12⋮a1n−11a2a22⋮a2n−1…………1anan2⋮ann−1=1≤j<i≤n∏(ai−aj)
证明:假设n−1n-1n−1时,∣An−1∣=∏1≤j<i≤n−1(ai−aj)|A_{n-1}|=\prod_{1≤j<i≤n-1}(a_i-a_j)∣An−1∣=∏1≤j<i≤n−1(ai−aj)成立,对于nnn阶行列式∣An∣|A_n|∣An∣,将上一行的的−a1-a_1−a1倍加到下一行,由n−1n-1n−1行开始,得
∣11…10a2−a1…an−a10a22−a1a2…an2−a1an⋮⋮⋮0a2n−1−a1a2n−2…ann−1−anann−2∣=∣a2−a1a3−a1…an−a1a2(a2−a1)a3(a3−a1)…an(an−a1)⋮⋮⋮a2n−1(a2−a1)a3n−1(a3−a1)…ann−1(an−a1)∣=(a2−a1)(a3−a1)…(an−a1)∣11…1a1a2…ana12a22…an2⋮⋮⋮a1n−2a2n−2…ann−2∣=(a2−a1)(a3−a1)…(an−a1)∏1≤j<i≤n−1(ai−aj)=∏1≤j<i≤n(ai−aj)\begin{vmatrix} 1&1&\dots&1\\ 0&a_2-a_1&\dots&a_n-a_1\\ 0&a_2^2-a_1a_2&\dots&a_n^2-a_1a_n\\ \vdots&\vdots&&\vdots\\ 0&a_2^{n-1}-a_1a_2^{n-2}&\dots&a_n^{n-1}-a_na_n^{n-2} \end{vmatrix}\\\ \\= \begin{vmatrix} a_2-a_1&a_3-a_1&\dots&a_n-a_1\\ a_2(a_2-a_1)&a_3(a_3-a_1)&\dots&a_n(a_n-a_1)\\ \vdots&\vdots&&\vdots\\ a_2^{n-1}(a_2-a_1)&a_3^{n-1}(a_3-a_1)&\dots&a_n^{n-1}(a_n-a_1) \end{vmatrix}\\\ \\= (a_2-a_1)(a_3-a_1)\dots(a_n-a_1) \begin{vmatrix} 1&1&\dots&1\\ a_1&a_2&\dots&a_n\\ a_1^2&a_2^2&\dots&a_n^2\\ \vdots&\vdots&&\vdots\\ a_1^{n-2}&a_2^{n-2}&\dots&a_n^{n-2} \end{vmatrix}\\\ \\=(a_2-a_1)(a_3-a_1)\dots(a_n-a_1)\prod_{1≤j<i≤n-1}(a_i-a_j)\\\ \\=\prod_{1≤j<i≤n}(a_i-a_j) 100⋮01a2−a1a22−a1a2⋮a2n−1−a1a2n−2…………1an−a1an2−a1an⋮ann−1−anann−2 =a2−a1a2(a2−a1)⋮a2n−1(a2−a1)a3−a1a3(a3−a1)⋮a3n−1(a3−a1)………an−a1an(an−a1)⋮ann−1(an−a1) =(a2−a1)(a3−a1)…(an−a1)1a1a12⋮a1n−21a2a22⋮a2n−2…………1anan2⋮ann−2 =(a2−a1)(a3−a1)…(an−a1)1≤j<i≤n−1∏(ai−aj) =1≤j<i≤n∏(ai−aj) - 拉普拉斯展开式:
∣Am∗OBn∣=∣AmO∗Bn∣=∣Am∣∗∣Bn∣\begin{vmatrix}A_m&*\\O&B_n\end{vmatrix}=\begin{vmatrix}A_m&O\\*&B_n\end{vmatrix}=|A_m|*|B_n|AmO∗Bn=Am∗OBn=∣Am∣∗∣Bn∣ ∣OAmBn∗∣=∣∗AmBnO∣=(−1)nm∣Am∣∗∣Bn∣\begin{vmatrix}O&A_m\\B_n&*\end{vmatrix}=\begin{vmatrix}*&A_m\\B_n&O\end{vmatrix}=(-1)^{nm}|A_m|*|B_n|OBnAm∗=∗BnAmO=(−1)nm∣Am∣∗∣Bn∣ - 特征多项式:设A=(aij)A=(a_{ij})A=(aij)是333阶矩阵,则AAA的特征多项式∣λE−A∣=λ3−(a11+a22+a33)λ2+s2λ−∣A∣\begin{vmatrix}\lambda E-A \end{vmatrix}=\lambda^{3}-(a_{11}+a_{22}+a_{33})\lambda^2+s_2\lambda-|A|λE−A=λ3−(a11+a22+a33)λ2+s2λ−∣A∣其中s2=∣a11a12a21a22∣+∣a11a13a31a33∣+∣a11a22a32a33∣s_2=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}+\begin{vmatrix}a_{11}&a_{13}\\a_{31}&a_{33}\end{vmatrix}+\begin{vmatrix}a_{11}&a_{22}\\a_{32}&a_{33}\end{vmatrix}s2=a11a21a12a22+a11a31a13a33+a11a32a22a33
克拉默法则
若nnn个未知数、nnn个方程的线性方程组:{a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2…an1x1+an2x2+⋯+annxn=bn\begin{cases}a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\\dots\\a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\\end{cases}⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2…an1x1+an2x2+⋯+annxn=bn的系数行列式:D=∣A∣=∣a11a12…a1na21a22…a2n⋮⋮⋮an1an2…ann∣≠0D=|A|=\begin{vmatrix}a_{11}&a_{12}&\dots&a_{1n}\\a_{21}&a_{22}&\dots&a_{2n}\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\dots&a_{nn}\end{vmatrix}≠0D=∣A∣=a11a21⋮an1a12a22⋮an2………a1na2n⋮ann=0则方程组有唯一解:x1=D1D,x2=D2D,…,xn=DnDx_1=\frac{D_1}{D},x_2=\frac{D_2}{D},\dots,x_n=\frac{D_n}{D}x1=DD1,x2=DD2,…,xn=DDn其中Dj=∑i=1nbiAij=∣a11…a1,j−1b1a1,j+1…a1na21…a2,j−1b2a2,j+1…a2n⋮⋮⋮⋮⋮an1…an,j−1b1an,j+1…ann∣(j=1,2,…,n)D_j=\sum_{i=1}^nb_iA_{ij}=\begin{vmatrix}a_{11}&\dots&a_{1,j-1}&b_1&a_{1,j+1}&\dots&a_{1n}\\a_{21}&\dots&a_{2,j-1}&b_2&a_{2,j+1}&\dots&a_{2n}\\\vdots&&\vdots&\vdots&\vdots&&\vdots\\a_{n1}&\dots&a_{n,j-1}&b_1&a_{n,j+1}&\dots&a_{nn}\end{vmatrix}(j=1,2,\dots,n)Dj=i=1∑nbiAij=a11a21⋮an1………a1,j−1a2,j−1⋮an,j−1b1b2⋮b1a1,j+1a2,j+1⋮an,j+1………a1na2n⋮ann(j=1,2,…,n)
若齐次方程组:{a11x1+a12x2+⋯+a1nxn=0a21x1+a22x2+⋯+a2nxn=0…an1x1+an2x2+⋯+annxn=0\begin{cases}a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=0\\a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=0\\\dots\\a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=0\\\end{cases}⎩⎨⎧a11x1+a12x2+⋯+a1nxn=0a21x1+a22x2+⋯+a2nxn=0…an1x1+an2x2+⋯+annxn=0的系数行列式D≠0D\neq0D=0,则方程组只有零解。若有非零解,则系数行列式D=0D=0D=0。
补充知识
- ∑i=1nkai=k∑i=1nai\sum_{i=1}^nka_i=k\sum_{i=1}^na_i i=1∑nkai=ki=1∑nai
- ∑i=1n(ai+bi)=∑i=1nai+∑i=1nbi\sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i i=1∑n(ai+bi)=i=1∑nai+i=1∑nbi
- ∑i=1m∑j=1naij=∑j=1n∑i=1maij\sum_{i=1}^m\sum_{j=1}^na_{ij}=\sum_{j=1}^n\sum_{i=1}^ma_{ij} i=1∑mj=1∑naij=j=1∑ni=1∑maij
相关文章:

线性代数——行列式
文章目录版权声明排列行列式行列式的由来行列式的概念行列式的性质重要公式克拉默法则补充知识版权声明 本文大部分内容皆来自李永乐老师考研教材和视频课。 排列 由1,2,…,n1,2,\ldots,n1,2,…,n组成的有序数组称为一个nnn阶排列,通常使用j1j2…jnj_1j_2\ldots …...

Spring注解-Spring-boot-SpingAOP
Spring各个模块 Test 对应spring-test.jar. Spring提供的测试工具, 可以整合JUnit测试, 简化测试环节. Core Container Spring的核心组件, 包含了Spring框架最基本的支撑. Beans, 对应spring-beans.jar. Spring进行对象管理时依赖的jar包. Core, 对应spring-core.jar,…...

使用Shell传参解决DataPhin中PySpark不支持中文的问题
使用Shell传参解决DataPhin中PySpark不支持中文的问题 背景 笔者开发PySpark任务时【别问为神马不用Java和Scala打Jar包的方式,PySpark不需要打包所以开发效率极高,早点搞完早点下班】,遇到一个令所有SQL Boy都很头疼的问题,那就…...
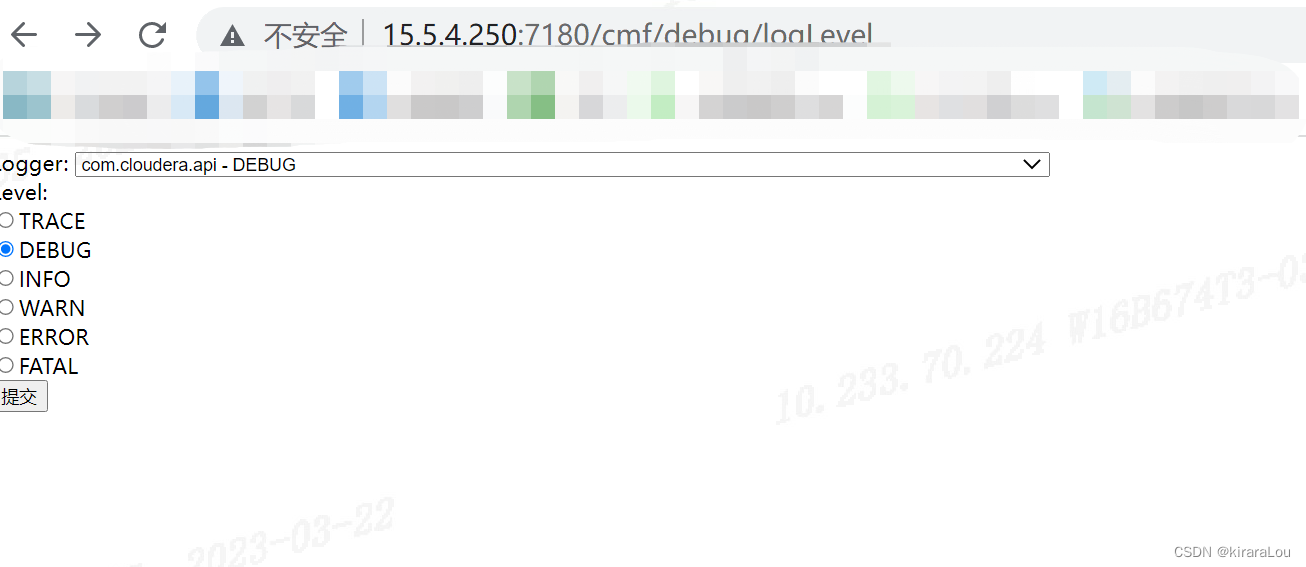
【CDH】cloudera manger 如何开启Debug 日志调试模式
前言 在安装 Cloudera Manger 时,遇到报错,需要开启Debug 日志级别来排查下问题原因。这里记录下 CM 如何开启 Debug 级别。 方法一:为整个服务启动DEBUG 如果 CM 无法启动,则可以为整个服务器启用 DEBUG 或 TRACE。 警告&…...

SQL Server 用户授权与回收
创建xxbbbb账号,账号可以在Company_report20221019.dbo.qfacccmprf表中进行select、 insert,update,delete --创建登录账号 create login xxbbbb with password12345#---创建用户 use Company_report20221019 create user xxbbbb for login xxbbbb---将qfacccmprf表…...

电脑出现乱码的原因以及解决方法
在日常使用电脑的过程中,经常会遇到电脑出现乱码,那么为什么会出现乱码呢?出现乱码又该怎么解决呢?下面我们一起来了解一下。 出现乱码的原因 系统乱码:主要是Windows中显示乱码,比如菜单、桌面、启动界面…...

网络工程师笔记
第一天: 编码就是转化为数字信号;调制就是转化为模拟信号; 调制: 1、基带调制(不改变频率,只改变波形) 2、带通调制(迁移到较高的频段进行传输) (1&…...

linux用户添加用户组与目录切换用户组的操作记录
linux用户添加到多个组 usermod -G groupname username (这种会把用户从其他组中去掉,只属于该组) 如:usermod -G git git (git只属于git组) usermod -a -G groupname username (把用户添加到这个组,之前所属组不影响) 如:usermod…...

在CentOS 7上使用二进制文件安装单节点Kubernetes的详细步骤:
确保您的系统已经安装了Docker和etcd。如果没有,请按照以下命令安装它们: yum install docker etcd 启动Docker服务并将其设置为开机自启: systemctl start docker systemctl enable docker 下载所需的Kubernetes二进制文件。您可以从以下网…...
iCollections for mac 8.0.6.80608 保持Mac桌面的整洁
应用介绍 iCollections允许您在桌面上创建区域,以便您可以排序和排列图标。这可以帮助您将相关项目保持在一起,以便文件(图片,文档,屏幕截图,应用程序等)井井有条且易于查找。 小麦测试可以按照…...
学习HM微博项目第8天
步骤:发微博01-导航栏内容 -> 发微博02-自定义TextView -> 发微博03-完善TextView和发送微博按钮 -> 发微博04-显示工具条 -> 发微博05-封装工具条和相册 -> 发微博06-发送微博 发微博01-导航栏内容 APP的演示操作: 从APP的演示操作中可…...
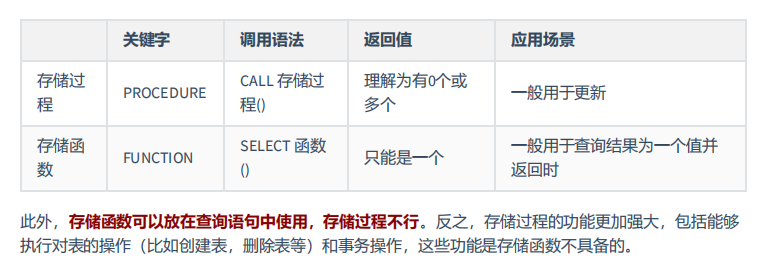
十五、存储过程与函数
一、存储过程概述 1、简介 含义:存储过程的英文是 Stored Procedure 。它的思想很简单,就是一组经过 预先编译 的 SQL 语句的封装 执行过程:存储过程预先存储在 MySQL 服务器上,需要执行的时候,客户端只需要向服务器…...
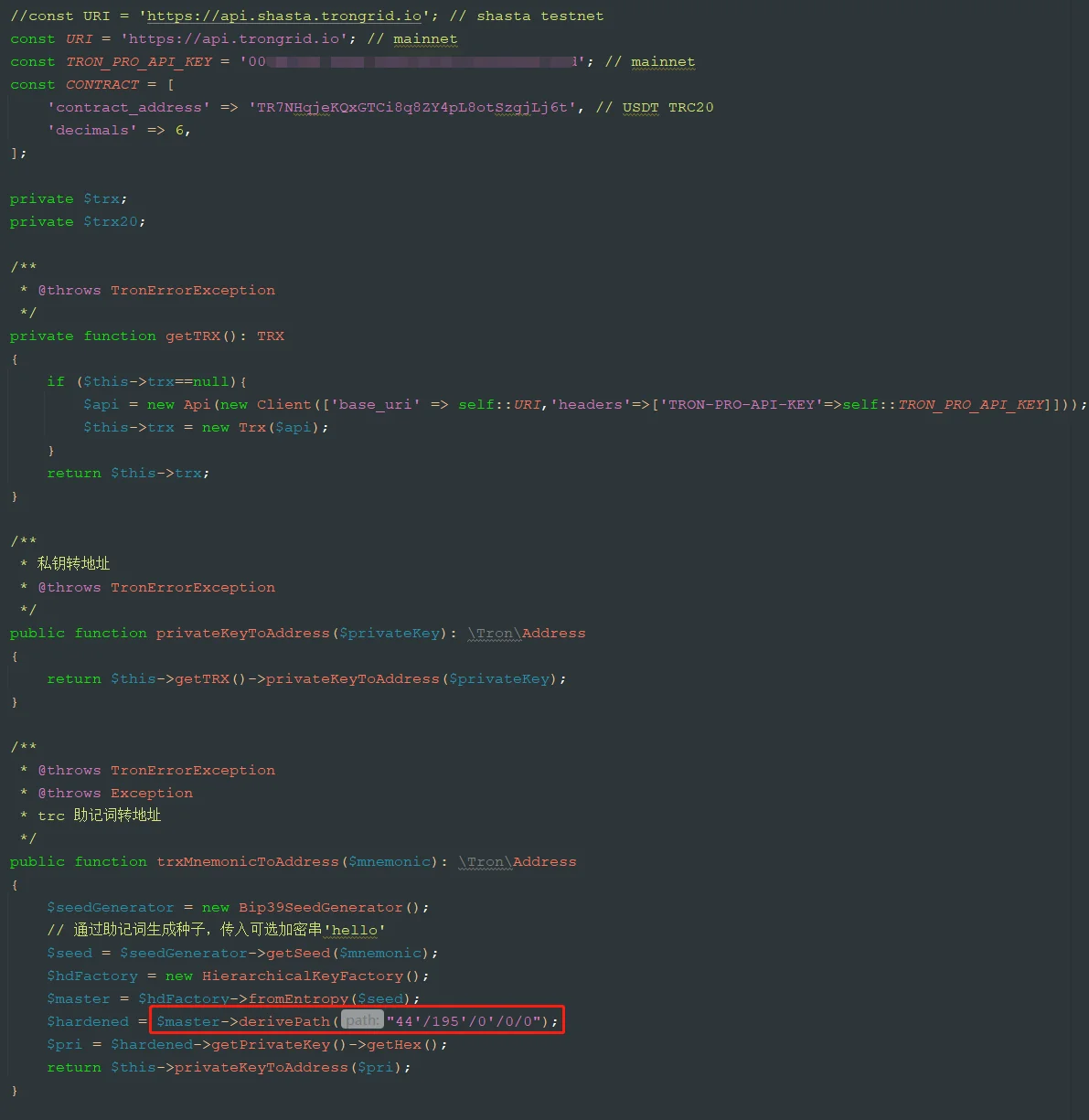
php实现助记词转TRX,ETH 私钥和钱包地址
TRX助记词转地址网上都是Java,js或其他语言开发的示例,一个简单的功能需要依赖其他环境来实现表示不能忍,毕竟php是世界上最好的语言。【狗头】 一、知识准备 要实现助记词转TRX私钥和地址,先需要知道助记词和私钥钱包地址之间的…...

浅析可观测系统中sdk的不同引入方式的利与弊
文章前提是不考虑sw的方式引入,同时不考虑在nginx等自动注入js脚本的方式,那么基本就是两种大的形式:cdn引入和本地引入其中cdn引入有两种:cdn同步cdn异步本地引入有两种:npm本地js文件参考知识提前先补充一张图片正文…...
)
Google Earth导入经纬高(txt文件)
目录 一、提取GNSS数据生成txt文本文件 二、Google Earth导入txt文件 1、启动Google Earth 2、打开vig_result.txt...

Unity客户端开发工程师的进阶之路
UWA技能成长系统是UWA根据学员的职业发展目标,提供技能学习的推荐路径,再将所需学习内容按难易等多维度,设计分成多个学习阶段,可以循序渐进地进行学习。 进入技能成长体系,目标选择高级客户端开发工程师(U…...

2023年全国最新高校辅导员精选真题及答案34
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 72.心理发展的特点是()。 A.方向性与不可逆性 B.连续性与阶段性…...

chatGPT身份指令
充当 Linux 终端 我想让你充当 Linux 终端。我将输入命令,您将回复终端应显示的内容。我希望您只在一个唯一的代码块内回复终端输出,而不是其他任何内容。不要写解释。除非我指示您这样做,否则不要键入命令。当我需要用英语告诉你一些事情时&…...

基于springboot实现私人健身与教练预约管理系统【源码+论文】分享
基于springboot实现私人健身与教练预约管理系统演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea M…...

网络技术领域术语大全,含中英文及缩写,强烈建议收藏!
你好,这里是网络技术联盟站。 今天给大家分享的是网络技术领域相关的术语大全,在文末,我已经将本文整理成一个pdf文档了,大家可以下载到本地以便查阅。 自主访问控(DAC:Discretionary Access Control) 自主访问控制(DAC)是一个…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
