Codeforces Round 973 (Div. 2) - D题
传送门:Problem - D - Codeforces
题目大意:

思路:
尽量要 最大值变小,最小值变大
即求 最大值的最小 和 最小值的最大 -> 二分答案
AC代码:
代码有注释
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{int n; cin >> n;vector<int> a(n + 1), b(n + 1);for (int i = 1; i <= n; i++) cin >> a[i];auto check1 = [&](int limit){// limit 此时就是 最大值的最小值// 经过操作后,若 b[i] <= limit 就是ok的,否则就放弃这个值// 最大值最小for (int i = 1; i <= n; i++) b[i] = a[i];for (int i = 1; i < n; i++){// b[i] 超过 limit ,就要减小 b[i]if (b[i] > limit){b[i + 1] += (b[i] - limit);b[i] = limit;}}for (int i = 1; i <= n; i++){if (b[i] > limit) return false;}return true;};int left = 0; int right = 1e12;while (right > left){int mid = left + right >> 1;if (check1(mid))right = mid;else left = mid + 1;}int ans = left;auto check2 = [&](int limit){// 最小值最大// limit 就是最小值的最大值for (int i = 1; i <= n; i++) b[i] = a[i];for (int i = 1; i < n; i++){if (b[i] > limit){b[i + 1] += (b[i] - limit);b[i] = limit;}}int mn = 2e18;for (int i = 1; i <= n; i++) mn = min(mn, b[i]);// 经过操作后,mn 仍大于 limit ,则可以继续增大limitif (mn >= limit)return true;else return false;};left = 0; right = 1e12;while (right > left){int mid = left + right + 1 >> 1;if (check2(mid))left = mid;else right = mid - 1;}cout << ans - left << endl;
}
signed main()
{int tt; cin >> tt;while (tt--)solve();return 0;
}
加练二分:
传送门:Problem - D - Codeforces
题目大意:


思路:
二分 顶点1要加上的值
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
const int N = 2e5 + 10;
int h[N], e[N], ne[N], idx;
int a[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool dfs(int u, int limit)
{if( limit > 1e9 ) return false; // 一定要加这个代码,否则就会爆 long long// 所有顶点的值都是 <= 1e9 的,所以 limit 肯定不能大于 1e9if (a[u] < limit){int temp = limit - a[u];limit += temp;}bool flag = false;for (int i = h[u]; i != -1; i = ne[i]){flag = true;int j = e[i];if (!dfs(j, limit)) return false;}if (!flag){if (a[u] >= limit) return true;else return false;}else return true;
}
bool check(int limit)
{for (int i = h[1]; i != -1; i = ne[i]){int j = e[i];if (!dfs(j, limit)) return false;}return true;
}
void solve()
{memset(h, -1, sizeof h); idx = 0;cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 2; i <= n; i++){int fa; cin >> fa;add(fa, i);}int left = 0; int right = 1e9;while (right > left){int mid = left + right + 1 >> 1;if (check(mid)) left = mid;else right = mid - 1;}cout << a[1] + left << endl;
}
signed main()
{int tt; cin>> tt;while(tt--)solve();return 0;
}相关文章:

Codeforces Round 973 (Div. 2) - D题
传送门:Problem - D - Codeforces 题目大意: 思路: 尽量要 最大值变小,最小值变大 即求 最大值的最小 和 最小值的最大 -> 二分答案 AC代码: 代码有注释 #include<bits/stdc.h> using namespace std; #…...

threejs性能优化之gltf文件压缩threejs性能优化之glb文件压缩
在使用Three.js进行3D图形开发时,GLTF(GL Transmission Format)文件因其高效性和灵活性而广受欢迎。然而,随着模型复杂度的增加,GLTF文件的大小也会显著增加,这可能会对加载时间和渲染性能产生负面影响。为…...

设计模式 享元模式(Flyweight Pattern)
享元模式 简绍 享元模式(Flyweight Pattern)是一种结构型设计模式,它的目的是通过共享技术来有效地支持大量细粒度的对象。享元模式可以极大地减少内存的使用,从而提高程序的性能。它特别适用于需要创建大量相似对象的场景&#…...

Leetcode 3290. Maximum Multiplication Score
Leetcode 3290. Maximum Multiplication Score 1. 解题思路2. 代码实现 题目链接:3290. Maximum Multiplication Score 1. 解题思路 这一题的话就是一个比较暴力的动态规划,这里就不过多展开了,参考代码看一下就行。 2. 代码实现 给出py…...

CefSharp_Vue交互(Element UI)_WinFormWeb应用(3)---通过页面锁屏和关机(含示例代码)
一、预览 实现功能:通过vue标题栏按钮锁屏和关机 1.1 预览 1.2 代码 锁屏代码csharp LockWorkStation() 关机代码chsharp 注意vue代码参数和此参数一致(0/1/2) 方法ExitWindowsEx()...

unity UnityWebRequest 的request.downloadHandler 空应用
unity UnityWebRequest 的request.downloadHandler 空应用 private IEnumerator Test_Get() {UnityWebRequest request new UnityWebRequest(tmp_getURL, "GET");yield return request.SendWebRequest();if (request.result UnityWebRequest.Result.ConnectionErr…...
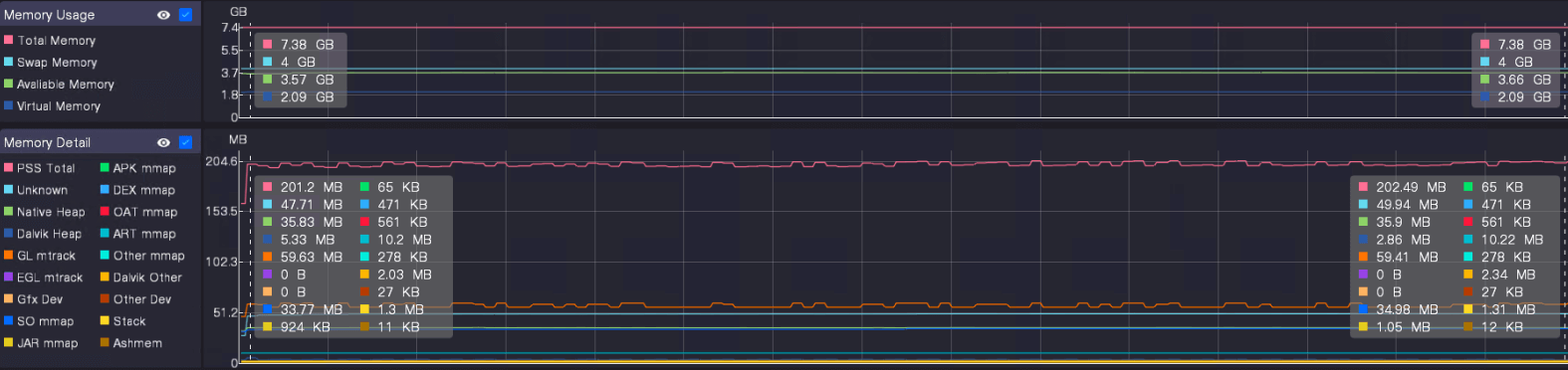
使用 UWA Gears 定位游戏内存问题
UWA Gears 是UWA最新发布的无SDK性能分析工具。针对移动平台,提供了实时监测和截帧分析功能,帮助您精准定位性能热点,提升应用的整体表现。 内存不足、内存泄漏和过度使用等问题,常常导致游戏出现卡顿、崩溃,甚至影响…...

OpenRestry(一个Nginx集成工具)的安装与使用
文章目录 一、OpenRestry介绍1、什么是Nginx呢?2、Nginx的反向代理3、Nginx的作用4、什么是OpenRestry? 二、OpenRestry的安装三、OpenRestry中nginx的使用1、Ngnix可以当做web服务器2、Nginx中可以编写Lua脚本 一、OpenRestry介绍 要想了解什么是OpenR…...

linux操作系统的基本命令
1.linux下的文件系统 在linux操作目录下没有像window操作系统下盘符的概念,只有一个根目录/,所有文件目录都在它的下面 linux的目录结构: 在Linux系统中: 文件都从跟目录开始的,用/表示文件名称区分大小写路径都是以/俩进行分隔(windown用\分隔)以.开头的文件为隐藏文件 Li…...

通过UV快速计算品牌独立站网络流量
背景: 品牌独立站项目交付过程中,我们需要为客户提供“云资源” 成本报价,其中“计算资源” 及CPU、内存、存储 参数相对固定,而互联网网络成本需要进行评估报价,以海外TOP云平台 AWS、AZURE、GCP 为例都是以“不限带…...

使用Kong开源API网关的保姆级教程
什么是Kong? Kong是一个开源的、云原生、高性能的API网关,可以轻松地为任何服务提供管理、保护和扩展。它提供了一个可扩展的插件生态系统,可以满足各种各样的需求,如身份验证、授权、限流、监控等。 安装Kong 1. 环境准备 操作系统: CentOS、Ubuntu等主流Linux发行版D…...

浅谈Spring Cloud:认识微服务
SpringCloud就是分布式微服务架构的一站式解决方案,是微服务架构落地的多种技术的集合。 目录 微服务远程调用 Eureka注册中心 搭建Eureka Server 注册组件 服务拉取 当各种各样的服务越来越多,拆分的也越来越细,此时就会出现一个服务集…...

mac命令行分卷压缩与合并
对当前目录内的文件压缩的同时分卷 //语法:zip -r -s 1m 压缩文件名.zip 当前路径 zip -r -s 1m split.zip . //解压 zip -s 0 split.zip --out unsplit.zip unzip unsplit.zip 将一个zip文件进行分卷 一个900k的压缩包名为hello.zip,将其分割为每500K一个zip zip - hello.…...
 编译 OpenJDK 8)
在 Linux (aarch64) 编译 OpenJDK 8
环境信息 操作系统:Rocky Linux 9.4 (aarch64)Open JDK:OpenJDK 8u422Boot JDK:jdk8u421-linux-aarch64 编译 OpenJDK 需要有一个 JDK。 解压后当前目录结构如下: /opt/ ├── jdk1.8.0_421 │ ├── COPYRIGHT │ ├──…...

如何有效检测住宅IP真伪?
在当今的互联网时代,住宅IP(即家庭用户通过宽带服务提供商获得的IP地址)在跨境电商、广告投放、网络安全等多个领域扮演着重要角色。然而,随着网络环境的复杂化和欺诈行为的增多,如何有效检测和辨别住宅IP的真伪成为了…...

springboot acuturator
SpringBoot使用Actuator - 基础使用步骤 Spring Boot 监控端点 Actuator 入门 - 系统学习 Spring Boot Admin入门 - 基础学习 Spring Boot 监控工具 Admin 入门 - 进阶学习 Spring Boot 监控平台 Prometheus Grafana 入门 Spring Boot 链路追踪 SkyWalking 入门...

什么是SaaS软件?有哪些常用的SaaS软件?
SaaS(Software as a Service,软件即服务)是一种通过互联网提供软件的模式,用户无需安装和维护任何复杂的基础设施,只需通过网络连接即可使用软件。SaaS 供应商负责软件的维护、升级和可用性,用户则通过订阅…...

QT Layout布局,隐藏其中的某些部件后,不影响原来的布局
最近在工作时,被要求,需要将布局中的某些部件隐藏后,但不能影响原来的布局。 现在记录解决方案! 一、水平布局(垂直布局一样) ui中的布局 效果: 按钮可以任意隐藏,都不影响其中布…...
WPF自定义Dialog模板,内容用不同的Page填充
因为审美的不同,就总有些奇奇怪怪的需求,使用框架自带的对话框已经无法满足了,这里记录一下我这边初步设计的对话框。别问为啥要用模板嵌套Page来做对话框,问就是不想写太多的窗体。。。。 模板窗体(XAML)…...

[数据集][目标检测]智慧养殖场肉鸡健康状态检测数据集VOC+YOLO格式4657张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):4657 标注数量(xml文件个数):4657 标注数量(txt文件个数):4657 标注…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
