【力扣】2376. 统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
示例 1:
输入:n = 20
输出:19
解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。
示例 2:
输入:n = 5
输出:5
解释:1 到 5 所有整数都是特殊整数。
示例 3:
输入:n = 135
输出:110
解释:从 1 到 135 总共有 110 个整数是特殊整数。
不特殊的部分数字为:22 ,114 和 131 。
public class SpecialNumberCounter { public static int countSpecialNumbers(int n) { if (n < 1) return 0; int count = 0; int length = (int) Math.log10(n) + 1; // 获取 n 的位数 // 从 1 到 length-1 位数的情况 for (int i = 1; i < length; i++) { count += countSpecialNumbersWithFixedLength(i, 9); // 每一位的数字可以是 1-9 中的任意一个 } // 处理长度为 length 的数 int[] usedDigits = new int[10]; // 用于标记哪些数字已被使用 for (int i = 1; i <= n; i *= 10) { int currentDigit = n / i % 10; // 获取当前位的数字 if (currentDigit == 0) { // 如果当前位是 0,则不能包含 0 作为特殊整数的最高位 // 但我们已经在前面的循环中处理了所有不包含 0 作为最高位的情况 // 所以这里直接跳过,不需要做任何处理 continue; } // 从当前位开始,生成所有可能的特殊整数 count += generateSpecialNumbers(n, i, currentDigit, usedDigits); // 如果当前位小于 n 的对应位,那么可以包含从 0 到 currentDigit-1 的所有数字作为下一位的开头 // 但因为我们要的是互不相同的数位,所以实际上不能包含已经使用过的数字 // 但由于我们是从高位到低位遍历,所以这里不需要显式处理 // 标记当前位已经使用 usedDigits[currentDigit] = 1; // 如果某一位是 0 并且不是最高位,那么后面的位可以自由选择(因为我们已经处理过最高位不为 0 的情况) // 但由于我们是按位遍历的,所以这种情况会在下一轮循环中自动处理 } return count; } // 生成长度为 length,且以 firstDigit 开头的特殊整数数量(不超过 max) private static int generateSpecialNumbers(int max, int base, int firstDigit, int[] usedDigits) { if (max < base) return 0; // 如果 max 已经小于当前位的 base,则无法生成更多的特殊整数 int count = 0; usedDigits[firstDigit] = 1; // 标记 firstDigit 已被使用 // 从 firstDigit+1 开始,选择剩余的数位 for (int i = firstDigit + 1; i < 10; i++) { if (usedDigits[i] == 0) { // 如果 i 没有被使用过 int remaining = max % base / (base / 10); // 剩余需要匹配的数位(不包括当前位) if (remaining >= i) { // 如果剩余数位可以包含 i count += generateSpecialNumbers(max, base / 10, i, usedDigits) + 1; // +1 表示当前这个数本身 } } } usedDigits[firstDigit] = 0; // 恢复 usedDigits 数组 // 加上不以任何数字开头的特殊整数(即只有 firstDigit 的情况) if (max >= base * firstDigit) { count++; } return count; } // 计算固定长度的特殊整数数量(不包含前导零) private static int countSpecialNumbersWithFixedLength(int length, int maxDigit) { int count = 9; // 第一位不能为 0,所以有 9 种选择 for (int i = 1; i < length; i++) { count *= maxDigit - i; // 后续每一位都有 maxDigit - i 种选择(因为已经选择了 i 个数字) } return count; } public static void main(String[] args) { int n = 20; System.out.println(countSpecialNumbers(n)); // 输出: 11 n = 1000; System.out.println(countSpecialNumbers(n)); // 输出一个更大的范围内的特殊整数数量 }
}
注意:上面的代码可能并不是最优解,并且包含了一些简化和假设(比如没有显式处理最高位为 0 的情况,因为题目通常意味着特殊整数是正整数,且没有前导零)。此外,generateSpecialNumbers 方法可能不是最高效的实现,因为它在递归过程中重复计算了一些情况。一个更优化的实现可能会使用动态规划或记忆化搜索来避免重复计算。
然而,这个实现应该能够给出正确的答案,并且对于不是特别大的 n 来说,性能是可以接受的。对于非常大的 n,我们可能需要进一步优化算法或使用更高效的数据结构。
相关文章:

【力扣】2376. 统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。 给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。 示例 1: 输入:n 20 输出:19 解释:1 到 20 之间所有整数除了 11 以外都…...

MySQL面试题——第一篇
1. 一张自增表里面总共有7条数据,删除了最后2条数据,重启数据库后又插入了一条数据,此时ID是几 表类型如果是MyISAM,那么id就是8 如果是InnoDB,那就是6 InnoDB表只会把自增主键的最大id记录在内存中,所以重…...
零停机部署的“秘密武器”:为什么 Kamal Proxy 能成为你架构中的不二之选?
你是不是也遇到过这种场景:网站正在升级,用户却被迫刷新无数次页面?服务器切换时瞬间掉线,客户体验差得没话说。更糟糕的是,流量高峰期来临时,正是业务最重要的时刻,结果因为停机而损失惨重。这个时候你一定会想:难道没有一种方式,能在不打断服务的情况下,平滑地进行…...
轻量级RSS阅读器Fusion
什么是 Fusion ? Fusion 是一款轻量级、自托管的 RSS 聚合器和阅读器。 软件主要特点: 自动分组、书签、搜索、嗅探信息导入/导出 OPML 文件支持 RSS、Atom、JSON 类型的 feed响应式、明/暗模式、PWA轻量级,自托管友好 使用 Golang 和 SQLit…...

Kubernetes从零到精通(11-CNI网络插件)
Kubernetes网络模型 Kubernetes的网络模型(Kubernetes Networking Model)旨在提供跨所有节点、Pod和服务的统一网络连接。它的核心理念是通过统一的网络通信规则,保证集群中的所有组件能够顺畅地相互通信。Kubernetes网络模型主要有以下几个关…...

【手机马达共振导致后主摄马达声音异常】
手机马达共振导致后主摄马达声音异常 问题根因解决方案其他易混淆 问题根因 当手机马达的震动频率和摄像头AF马达的一二阶震动频率处于共振频段的时候,手机马达震动时候有很大概率会干扰到后置摄像头的对焦马达正常工作,可能出现的影响有出现滋滋杂音&a…...

AUTOSAR UDS NRC
UDS NRC NRC 含义如表格所示 NRC代码描述含义0x00Ok没有错误,请求已成功执行0x01~0x0FISOSAEReservedISO 保留,暂时未定义0x10General reject服务请求被拒绝,原因不明确0x11Service not supported请求的服务不被支持0x12Sub-function not supported请求的子功能不被支持0x13…...

[数据结构]无头单向非循环链表的实现与应用
文章目录 一、引言二、线性表的基本概念1、线性表是什么2、链表与顺序表的区别3、无头单向非循环链表 三、无头单向非循环链表的实现1、结构体定义2、初始化3、销毁4、显示5、增删查改 四、分析无头单向非循环链表1、存储方式2、优点3、缺点 五、总结1、练习题2、源代码 一、引…...

认识结构体
目录 一.结构体类型的声明 1.结构的声明 2.定义结构体变量 3.结构体变量初始化 4.结构体的特殊声明 二.结构体对齐(重点难点) 1.结构体对齐规则 2.结构体对齐练习 (一)简单结构体对齐 (二)嵌套结构体对齐 3.为什么存在内存对齐 4.修改默认对齐数 三.结构体传参 1…...
)
Linux驱动.之MT7601,USB-WiFi网卡移植到X210开发板,wpa_supplicant配置工具的使用(一)
一、移植前 1、下载与解压无线网卡MT7601U驱动源码压缩包 DPO_MT7601U_LinuxSTA_3.0.0.4_20130913.tar.bz2 解压后有如下文件 ate common iwpriv_usage.txt Makefile mgmt phy README_STA_usb RT2870STA.dat sta_ate_iwpriv_usage.txt chips include m…...
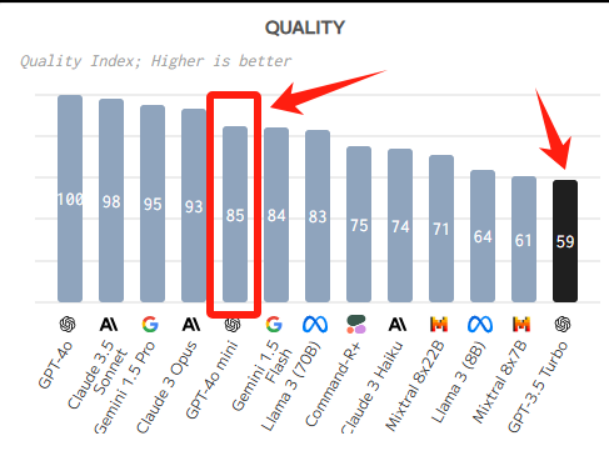
ChatGPT 在国内使用的方法
AI如今很强大,聊聊天、写论文、搞翻译、写代码、写文案、审合同等等,ChatGPT 真是无所不能~ 作为一款出色的大语言模型,ChatGPT 实现了人类般的对话交流,最主要是能根据上下文进行互动。 接下来,我将介绍 ChatGPT 在国…...
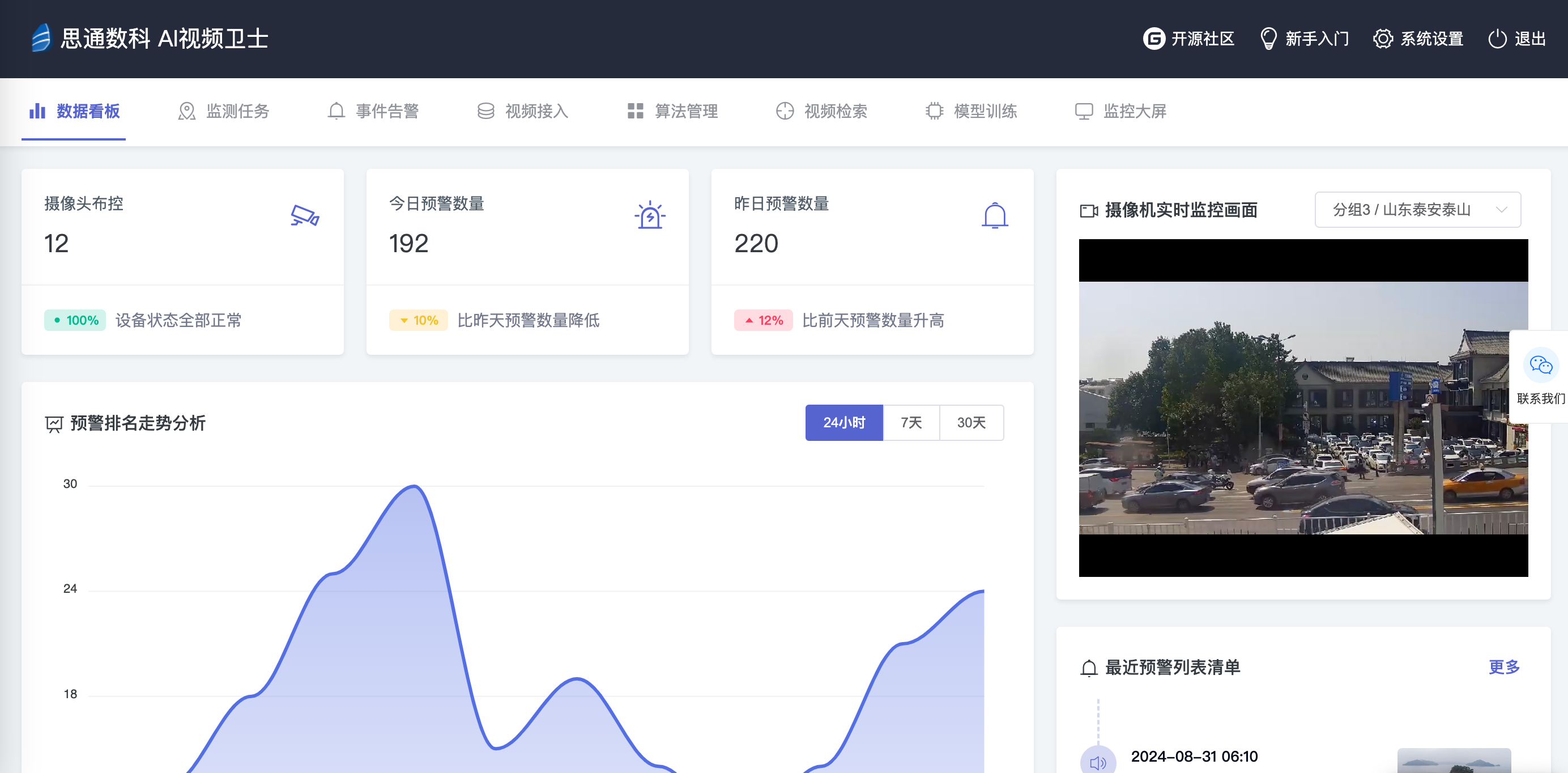
思通数科开源产品:免费的AI视频监控卫士安装指南
准备运行环境: 确保您的服务器或计算机安装了Ubuntu 18.04 LTS操作系统。 按照产品要求,安装以下软件: - Python 3.9 - Java JDK 1.8 - MySQL 5.5 - Redis 2.7 - Elasticsearch 8.14 - FFmpeg 4.1.1 - RabbitMQ 3.13.2 - Minio (…...

阿里HPN-用于大型语言模型训练的数据中心网络
阿里巴巴HPN:用于大型语言模型训练的数据中心网络 探索大规模语言模型训练新方法:阿里巴巴HPN数据中心网络论文。 摘要 本文介绍了阿里云用于大型语言模型(LLM)训练的数据中心网络HPN。由于LLM和一般云计算之间的差异(例如,在流量模式和容错性方面)&…...

re题(27)BUUFCTF-[MRCTF2020]Transform
BUUCTF在线评测 (buuoj.cn) 先到ida,先看一下字符串 找到主函数 int __cdecl main(int argc, const char **argv, const char **envp) {char Str[104]; // [rsp20h] [rbp-70h] BYREFint j; // [rsp88h] [rbp-8h]int i; // [rsp8Ch] [rbp-4h]sub_402230(argc, argv…...

偶数、奇数、整数与指数
引言 在前面的课程中,我们已经学习了 Python 的基本输入输出、数据类型及其转换、顺序结构、分支结构、循环结构、循环控制语句、字符串类型、列表类型、元组类型、字典类型、集合类型、函数的定义与使用、函数调用与作用域、函数的高级应用、质数、倍数与余数。本课…...

关于c#中异步async和await的理解
之前给大家介绍了所谓异步编程的用法,但是没有细致的理解到,今天想和大家一起探讨一下; 前文: C#笔记14 异步编程Async,await,task类-CSDN博客 异步的起初 应用程序会启动一个进程,一个进程可以有很多…...

mysql等保数据库命令
mysql数据库命令 默认安装位置:C:\Program Files\MySQL\MySQL Server 8.0\bin select version() from dual; desc mysql.user; 查看表中有哪些列 1、SELECT user, host, authentication_string, account_locked ,password_lifetime FROM mysql.user; 查询用户表…...

云平台在大规模设备管理和数据分析中的作用
在当代数字化转型的浪潮中,云平台作为信息技术基础设施的核心组件,扮演着无可替代的角色,尤其在大规模设备管理和数据分析领域,其重要性和影响力日益凸显。本文旨在深入探讨云平台如何通过其独特的优势,促进数据的高效…...

数据结构-树和二叉树
树 和 二叉树 1.树的概念 树 tree 是n(n>0)个节点的有限集 在任意的一个非空树中 (1)有且仅有一个特定的被称为 根(root) 的节点 (2)当n>1时, 其余的节点可分为m(m>0)个互不相交的有限集T1, T2, T3, .... …...

树和二叉树的概念以及结构
一起加油学数据结构 目录 树的概念以及结构 树的概念 树的相关概念 树的表示 二叉树的概念以及结构 二叉树的概念 特殊的二叉树 二叉树的性质 二叉树的存储结构 树的概念以及结构 树的概念 树是一种非线性的数据结构,它是由n(n>0)…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
