当前位置： 首页 > news >正文

【算法篇】二叉树类（1）（笔记）

news 2026/2/9 2:17:21

目录

一、认识二叉树

1. 二叉树的种类

（1）满二叉树

（2）完全二叉树

（3）二叉搜索树

（4）平衡二叉搜索树

2. 二叉树的存储方式

3. 二叉树的遍历方式

4. 二叉树的定义

二、Leetcode 题目整理

1. 二叉树的前、中、后序遍历

（1）递归法

（2）迭代法（栈的运用）

（3）标记法（栈的运用）

2. 二叉树的层序遍历

（1）递归法

（2）迭代法

3. 翻转二叉树

（1）广度优先算法

（2）深度优先算法（前、中、后）

（3）递归法

4. 对称二叉树

（1）递归法

（2）迭代法

5. 二叉树的最大深度

6. 二叉树的最小深度

7. 平衡二叉树

8. 二叉树的所有路径

（1）回溯法

（2）迭代法

一、认识二叉树

1. 二叉树的种类

（1）满二叉树

        深度为 k，有 2^k-1 个节点的二叉树。

（2）完全二叉树

        在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。 

（3）二叉搜索树

二叉搜索树是一个有序树。

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树

（4）平衡二叉搜索树

        C++ 中 map、set、multimap，multiset 的底层实现都是 平衡二叉搜索树，所以map、set 的增删操作 时间时间复杂度 是 logn。

2. 二叉树的存储方式

        二叉树可以链式存储，也可以顺序存储。

        链式存储方式就用 指针， 顺序存储的方式就是用 数组。

        在数组存储中：如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

3. 二叉树的遍历方式

二叉树主要有两种遍历方式：

  1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
  2. 广度优先遍历：一层一层的去遍历。

从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：

  • 深度优先遍历
    • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）
  • 广度优先遍历
    • 层次遍历（迭代法）

4. 二叉树的定义

struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

二、Leetcode 题目整理

1. 二叉树的前、中、后序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/566103571/94. 二叉树的中序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-inorder-traversal/description/145. 二叉树的后序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-postorder-traversal/description/

        给你二叉树的根节点 root ，返回它节点值的 前序 / 中序 / 后序遍历。

（1）递归法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/// 前序遍历
class Solution {
public:void traversal(TreeNode* cur, vector<int>& result) {if (cur == NULL) return;result.push_back(cur->val);traversal(cur->left, result);traversal(cur->right, result);}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};// 中序遍历
class Solution {
public:void traversal(TreeNode* cur, vector<int>& result) {if (cur == NULL) return;traversal(cur->left, result);result.push_back(cur->val);traversal(cur->right, result);}vector<int> inorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};// 后序遍历
class Solution {
public:void traversal(TreeNode* cur, vector<int>& result) {if (cur == NULL) return;traversal(cur->left, result);traversal(cur->right, result);result.push_back(cur->val);}vector<int> postorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};

（2）迭代法（栈的运用）

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/// 前序遍历
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> record;vector<int> result;if (root == NULL) return result;record.push(root);while (!record.empty()) {TreeNode* node = record.top();record.pop();result.push_back(node->val);if (node->right) record.push(node->right);if (node->left) record.push(node->left);}return result;}
};// 中序遍历
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点，访问到最底层st.push(cur);cur = cur->left;} else {cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）st.pop();result.push_back(cur->val);cur = cur->right;}}return result;}
};// 后序遍历（前序输出后翻转就可以）
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};

（3）标记法（栈的运用）

        将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。如何标记呢，就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/// 前序遍历
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> record;if (root != nullptr) record.push(root);while (!record.empty()) {TreeNode* node = record.top();if (node != nullptr) {record.pop();if (node->right) record.push(node->right);if (node->left) record.push(node->left);record.push(node);record.push(nullptr);}else {record.pop();node = record.top();record.pop();result.push_back(node->val);}}return result;}
};// 中序遍历
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {// 标记法vector<int> result;stack<TreeNode*> record;if (root != nullptr) record.push(root);while (!record.empty()) {TreeNode* node = record.top();  // 等于nullptr，说明最先处理的节点已经遍历到。叶子结点已经到底，需要打印中间节点// 不等于nullptr，说明还未遍历到最先处理的节点if (node != nullptr) {record.pop(); // 弹出顶部元素，避免重复if (node->right) record.push(node->right);record.push(node);record.push(nullptr);if (node->left) record.push(node->left);}else {record.pop(); // 弹出nullptrnode = record.top();record.pop();result.push_back(node->val);}}return result;}
};// 后序遍历
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> record;if (root != nullptr) record.push(root);while (!record.empty()) {TreeNode* node = record.top();if (node != nullptr) {// 中 nullptr 右 左record.push(nullptr);if (node->right) record.push(node->right);if (node->left) record.push(node->left);}else {record.pop();node = record.top();record.pop();result.push_back(node->val);}}return result;}
};

2. 二叉树的层序遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-level-order-traversal/description/

        给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

 

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]示例 2：
输入：root = [1]
输出：[[1]]示例 3：
输入：root = []
输出：[]

（1）递归法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void order(TreeNode* cur, vector<vector<int>>& result, int depth){if (cur == nullptr) return;// 二叉树的层级是递增的（从根节点开始，逐层向下），且每个层级只会在第一次遇到时执行这行代码// 因此每个层级只会被添加一次对应的 vector<int>()if (result.size() == depth) result.push_back(vector<int>());result[depth].push_back(cur->val);order(cur->left, result, depth + 1);order(cur->right, result, depth + 1);}vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;int depth = 0;order(root, result, depth);return result;}
};

（2）迭代法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;queue<TreeNode*> que;if (root != nullptr) que.push(root);while (!que.empty()) {// 现在que队列中的元素为当前层的节点个数int size = que.size();vector<int> record;for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();record.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(record);}return result;}
};

3. 翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/invert-binary-tree/description/

        给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]示例 2：
输入：root = [2,1,3]
输出：[2,3,1]示例 3：
输入：root = []
输出：[]

        想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。 

（1）广度优先算法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 层序遍历if (!root || (!root->left && !root->right)) return root;queue<TreeNode*> que;que.push(root);while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();swap(node->left, node->right);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return root;}
};

（2）深度优先算法（前、中、后）

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 后序遍历（循环法）stack<TreeNode*> record;if (root != nullptr) record.push(root);while (!record.empty()) {TreeNode* node = record.top();record.pop();if (node != nullptr) {// 栈顶元素不等于 nullptrrecord.push(node);                          // 中 record.push(nullptr);   // 到遍历中节点的时候停一下，需要先遍历右节点if (node->right) record.push(node->right);  // 右if (node->left) record.push(node->left);    // 左}else {node = record.top();record.pop();swap(node->left, node->right);}}return root;}
};class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 中序遍历（循环法）stack<TreeNode*> record;if (root != nullptr) record.push(root);while (!record.empty()) {TreeNode* node = record.top();record.pop();if (node != nullptr) {// 栈顶元素不等于 nullptrif (node->right) record.push(node->right);  // 右record.push(node);                          // 中 record.push(nullptr);   // 遍历完左节点的时候停一下，现处理中节点if (node->left) record.push(node->left);    // 左}else {node = record.top();record.pop();swap(node->left, node->right);}}return root;}
};class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 前序遍历（循环法）stack<TreeNode*> record;if (root != nullptr) record.push(root);while (!record.empty()) {TreeNode* node = record.top();record.pop();if (node != nullptr) {// 栈顶元素不等于 nullptrif (node->right) record.push(node->right);  // 右if (node->left) record.push(node->left);    // 左record.push(node);                          // 中   record.push(nullptr);}else {node = record.top();record.pop();swap(node->left, node->right);}}return root;}
};

（3）递归法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right);  // 中invertTree(root->left);         // 左invertTree(root->right);        // 右return root;}
};

4. 对称二叉树

101. 对称二叉树 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/symmetric-tree/description/

        给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：
输入：root = [1,2,2,3,4,4,3]
输出：true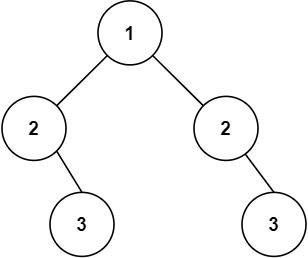

示例 2：
​​​​​​​输入：root = [1,2,2,null,3,null,3]
输出：false

（1）递归法

① 终止条件

  • 左节点为空，右节点不为空，不对称，return false
  • 左不为空，右为空，不对称 return false
  • 左右都为空，对称，返回true

② 单层递归的逻辑

         单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

  • 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
  • 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
  • 如果左右都对称就返回 true ，有一侧不对称就返回 false 。
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool compare(TreeNode* left, TreeNode* right) {// 判断条件if (left == nullptr && right != nullptr) return false;else if (left != nullptr && right == nullptr) return false;else if (left == nullptr && right == nullptr) return true;else if (left->val != right->val) return false;bool outside = compare(left->left, right->right);   // 外层判断bool inside = compare(left->right, right->left);    // 内层判断return (outside && inside);}bool isSymmetric(TreeNode* root) {// 递归法if (root == nullptr) return true;return compare(root->left, root->right);}
};

（2）迭代法

        通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {if (root == nullptr) return true;queue<TreeNode*> que;que.push(root->left);que.push(root->right);while (!que.empty()) {TreeNode* leftnode = que.front(); que.pop();TreeNode* rightnode = que.front(); que.pop();if (leftnode == nullptr && rightnode != nullptr) return false;else if (leftnode != nullptr && rightnode == nullptr) return false;else if (leftnode == nullptr && rightnode == nullptr) continue;else if (leftnode->val != rightnode->val) return false;// 填入数据que.push(leftnode->left);que.push(rightnode->right);que.push(leftnode->right);que.push(rightnode->left);}return true;}
};

5. 二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/maximum-depth-of-binary-tree/description/

        给定一个二叉树 root ，返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：3示例 2：
输入：root = [1,null,2]
输出：2
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {// 二叉树层序遍历queue<TreeNode*> que;int depth = 0;if (root == NULL) return depth;que.push(root);while(!que.empty()) {int size = que.size();depth++; // 记录深度for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return depth;}
};

6. 二叉树的最小深度

111. 二叉树的最小深度 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/minimum-depth-of-binary-tree/description/

        给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

        说明：叶子节点是指没有子节点的节点。

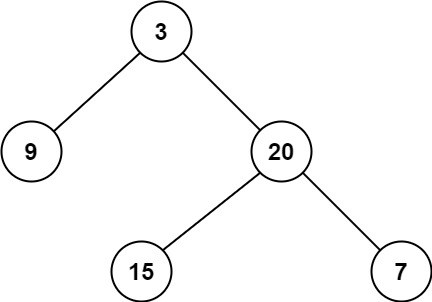
示例 1：
​​​​​​​输入：root = [3,9,20,null,null,15,7]
输出：2示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {// 层序遍历int depth = 0;queue<TreeNode*> que;if (root == NULL) return 0;que.push(root);while(!que.empty()) {int size = que.size();depth++; // 记录最小深度for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (node->left) que.push(node->left);if (node->right) que.push(node->right);if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出return depth;}}}return depth;}
};

7. 平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/balanced-binary-tree/description/

        给定一个二叉树，判断它是否是 平衡二叉树。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：true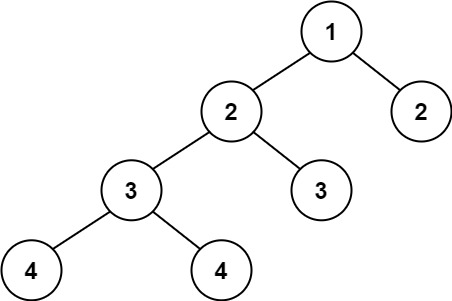

示例 2：
​​​​​​​输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
示例 3：
输入：root = []
输出：true

  思路：

（1）明确递归函数的参数 和 返回值

        参数：当前传入节点。         返回值：以当前传入节点为根节点的树的高度。

        如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。

（2）明确终止条件

        递归的过程中 依然是遇到 空节点了为终止，返回 0，表示 当前节点为 根节点的 树高度为0。

（3）明确单层递归的逻辑

        分别求出其左右子树的高度，然后如果差值小于 等于1，则返回当前二叉树的高度，否则返回-1，表示已经 不是二叉平衡树了。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int getHeight(TreeNode* node) {     // 后序遍历if (node == nullptr) return 0;int leftNum = getHeight(node->left);if (leftNum == -1) return -1;int rightNum = getHeight(node->right);if (rightNum == -1) return -1;// 子树拥有的层数越多，高度越高return abs(leftNum - rightNum) > 1 ? -1 : 1 + max(leftNum, rightNum);}bool isBalanced(TreeNode* root) {// 回溯法return getHeight(root) == -1 ? false : true;}
};

8. 二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-paths/description/

        给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。

示例 1：
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]示例 2：
输入：root = [1]
输出：["1"]

（1）回溯法

        这道题目要求 从根节点到叶子的路径，所以需要 前序遍历，这样才 方便让父节点 指向孩子 节点，找到 对应的路径。我们 要把路径 记录下来，需要 回溯来回退一个 路径 再进入另一个路径。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void TreePath(TreeNode* node, vector<string>& path, string str) {str = str + to_string(node->val);if (!node->left && !node->right) {path.push_back(str);return;}if (node->left) TreePath(node->left, path, str + "->");if (node->right) TreePath(node->right, path, str + "->");}vector<string> binaryTreePaths(TreeNode* root) {// 前序遍历vector<string> result;if (root == nullptr) return result;TreePath(root, result, "");return result;}
};

（2）迭代法

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> binaryTreePaths(TreeNode* root) {stack<TreeNode*> treeSt;// 保存树的遍历节点stack<string> pathSt;   // 保存遍历路径的节点vector<string> result;  // 保存最终路径集合if (root == NULL) return result;treeSt.push(root);pathSt.push(to_string(root->val));while (!treeSt.empty()) {TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中string path = pathSt.top();pathSt.pop();    // 取出该节点对应的路径if (node->left == NULL && node->right == NULL) { // 遇到叶子节点result.push_back(path);}if (node->right) { // 右treeSt.push(node->right);pathSt.push(path + "->" + to_string(node->right->val));}if (node->left) { // 左treeSt.push(node->left);pathSt.push(path + "->" + to_string(node->left->val));}}return result;}
};

相关文章：

【算法篇】二叉树类（1）（笔记）

目录 一、认识二叉树 1. 二叉树的种类 &#xff08;1&#xff09;满二叉树 &#xff08;2&#xff09;完全二叉树 &#xff08;3&#xff09;二叉搜索树 &#xff08;4&#xff09;平衡二叉搜索树 2. 二叉树的存储方式 3. 二叉树的遍历方式 4. 二叉树的定义 二、Leet…...

编程日记 2024/9/27 11:15:59

《C++无锁编程：解锁高性能并发的新境界》

在当今的软件开发领域&#xff0c;并发编程的重要性日益凸显。随着多核处理器的普及&#xff0c;开发者们越来越需要利用并发来提高程序的性能和响应速度。而 C作为一种强大的编程语言&#xff0c;提供了多种技术来实现无锁编程&#xff0c;从而在并发环境下获得更高的性能和更…...

编程日记 2024/9/27 11:14:58

系统架构设计师教程 第9章 9.5 软件可靠性测试 笔记

9.5 软件可靠性测试 ★★★☆☆ 9.5.1 软件可靠性测试概述 软件测试者可以使用很多方法进行软件测试&#xff0c;如按行为或结构来划分输入域的划分测试&#xff0c; 纯粹随机选择输入的随机测试&#xff0c;基于功能、路径、数据流或控制流的覆盖测试等。 软件可靠性测试由可…...

编程日记 2024/9/27 11:13:57

如何使用ssm实现校园体育赛事管理系统的设计与实现+vue

TOC ssm713校园体育赛事管理系统的设计与实现vue 绪论 课题背景 身处网络时代&#xff0c;随着网络系统体系发展的不断成熟和完善&#xff0c;人们的生活也随之发生了很大的变化。目前&#xff0c;人们在追求较高物质生活的同时&#xff0c;也在想着如何使自身的精神内涵得…...

编程日记 2024/9/27 11:11:55

CSS 中的文本相关属性（line - height、font、letter - 属性、text - 属性）

目录 非 VIP 用户可前往公众号回复“css”进行免费阅读 line - height属性 字号与行高的取值约定 行高与盒子高度的关系 font、letter -属性 、text -属性 font属性 letter -属性 text - 属性 非 VIP 用户可前往公众号回复“css”进行免费阅读 line - height属性 字号与…...

编程日记 2024/9/27 11:10:54

mobaxterm、vscode通过跳板机连接服务器

目标服务器&#xff1a;111.111.11.11 跳板机&#xff1a;100.100.10.10 1. mobaxterm通过跳板机连接服务器 1.1 目标服务器信息 1.2 跳板机信息 1.3 登录 点击登录&#xff0c;会输入密码&#xff0c;成功 参考&#xff1a;https://blog.csdn.net/qq_40636486/article/det…...

编程日记 2024/9/27 11:08:50

鸿萌数据恢复：iPhone 手机被盗后应采取哪些措施？警惕这些骗局

天津鸿萌科贸发展有限公司从事数据安全服务二十余年&#xff0c;致力于为各领域客户提供专业的数据恢复、数据备份解决方案与服务&#xff0c;并针对企业面临的数据安全风险&#xff0c;提供专业的相关数据安全培训。 丢失昂贵的 iPhone 不仅会造成较大的经济损失&#xff0c;还…...

编程日记 2024/9/27 11:06:48

为了学习Python熬夜部署了Jupyter Notebook 6.x

文章目录 Docker拉取并构建容器安装部署jupyter对Jupyter使用过程问题总结1 没有代码提示怎么办&#xff1f;2 如果想切换python版本了怎么办&#xff1f;3 想在jupyter里面使用vim怎么办&#xff1f; 遇见的问题参考文章 怎么说&#xff0c;今天在学习Python的时候&#xff0c…...

编程日记 2024/9/27 11:03:44

docker-文件复制（docker cp：用于在Docker主机和容器之间拷贝文件或目录）

文章目录 1、把宿主机的文件复制到容器内部1.1、查询 宿主机 root 下的文件1.2、docker cp /root/anaconda-ks.cfg spzx-redis:/root1.3、查看 spzx-redis 容器 中/root目录下是否有 anaconda-ks.cfg 文件 2、把容器中的文件 复制 到宿主机中2.1、查看 spzx-redis 容器 / 下的文…...

编程日记 2024/9/27 11:02:43

guava里常用功能

guava 是 Google 提供的一个 Java 库&#xff0c;提供了很多实用的工具类和方法&#xff0c;可以帮助开发者更高效地编写代码。以下是一些常用的 Guava 工具类及其功能示例&#xff1a; 1. Lists 用于操作列表的工具类。 import com.google.common.collect.Lists;List<In…...

编程日记 2024/9/27 11:01:42

su 命令：一键切换用户身份、提高su命令安全性的建议

一、命令简介 ​su ​命令是 Linux 和 Unix 系统中的一个实用工具&#xff0c;用于切换用户身份。它允许当前登录用户在不退出登录会话的情况下&#xff0c;切换到另一个用户的身份。通常&#xff0c;su ​用于从普通用户切换到 root 用户&#xff0c;或从 root 用户切换到其他…...

编程日记 2024/9/27 10:58:39

观察者模式（发布-订阅模式）

用途&#xff1a; &#xff08;1&#xff09;可用于拦截过滤器 &#xff08;2&#xff09;订单创建成功后的一些后续逻辑&#xff08;消息提醒&#xff0c;订单打印&#xff0c;物品打包等&#xff09; &#xff08;3&#xff09;需要由统一调度中心调度的一系列任务等 消息…...

编程日记 2024/9/27 10:57:38

耦合微带线单元的网络参量和等效电路公式推导

文档下载链接&#xff1a;耦合微带线单元的网络参量和等效电路资源-CSDN文库https://download.csdn.net/download/lu2289504634/89583027笔者水平有限&#xff0c;错误之处欢迎留言&#xff01; 一、耦合微带线奇偶模详细推导过程 二、2,4端口开路 三、2端口短路、3端口开路 四…...

编程日记 2024/9/27 10:56:37

elasticsearch的Ingest Attachment插件的使用总结

安装 Ingest Attachment 插件 确保 Elasticsearch 已安装&#xff1a; 首先&#xff0c;请确保你已经安装并运行了 Elasticsearch。可以通过访问 http://localhost:9200 来检查是否正常运行。 安装插件&#xff1a; 使用以下命令在 Elasticsearch 中安装 Ingest Attachment 插…...

编程日记 2024/9/27 10:55:34

SemiDrive E3 MCAL 开发系列（4） – Gpt 模块的使用

一、 概述 本文将会介绍SemiDrive E3 MCAL GPT模块的基本配置&#xff0c;并且会结合实际操作的介绍&#xff0c;帮助新手快速了解并掌握这个模块的使用&#xff0c;文中的 MCAL 是基于 PTG3.0 的版本&#xff0c;开发板是官方的 E3640 网关板。 二、 Gpt 模块的主要配置 …...

编程日记 2024/9/27 10:54:33

前端导出页面PDF

import html2canvas from html2canvas import { jsPDF } from jspdf import { Loading } from element-ui let downloadLoadingInstance// 导出页面为PDF格式---使用插件html2canvas和jspdf插件 export function exportPDF(fileName, node) {downloadLoadingInstance Loading.…...

编程日记 2024/9/27 10:53:32

Jenkins的安装

1.简介 官网&#xff1a;https://www.jenkins.io 中文文档&#xff1a;Jenkins Jenkins 是一个开源的持续集成&#xff08;CI&#xff09;工具&#xff0c;用于自动化构建、测试和部署软件项目。它提供了一个易于使用和可扩展的平台&#xff0c;帮助团队更高效地开发和交付软…...

编程日记 2024/9/27 10:52:31

初学51单片机之I2C总线与E2PROM

首先先推荐B站的I2C相关的视频I2C入门第一节-I2C的基本工作原理_哔哩哔哩_bilibili 看完视频估计就大概知道怎么操作I2C了&#xff0c;他的LCD1602讲的也很不错&#xff0c;把数据建立tsp和数据保持thd&#xff0c;比喻成拍照时候的摆pose和按快门两个过程&#xff0c;感觉还是…...

编程日记 2024/9/27 10:50:29

C语言数组探秘：数据操控的艺术【下】

承接上篇&#xff0c;我们继续讲数组的内容。 八.二维数组的使用 当我们掌握了二维数组的创建和初始化&#xff0c;那我们怎么使用二维数组呢&#xff1f;其实二维数组访问也是使用下标的形式的&#xff0c;二维数组是有行和列的&#xff0c;只要锁定了行和列就能唯一锁定数组中…...

编程日记 2024/9/27 10:49:28

Jmeter关联，断言，参数化

目录 一、关联 边界提取器 JSON提取器 正则表达式提取器 跨线程关联 二、断言 响应断言 JSON断言 断言持续时间 三、参数化 用户参数 csv data setconfig csvread函数 一、关联 常用的关联有三种 1.边界提取器 2.JSON提取器 3.正则表达式提取器 接下来就详细讲述…...

编程日记 2024/9/27 10:48:27

uniapp 对接腾讯云IM群组成员管理（增删改查）

UniApp 实战&#xff1a;腾讯云IM群组成员管理&#xff08;增删改查&#xff09; 一、前言 在社交类App开发中&#xff0c;群组成员管理是核心功能之一。本文将基于UniApp框架&#xff0c;结合腾讯云IM SDK&#xff0c;详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

编程新知 2026/1/13 9:59:27

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中，手势开发全攻略：

在 HarmonyOS 应用开发中&#xff0c;手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力&#xff0c;既支持点击、长按、拖拽等基础单一手势的精细控制&#xff0c;也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档&#xff0c…...

编程新知 2025/9/19 4:31:58

将对透视变换后的图像使用Otsu进行阈值化，来分离黑色和白色像素。这句话中的Otsu是什么意思？

Otsu 是一种自动阈值化方法&#xff0c;用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理&#xff0c;能够自动确定一个阈值&#xff0c;将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

编程新知 2026/1/9 19:36:58

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题&#xff1a;3564. 季节性销售分析 题目&#xff1a; 表&#xff1a;sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2025/10/5 19:58:27

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。

1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj&#xff0c;再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

编程新知 2026/2/5 4:21:48

Java毕业设计：WML信息查询与后端信息发布系统开发

JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发&#xff0c;实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构&#xff0c;服务器端使用Java Servlet处理请求&#xff0c;数据库采用MySQL存储信息&#xff0…...

编程新知 2025/10/27 13:29:11

接口自动化测试：HttpRunner基础

相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具&#xff0c;支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议&#xff0c;涵盖接口测试、性能测试、数字体验监测等测试类型…...

编程新知 2026/1/29 7:31:17

pycharm 设置环境出错

pycharm 设置环境出错 pycharm 新建项目&#xff0c;设置虚拟环境&#xff0c;出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

编程新知 2026/1/16 15:03:10

WebRTC调研

WebRTC是什么&#xff0c;为什么&#xff0c;如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

编程新知 2026/2/7 1:08:45