Leetcode 162.寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
思路:寻找峰值,最大值就一定是峰值,但这样遍历是行不通的,复杂度就到了O(n),所以每次操作必须寻找减小范围的方法,其核心就是找到规律,该题必有峰值,因为边界是无限小,而且一个节点左右节点都是不相同的,一个节点的峰值情况,无非三种情况,左小右小,那么该值就是峰值,左小右大,那么峰值必在右边因为有上升就必然会下降,最坏情况就是到边界下降到无穷小。所以按此规律,可以直接进行范围缩小。代码如下:和基本二分类似。
class Solution {public int findPeakElement(int[] nums) {// 由于数组边界是无穷小,所以一个元素i,如果i大于两侧,那么他就是峰值// 如果右侧大于i,右侧就必有峰值,左侧同理,这种情况就可以使用二分思想int leftIndex = 0;int rightIndex = nums.length - 1;while (true) {int middleIndex = (leftIndex + rightIndex) / 2;if (compare(nums, middleIndex, middleIndex-1) && compare(nums, middleIndex, middleIndex+1)) {return middleIndex; } else if (nums[middleIndex+1] > nums[middleIndex]) {leftIndex = middleIndex + 1;} else {rightIndex = middleIndex - 1;}}}// 由于数据中可能会有int的最小值,所以必须写比较函数public boolean compare(int[] nums, int index1, int index2) {if (index1 < 0 || index1 >= nums.length) {return false;}if (index2 < 0 || index2 >= nums.length) {return true;}return getNum(index1, nums) > getNum(index2, nums);}public int getNum(int index, int[] nums) {return nums[index];}
}
相关文章:

Leetcode 162.寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。 你可以假设 nums[-1] nums[n] -∞ 。 你必须实现时间复杂度为 O(…...

c语言:知识补充
c语言中编译开始会对#define,#include等内容做预处理,可以用#define写一些简单函数,方便使用 #include <stdio.h> #include <stdlib.h>#define MAX(A, B) ((A) > (B) ? (A) : (B))int main(){printf("%d\n", MAX(…...

Dapper介绍及特性
一、Dapper介绍及特性 Dapper是一个.NET平台上的轻量级对象关系映射(ORM)工具,它通过扩展IDbConnection接口,提供了一系列的扩展方法来执行SQL查询并将结果映射到.NET对象中。Dapper以其高性能和简单易用著称,特别适合…...

LeetCode 149. 直线上最多的点数
LeetCode 149. 直线上最多的点数 给你一个数组 points ,其中 points[i] [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。 示例 1: 输入:points [[1,1],[2,2],[3,3]] 输出:3 示例 2: 输入&…...

案例研究丨国控星鲨利用DataEase释放数据潜能,重塑业务视野
国药控股星鲨制药(厦门)有限公司(以下简称为国控星鲨)始创于1952年,前身为厦门鱼肝油厂,距今已经有70余年历史,是国家商务部认定的“中华老字号”企业。2011年,国药控股与厦门轻工集…...

网络基础概念和 socket 编程
网络基础概念和 socket 编程 学习目标: 了解 OSI 七层模型、TCP/IP 四层模型结构了解常见的网络协议格式掌握网络字节序和主机字节序之间的转换理解 TCP 服务器端通信流程理解 TCP 客户端通信流程实现 TCP 服务器端和客户端的代码 推荐一个非常好的学习资料仓库 协…...

TypeScript 中的接口、泛型与自定义类型
TypeScript 是一种超集语言,它为 JavaScript 添加了静态类型检查。通过 TypeScript,开发者可以获得更好的工具支持,并且能够编写出更加健壮的代码。本文将探讨 TypeScript 中的几个关键特性:接口、泛型以及如何创建自定义类型。 …...

常州威雅学校:跟随这场音乐盛宴,溯回她的音乐之路
时同学 常州威雅2021届毕业生 英国皇家北方音乐学院 钢琴系 西太湖畔清凉的晚风送来阵阵悦耳的钢琴声,时同学在母校的个人钢琴独奏悄然拉开序幕。这是她自毕业三年后,在常州威雅的首场钢琴独奏会。 随着第一个音符落下,她用手指在黑白键盘…...
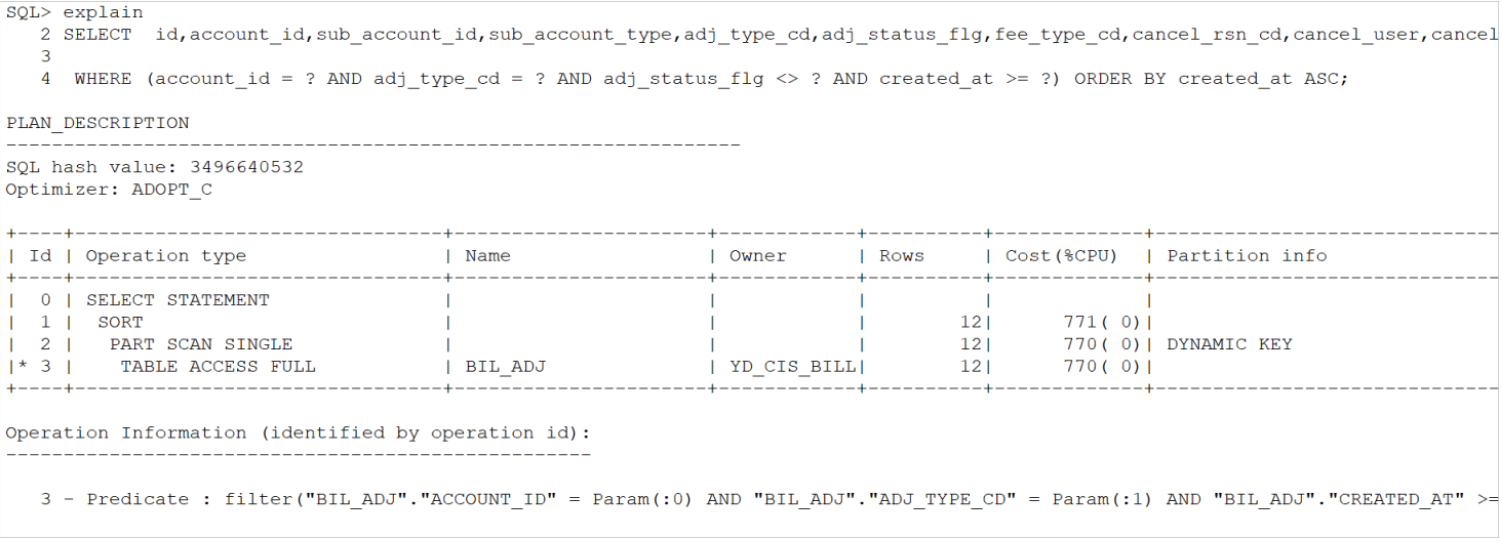
【YashanDB知识库】由于hist_head$中analyze time小于tab$中analyze time导致的sql语句执行慢
本文内容来自YashanDB官网,具体内容请见https://www.yashandb.com/newsinfo/7459465.html?templateId1718516 问题现象 某局点yashandb cpu使用率100%,经线上分析是由于几个sql执行慢,其中一个sql为简单的单行等值绑定变量过滤排序。 经分…...

【有啥问啥】深度理解主动学习:机器学习的高效策略
深度理解主动学习:机器学习的高效策略 在大数据时代,数据量的爆炸性增长与有限的标注资源之间的矛盾日益凸显。如何高效地利用标注资源来训练高质量的模型,成为了机器学习领域亟待解决的问题。主动学习(Active Learning, AL&…...

智能守护者X100 - 自动化生产线智能机器人安全监控管理系统
1.产品介绍 产品名称: 智能守护者X100 - 自动化生产线智能机器人安全监控管理系统 主要功能: 全方位实时监控:智能守护者X100采用高清摄像头与红外夜视技术,实现对自动化生产线及智能机器人的360无死角监控。系统能自动识别并追踪生产线上的机器人活动轨迹,确保生产安全…...

harmonyos面试题
你在项目中用过线程通信吗,线程是怎么进行通信的? 页面的生命周期有哪些? UAbility的生命周期呢? 你在项目中使用首选项主要用来数什么 组件通信的方式有息些 弹室UI是怎么在页面UI中使用的 常用的修饰符有愿些介绍一下 缓冲区是什么与16进制和数组有什么关…...

神经网络介绍及其在Python中的应用(一)
作者简介:热爱数据分析,学习Python、Stata、SPSS等统计语言的小高同学~ 个人主页:小高要坚强的博客 当前专栏:Python之机器学习 本文内容:神经网络介绍及其在Python中的线性回归应用 作者“三要”格言:要坚…...

数据流处理技术与Flink框架
一数据流 数据流定义: 数据流(Data Stream)是指数据以连续不断的方式到达和处理的序列。在现实世界中,许多数据来源都是以流的形式存在,比如: 1. 用户行为:用户在网站上的点击流、移动应用中…...

qt中QTatlewidget类常用操作表格的函数有哪些?
在Qt中,QTableWidget 类提供了丰富的函数来操作表格数据。以下是一些常用的操作表格的函数: 1. 初始化与配置 构造函数:QTableWidget(int rows, int columns, QWidget *parent nullptr):创建一个指定行数和列数的表格控件。设置…...

Linux上的C/C++编程
Linux上的C/C编程 yum软件包管理器Linux编辑器-vimvim命令模式指令集vim末行模式指令集 gcc/g的使用Linux自动化编译工具-make/MakefileLinux调试器-gdb调试命令 多人合作工具git yum软件包管理器 yum 是Linux上常用的包管理器,类似于Windows上的“应用商店”。 语…...
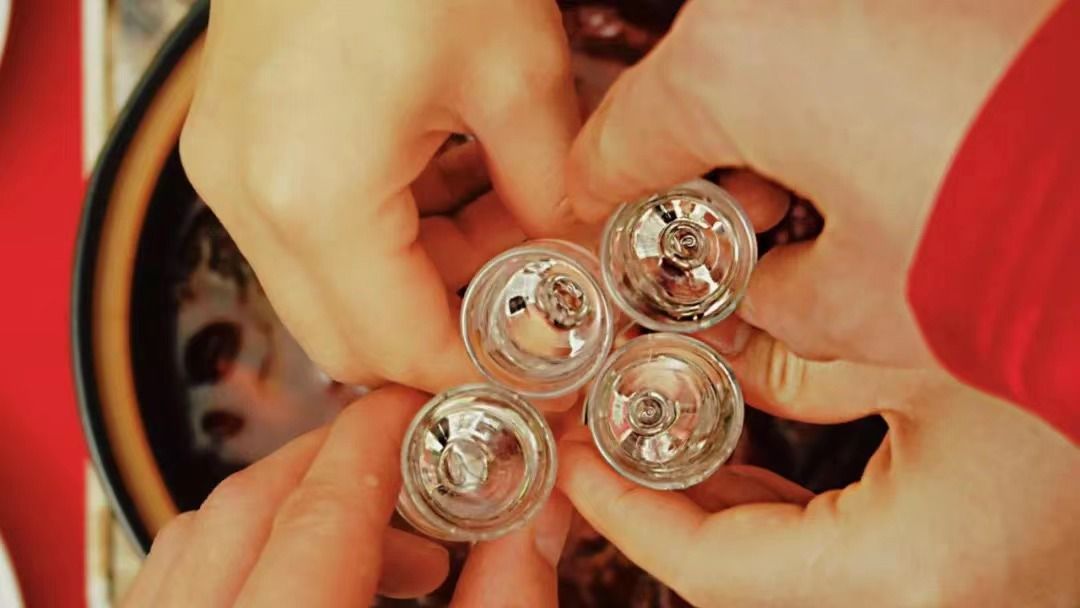
注意 秋季饮酒的正确打开方式
选择合适的白酒1.秋季气候干燥,适合选择一些口感醇厚、温润的白酒。比如酱香型白酒,它具有浓郁的香气和醇厚的口感,能在秋季给你带来温暖的感觉。2.浓香型白酒也是不错的选择,香气扑鼻,口感绵甜,能为秋季增…...
Python如何配置环境变量详解
一、概述 前提:已安装 Python,如下图: 1.1 检查是否已配置成功(选) 1 2 3 4 5 1. 打开运行窗口 (1) 快捷键 : Win r,并输入 cmd (2) 直接输入: Python 2. 若有下列提示,即为 安装成功…...
--并发与竞争)
Linux驱动开发(速记版)--并发与竞争
第十八章 并发与竞争 18.1 并发与竞争 18.1.1 并发 早期计算机 CPU单核心时,由于 CPU执行速度快于I/O操作,常因等待 I/O而空闲。 为提高 CPU利用率,引入了并发执行理论。并发通过算法在CPU执行I/O等待时切换至其他任务,使多个任…...

AI赋能,数字技术服务平台促进产业协同发展
在当今数字化浪潮席卷全球的时代,数字技术服务平台应运而生,成为推动各行业发展的强大引擎。数字技术服务平台是一个汇聚了众多先进数字技术和资源的综合性服务体系。它就像是一个功能强大的百宝箱,为用户提供了全方位的数字技术支持。 在这…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...
