C~排序算法

        在C/C++中，有多种排序算法可供选择，每种算法都有其特定的应用场景和特点。下面介绍几种常用的排序算法，包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序，并给出相应的示例代码和解释。

冒泡排序（Bubble Sort）

原理：通过重复遍历要排序的数列，比较相邻两个元素，如果它们的顺序错误（如从大到小、首字母从A到Z）就交换它们的位置，直到没有再需要交换的元素为止。

注意事项：冒泡排序简单但效率较低，适合小数据量排序。希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
• 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

算法流程：设数组的长度为 n ；

• 首先，对 n 个元素执行“冒泡”，将数组的最大元素交换至正确位置。
• 接下来，对剩余 n-1 个元素执行“冒泡”，将第二大元素交换至正确位置。
• 以此类推，经过 n-1 轮“冒泡”后，前 n-1 大的元素都被交换至正确位置。
• 仅剩的一个元素必定是最小元素，无须排序，因此数组排序完成。

冒泡排序的步骤如图所示：

示例：

#include <stdio.h>    // 冒泡排序函数，接受一个整数数组arr和数组的长度n作为参数  
void bubbleSort(int arr[], int n) 
{    int i, j, temp;    // 外层循环遍历数组，每完成一次遍历，最大的元素就会"冒泡"到它应该在的位置  for (i = 0; i < n-1; i++) {   // 内层循环负责进行相邻元素的比较和交换，确保每次遍历后，最大的元素位于其最终位置  // 由于每完成一次外层循环，最大的元素就已经排好，所以内层循环的次数可以减少  for (j = 0; j < n-i-1; j++) {   // 如果当前元素大于它后面的元素，则交换它们  if (arr[j] > arr[j+1]) {   temp = arr[j];  // 使用临时变量temp来交换两个元素  arr[j] = arr[j+1];  arr[j+1] = temp;  }  }  }  
}  int main() 
{    int arr[] = {64, 34, 25, 12, 22, 11, 90};  // 待排序的数组  int n = sizeof(arr)/sizeof(arr[0]);  // 计算数组的长度  bubbleSort(arr, n);  // 调用冒泡排序函数对数组进行排序  printf("Sorted array: \n");  for (int i = 0; i < n; i++)  // 遍历排序后的数组并打印每个元素  printf("%d ", arr[i]);  printf("\n");  // 换行  return 0;  // 程序正常结束  
}

补充：

• 外循环条件 i < n-1：这个条件确保了外循环遍历数组的次数足够多，以便将最大的元素冒泡到数组的末尾。由于冒泡排序每次遍历都会将一个最大的元素放到它最终的位置上，所以需要进行n-1次遍历来确保整个数组都被排序。为什么是n-1而不是n呢？因为当进行到第n-1次遍历后，最大的元素已经位于数组的最后一个位置，此时无需再进行第n次遍历，因为已经没有元素可以与之交换了。
• 内循环条件 j < n-i-1：这个条件确保了内循环在每次外循环迭代中只比较未排序部分的元素。随着外循环的进行，数组的最大元素逐渐被冒泡到末尾，因此未排序部分的长度逐渐减少。具体来说，随着i的增加，每次外循环结束时，数组末尾的i+1个元素都已经是排序好的了（即它们位于它们最终的位置上）。因此，在每次外循环的迭代中，内循环只需要比较和交换剩下的n-i-1个元素。换句话说，n-i-1表示的是在当前外循环迭代中，未排序部分的长度。由于内循环负责在这部分未排序的元素中进行比较和交换，所以它的边界条件就是j < n-i-1。

选择排序（Selection Sort）

原理：在要排序的一组数中，选出最小（或最大）的一个数与第一个位置的数交换；然后在剩下的数当中再找最小（或最大）的与第二个位置的数交换，依次类推，直到第n个元素和第n个元素比较为止。

注意事项：选择排序是不稳定的，适用于数据规模不大的情况。

算法流程：设数组的长度为 n

• 初始状态下，所有元素未排序，即未排序（索引）区间为 [0,n-1]。
• 选取区间 [0,n-1] 中的最小元素，将其与索引 0 处的元素交换。完成后，数组前 1 个元素已排序。
• 选取区间 [1,n-1]中的最小元素，将其与索引 1 处的元素交换。完成后，数组前 2 个元素已排序。
• 以此类推。经过 n-1 轮选择与交换后，数组前 n-1 个元素已排序。
• 仅剩的一个元素必定是最大元素，无须排序，因此数组排序完成。

选择排序的算法流程如图所示:

示例：

#include <stdio.h>  void selectionSort(int arr[], int n)   
{  int i, j, minIndex, temp;  // 外层循环控制从数组的第一个元素开始，到倒数第二个元素结束  // 因为当只剩下一个元素时，它自然就是排序好的  for (i = 0; i < n - 1; i++)   {  // 初始化最小值的索引为当前循环的起始位置  minIndex = i;  // 内层循环用于在未排序的部分找到最小值的索引  for (j = i + 1; j < n; j++)  // 如果发现更小的元素，则更新最小值的索引  if (arr[j] < arr[minIndex])  minIndex = j;  // 如果最小值不是当前循环的起始元素（即i指向的元素），则交换它们  // 这样，每次循环结束时，arr[i]都是当前未排序部分的最小值  if (minIndex != i) { // 这一步是优化，加上可以提高效率（当最小值已在正确位置时避免不必要的交换）  temp = arr[minIndex];  arr[minIndex] = arr[i];  arr[i] = temp;  }  }  
}int main() 
{int arr[] = { 64, 34, 25, 12, 22, 11, 90 };int n = sizeof(arr) / sizeof(arr[0]);selectionSort(arr, n);printf("Sorted array: \n");for (int i = 0; i < n; i++)printf("%d ", arr[i]);printf("\n");return 0;
}

插入排序（Insertion Sort）

原理：与手动整理一副牌的过程非常相似，在未排序区间选择一个基准元素，在已排序序列中逐一比较大小，找到相应位置并插入。

注意事项：插入排序对于小数据量或部分有序的数据效率较高。

算法流程：设基准元素为 base ，我们需要将 "从目标索引到 base 之间" 的所有元素向右移动一位，然后将 base 赋值给目标索引。如下所示：

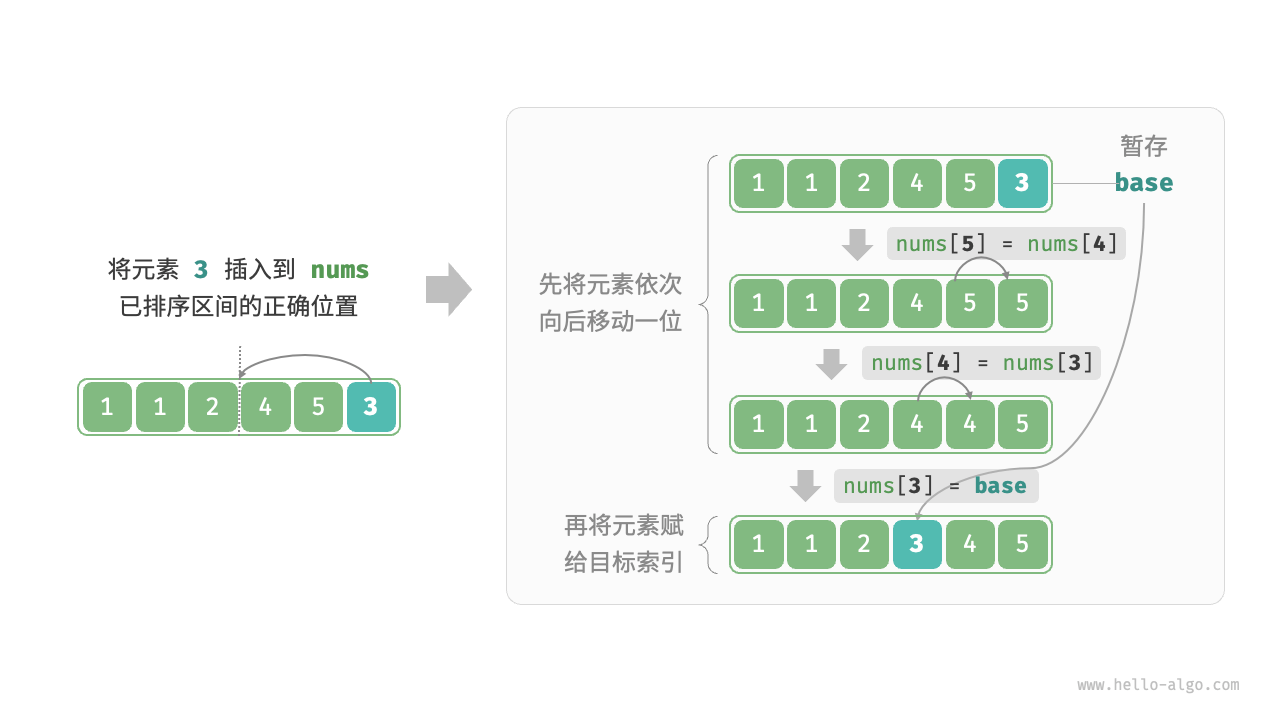
• 初始状态下，数组的第 1 个元素已完成排序。
• 选取数组的第 2 个元素作为 base ，将其插入到正确位置后，数组的前 2 个元素已排序。
• 选取第 3 个元素作为 base ，将其插入到正确位置后，数组的前 3 个元素已排序。
• 以此类推，在最后一轮中，选取最后一个元素作为 base ，将其插入到正确位置后，所有元素均已排序。

示例：

#include <stdio.h>  // 插入排序函数
void insertion_sort(int arr[], int len) 
{for (int i = 1; i < len; i++) {int temp = arr[i];  // 当前待插入的元素int j = i;// 向右移动大于temp的元素while (j > 0 && arr[j - 1] > temp) {arr[j] = arr[j - 1];j--;}arr[j] = temp;  // 插入元素到正确位置}
}// 主函数  
int main() 
{int arr[] = { 12, 11, 13, 5, 6 };int n = sizeof(arr) / sizeof(arr[0]);// 调用插入排序函数  insertionSort(arr, n);// 打印排序后的数组  printf("Sorted array: \n");for (int i = 0; i < n; i++)printf("%d ", arr[i]);printf("\n");return 0;
}

希尔排序（Shell Sort）

原理：是插入排序的一种更高效的改进版本。希尔排序通过将原来的数组分割成几个子序列来分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

注意事项：希尔排序的效率与增量序列的选择有很大关系。

算法流程：设数组的长度为 n

• 初始化增量序列，选择一个初始增量（gap），用于后续的分组和排序过程，通常是数组长度的一半（例如，gap = n / 2）。
• 逐步缩小增量，通过外层循环，每次迭代将增量减小（通常是减半，或者按照某种递减方式，例如gap = gap / 3 + 1）。
• 当增量减小至1时，整个数组将只被分为一组，此时进行最后一次插入排序。
• 在每一轮的增量下，通过内层循环对元素进行分组，每组包含相隔一定间隔（即当前增量）的元素。对每个小组内的元素使用插入排序算法进行排序，使在每个小组内部实现局部有序。
• 重复上述步骤，直到增量为1，随着增量的逐步减小，元素的分组越来越细，排序的范围也越来越广，直到最后整个数组通过插入排序完全有序。
• 完成排序，当增量减小至1时，整个序列已经基本有序，最后进行一次插入排序，完成整个排序过程。

希尔排序的步骤如图所示：

示例：

#include <stdio.h>  // 希尔排序函数  
void shell_sort(int arr[], int len) 
{  // 从数组长度的一半开始，每次循环将增量减半，直到增量为1  for (int gap = len / 2; gap > 0; gap /= 2) {  // 对每个间隔为gap的子序列进行插入排序  for (int i = gap; i < len; i++) {  // 取出当前子序列的第一个元素（实际上是每个间隔为gap的元素）  int temp = arr[i];  // 当前待插入的元素  int j = i;  // 移动当前间隔内大于temp的元素，为temp找到正确的位置  // 注意这里的比较和移动是基于gap的，即间隔为gap的元素之间进行比较和移动  while (j >= gap && arr[j - gap] > temp) {  arr[j] = arr[j - gap]; // 将大于temp的元素向后移动gap个位置  j -= gap; // 继续向前比较  }  arr[j] = temp;  // 将temp插入到正确的位置  }  }  // 当增量为1时，整个数组已经基本有序，此时再进行一次插入排序即可得到完全有序的数组  // 但由于之前的步骤已经使得数组基本有序，所以这一步的插入排序会非常高效  
}int main() 
{  int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 }; // 待排序数组  int len = sizeof(arr) / sizeof(arr[0]);  // 计算数组长度  shell_sort(arr, len);  // 调用希尔排序函数对数组进行排序  // 打印排序后的数组  for (int i = 0; i < len; i++) {  printf("%d ", arr[i]);  }  return 0;  
} 

快速排序（Quick Sort）

原理：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

注意事项：快速排序的平均时间复杂度为O(n log n)，但最坏情况下为O(n^2)，这通常发生在基准值选择不当时。

算法流程：

• 选取数组最左端元素作为基准数，初始化两个指针 i 和 j 分别指向数组的两端。
• 设置一个循环，在每轮中使用 i（j）分别寻找第一个比基准数大（小）的元素，然后交换这两个元素。
• 循环执行步骤 2. ，直到 i 和 j 相遇时停止，最后将基准数交换至两个子数组的分界线。

快速排序的步骤如图所示：

示例：

主要思想是将数组分为两个子数组，一个包含所有小于基准值的元素，另一个包含所有大于等于基准值的元素。这个过程称为分区（partitioning）。然后，递归地对这两个子数组进行相同的操作，直到子数组的长度为0或1，这时它们已经自然有序。

#include <stdio.h>  // 交换两个整数的值  
void swap(int *x, int *y) 
{  int t = *x;  *x = *y;  *y = t;  
}  // 递归实现快速排序  
void quick_sort_recursive(int arr[], int start, int end) 
{  if (start >= end) // 如果起始位置大于等于结束位置，说明子数组长度为0或1，已经是有序的，直接返回  return;  // 选择最后一个元素作为基准值（pivot），但这里的选择不是最优的，因为可能会导致某些情况下性能不佳  int pivot = arr[end];  int left = start, right = end - 1;  // 分区过程：将数组分为小于基准值的左半部分和大于等于基准值的右半部分  while (left <= right) {  // 从左向右找到第一个大于等于基准值的元素  while (left <= right && arr[left] < pivot)  left++;  // 从右向左找到第一个小于基准值的元素  while (left <= right && arr[right] >= pivot)  right--;  // 如果left和right没有交错，交换它们指向的元素  if (left <= right)  swap(&arr[left], &arr[right]);  }  // 将基准值交换到中间位置，此时基准值左边都是小于它的，右边都是大于等于它的  swap(&arr[left], &arr[end]);  // 递归地对基准值左右两侧的子数组进行快速排序  quick_sort_recursive(arr, start, left - 1);  quick_sort_recursive(arr, left + 1, end);  
}  // 快速排序的入口函数，封装了对递归函数的调用  
void quick_sort(int arr[], int len) 
{  quick_sort_recursive(arr, 0, len - 1); // 从数组的第一个元素到最后一个元素进行排序  
}  int main() 
{  int arr[] = {22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70};  int len = sizeof(arr) / sizeof(arr[0]); // 计算数组的长度  quick_sort(arr, len); // 调用快速排序函数对数组进行排序  // 打印排序后的数组  for (int i = 0; i < len; i++) {  printf("%d ", arr[i]);  }  return 0;  
}

 归并排序（Merge Sort）

原理：归并排序是一种分而治之的算法，它将一个大数组分成两个小数组，对这两个小数组分别进行排序，然后将排序好的小数组合并成一个大的有序数组。这个过程递归地进行，直到数组被分成只有一个元素的子数组（此时子数组自然是有序的），然后开始合并过程。

注意事项：归并排序是稳定的排序方法，但空间复杂度较高，为O(n)。

算法流程：

1. 划分（Divide）：通过递归不断地将数组从中点处分开，即找到中间位置mid，将数组分为左右两个子数组。递归地对左右两个子数组进行排序。
2. 递归终止条件（Base Case）：如果子数组的大小为1，则认为它是已经排序好的，因为只有一个元素的数组自然是有序的。
3. 合并（Merge）：当子数组长度为 1 时终止划分，开始合并，持续地将左右两个较短的有序数组合并为一个较长的有序数组，直至结束。

假设有两个已经排序的子数组A和B，将它们合并成一个有序的大数组C：

• 初始化三指针：i 指向A的开始，j 指向B的开始，k 指向C的开始。
• 比较A[i]和B[j]的大小：如果A[i] <= B[j]，则将A[i]复制到C[k]，然后i和k都向后移动一位。否则，将B[j]复制到C[k]，然后j和k都向后移动一位。
• 重复上述过程，直到其中一个子数组的所有元素都被复制。
• 如果A中还有剩余元素，将它们全部复制到C的末尾（因为B中的所有元素都已经被复制且有序，所以A中剩余的元素也都大于B中所有元素，可以直接复制）。

• 同理，如果B中还有剩余元素，也直接复制到C的末尾（但在归并排序的通常实现中，这一步是多余的，因为A和B的合并会覆盖整个C，不会有剩余）。

归并排序的步骤如图所示：

示例：

#include <stdio.h>  // 引入标准输入输出库，用于打印结果  
#include <stdlib.h> // 引入标准库，用于动态内存分配和程序退出  
#include <string.h> // 引入字符串处理库，虽然本例中未直接使用，但常见于C程序  // 函数声明  
void merge_sort_recursive(int arr[], int reg[], int start, int end);  // 递归实现归并排序  
void merge_sort(int arr[], const int len);  // 归并排序入口函数  int main()   
{    int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };  // 定义并初始化一个整数数组  int len = sizeof(arr) / sizeof(arr[0]);  // 计算数组的长度  merge_sort(arr, len);  // 调用归并排序函数对数组进行排序  // 打印排序后的数组  for (int i = 0; i < len; i++)   {    printf("%d ", arr[i]);  // 逐个打印数组元素  }    printf("\n");  // 在数组元素打印完毕后换行  return 0;  // 程序正常结束  
}    // 递归实现归并排序  
void merge_sort_recursive(int arr[], int reg[], int start, int end)   
{    if (start >= end)  // 如果当前处理的数组部分只有一个元素或为空，则直接返回  return;    int mid = start + (end - start) / 2;  // 找到当前处理部分的中间位置  int start1 = start, end1 = mid;       // 定义左半部分的起始和结束索引  int start2 = mid + 1, end2 = end;     // 定义右半部分的起始和结束索引  merge_sort_recursive(arr, reg, start1, end1);  // 递归排序左半部分  merge_sort_recursive(arr, reg, start2, end2);  // 递归排序右半部分  // 合并左右两部分到临时数组reg中  int k = start;  // 定义临时数组的索引  while (start1 <= end1 && start2 <= end2)   {    reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];    // 比较左右两部分当前元素，将较小者放入临时数组，并移动相应指针  }    while (start1 <= end1)   {    reg[k++] = arr[start1++];  // 将左半部分剩余元素放入临时数组  }    while (start2 <= end2)   {    reg[k++] = arr[start2++];  // 将右半部分剩余元素放入临时数组  }    // 将排序好的部分复制回原数组arr中  memcpy(arr + start, reg + start, (end - start + 1) * sizeof(int));    // 使用memcpy函数高效地将临时数组中的排序结果复制回原数组  
}    // 归并排序入口函数  
void merge_sort(int arr[], const int len)   
{    int* reg = (int*)malloc(len * sizeof(int));  // 为临时数组reg分配内存  if (reg == NULL)   {  // 检查内存分配是否成功  fprintf(stderr, "Memory allocation failed\n");  // 如果内存分配失败，则打印错误信息  exit(EXIT_FAILURE);  // 并以异常状态退出程序  }    merge_sort_recursive(arr, reg, 0, len - 1);  // 对整个数组进行归并排序  free(reg);  // 释放临时数组reg所占用的内存  
}