106. 从中序与后序遍历序列构造二叉树
文章目录
- 106. 从中序与后序遍历序列构造二叉树
- 思路
- 105. 从前序与中序遍历序列构造二叉树
- 思路
- 思考
106. 从中序与后序遍历序列构造二叉树
106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和postorder,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
- 1 <= inorder.length <= 3000
- postorder.length == inorder.length
- -3000 <= inorder[i], postorder[i] <= 3000
- inorder 和 postorder 都由 不同 的值组成
- postorder 中每一个值都在 inorder 中
- inorder 保证是树的中序遍历
- postorder 保证是树的后序遍历
思路
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,然后根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:

那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
不难写出如下代码:(先把框架写出来)
注意:以下代码中ir,il,pr,pl 分别表示中序和后序数组的左右区间,左闭右开
// 第一步
if ir - il == 0 {return nil }if ir - il == 1 {return &TreeNode{Val:postorder[pr-1]}}// 第二步:后序遍历数组最后一个元素,就是当前的中间节点val := postorder[pr - 1]curTreeNode := &TreeNode{Val:val}// 第三步:找切割点idx := 0for i := il;i < ir;i++ {if inorder[i] == val {idx = ibreak}}// 第四步:切割中序数组,得到 中序左数组和中序右数组// 第五步:切割后序数组,得到 后序左数组和后序右数组// 第六步 递归构造左右子树,拼接为当前节点的左右子树curTreeNode.Left = dfs(inorder,il,idx,postorder,pl,pl + idx - il)curTreeNode.Right = dfs(inorder,idx+1,ir,postorder,pl + idx - il,pr-1)return curTreeNode
难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。即从最入口的时候是左闭右开,则递归的过程中要一直遵循这个原则,这样区间才不会乱套。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必须要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
假设找到切割点在中序数组中的索引为idx,则中序数组切割后,左数组是[il,idx),即起点还是il,但是右边界是到idx,且不包含idx,因为idx是当前节点的数值,不可能出现在子树中的,这样[il,idx)符合了我们坚持的左闭右开原则。而中序数组的右边界则是[idx+1,ir),同样排除了idx,即当前递归层取出了中序数组中idx对应的数值构造了一个树节点。
curTreeNode.Left = dfs(inorder,il,idx,postorder,pl,pl + idx - il)
curTreeNode.Right = dfs(inorder,idx+1,ir,postorder,pl + idx - il,pr-1)
接下来就看看怎么切割后序数组。
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
后序数组的切割点怎么找?
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
因为左中序数组的元素个数为 idx - il个,所以左后序数组的元素也应该是 idx - il个,从而推断出左后序数组的区间为[pl,pl + idx - il) ,有个方便记忆的方法,中序左数组元素个数为idx - il,左后序数组的元素个数也是右区间减去左区间的,所有就是(pl + idx - il ) - pl = idx - il,即左后续数组的终止位置是 需要加上 中序区间的大小,而右后序区间则应该从pl + idx - il直到倒数第二个元素。
完整代码如下:
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func buildTree(inorder []int, postorder []int) *TreeNode {// 后序最后一个节点一定是根节点,找到根节点后,可以切割中序的左右子树,并切割后续的左右子树// 而后递归构造左右子树即可if len(postorder) == 0 {return nil}root := dfs(inorder,0,len(inorder),postorder,0,len(postorder))return root
}func dfs(inorder []int,il ,ir int,postorder []int,pl,pr int) *TreeNode {if ir - il == 0 {return nil }if ir - il == 1 {return &TreeNode{Val:postorder[pr-1]}}val := postorder[pr - 1]curTreeNode := &TreeNode{Val:val}idx := 0for i := il;i < ir;i++ {if inorder[i] == val {idx = ibreak}}curTreeNode.Left = dfs(inorder,il,idx,postorder,pl,pl + idx - il)curTreeNode.Right = dfs(inorder,idx+1,ir,postorder,pl + idx - il,pr-1)return curTreeNode
}

105. 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组preorder和inorder,其中preorder是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder 和 inorder 均 无重复 元素
- inorder 均出现在 preorder
- preorder 保证 为二叉树的前序遍历序列
- inorder 保证 为二叉树的中序遍历序列
思路
思路上上面106题一模一样,所以直接上代码吧!!
Go代码
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func buildTree(preorder []int, inorder []int) *TreeNode {if len(preorder) == 0 {return nil}root := dfs(preorder,0,len(preorder),inorder,0,len(inorder))return root
}func dfs(preorder []int,pl,pr int,inorder []int,il,ir int) *TreeNode {if pr - pl == 0 {return nil}if pr - pl == 1 {return &TreeNode{Val:preorder[pl]}}val := preorder[pl]curTreeNode := &TreeNode{Val:val}var idx intfor i,num := range inorder {if num == val {idx = ibreak}}// 中序的切割容易,前序的切割则遵循长度和中序一致就比较容易确定了,如左中序变为il,idx,则长度是idx - il// 左前序的起点是pl+1无疑,区间长度需要是idx-il,从而确定左前序右边界为pl + 1 + idx - ilcurTreeNode.Left = dfs(preorder,pl + 1,pl + 1 + idx - il,inorder,il,idx)curTreeNode.Right = dfs(preorder,pl + 1 + idx - il ,pr,inorder,idx + 1,ir)return curTreeNode
}

思考
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
那么前序和后序可不可以唯一确定一棵二叉树呢?
前序和后序不能唯一确定一棵二叉树!,因为没有中序遍历无法确定左右部分,也就是无法分割。
举一个例子:
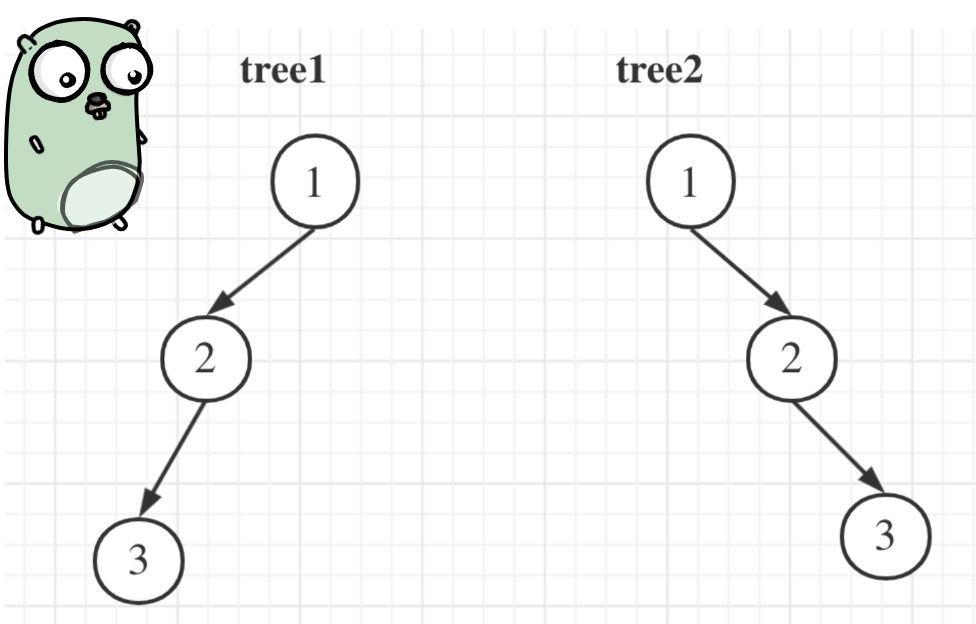
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和tree2的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一棵二叉树!
相关文章:

106. 从中序与后序遍历序列构造二叉树
文章目录 106. 从中序与后序遍历序列构造二叉树思路 105. 从前序与中序遍历序列构造二叉树思路 思考 106. 从中序与后序遍历序列构造二叉树 106. 从中序与后序遍历序列构造二叉树 给定两个整数数组 inorder 和postorder,其中 inorder 是二叉树的中序遍历ÿ…...

监控和日志管理:深入了解Nagios、Zabbix和Prometheus
在现代IT运维中,监控和日志管理是确保系统稳定性和性能的关键环节。本文将介绍三种流行的监控工具:Nagios、Zabbix和Prometheus,帮助您了解它们的特点、使用场景以及如何进行基本配置。 一、Nagios Nagios 是一个强大的开源监控系统&#x…...

Win10下载Python:一步步指南
Win10下载Python:一步步指南 在Win10操作系统中下载并安装Python可能是一项挑战性的任务,但是在本文中,我们将向您提供三个不同的方法,以便轻松地完成这项任务。 方法一:使用Microsoft Store Microsoft Store是一个…...

Race Karts Pack 全管线 卡丁车赛车模型素材
是8辆高细节、可定制的赛车,内部有纹理。经过优化,可在手机游戏中使用。Unity车辆系统已实施-准备驾驶。 此套装包含8种不同的车辆,每种车辆有8-10种颜色变化,总共有75种车辆变化! 技术细节: -每辆卡丁车模型使用4种材料(车身、玻璃、车轮和BrakeFlare) 纹理大小: -车…...

C#——switch案例讲解
案例:根据输入的内容判断执行哪一条输出语句 string number txtUserName.Text; switch(number) { case"101":MessageBox.Show("您进入了101房间");break; case"102":MessageBox.Show("您进入了102房间");break; case&quo…...

技术美术一百问(02)
问题 前向渲染和延迟渲染的流程 前向渲染和延迟渲染的区别 G-Buffer是什么 前向渲染和延迟渲染各自擅长的方向总结 GPU pipeline是怎么样的 Tessellation的三个阶段 什么是图形渲染API? 常见的图形渲染API有哪些? 答案 1.前向渲染和延迟渲染的流程 【例图…...

12 函数的应用
函数的应用 一、Shell递归函数 函数优点: 函数在程序设计中是一个非常重要的概念,它可以将程序划分成一个个功能相对独立的代码块,使代码的模块化更好,结构更加清晰,并可以有效地减少程序的代码量。 递归…...
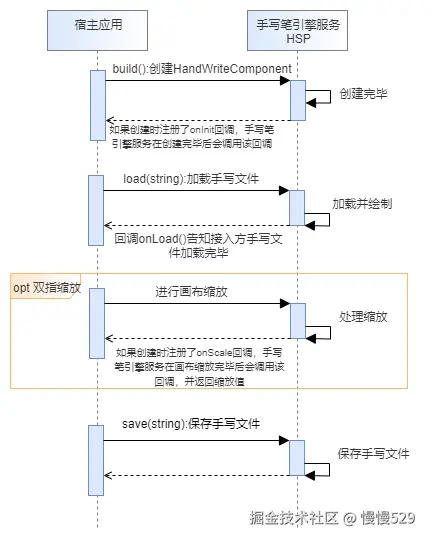
鸿蒙开发(NEXT/API 12)【硬件(接入手写套件)】手写功能开发
接入手写套件后,可以在应用中创建手写功能界面。界面包括手写画布和笔刷工具栏两部分,手写画布部分支持手写笔和手指的书写效果绘制,笔刷工具栏部分提供多种笔刷和编辑工具,并支持对手写功能进行设置。接入手写套件后将自动开启一…...
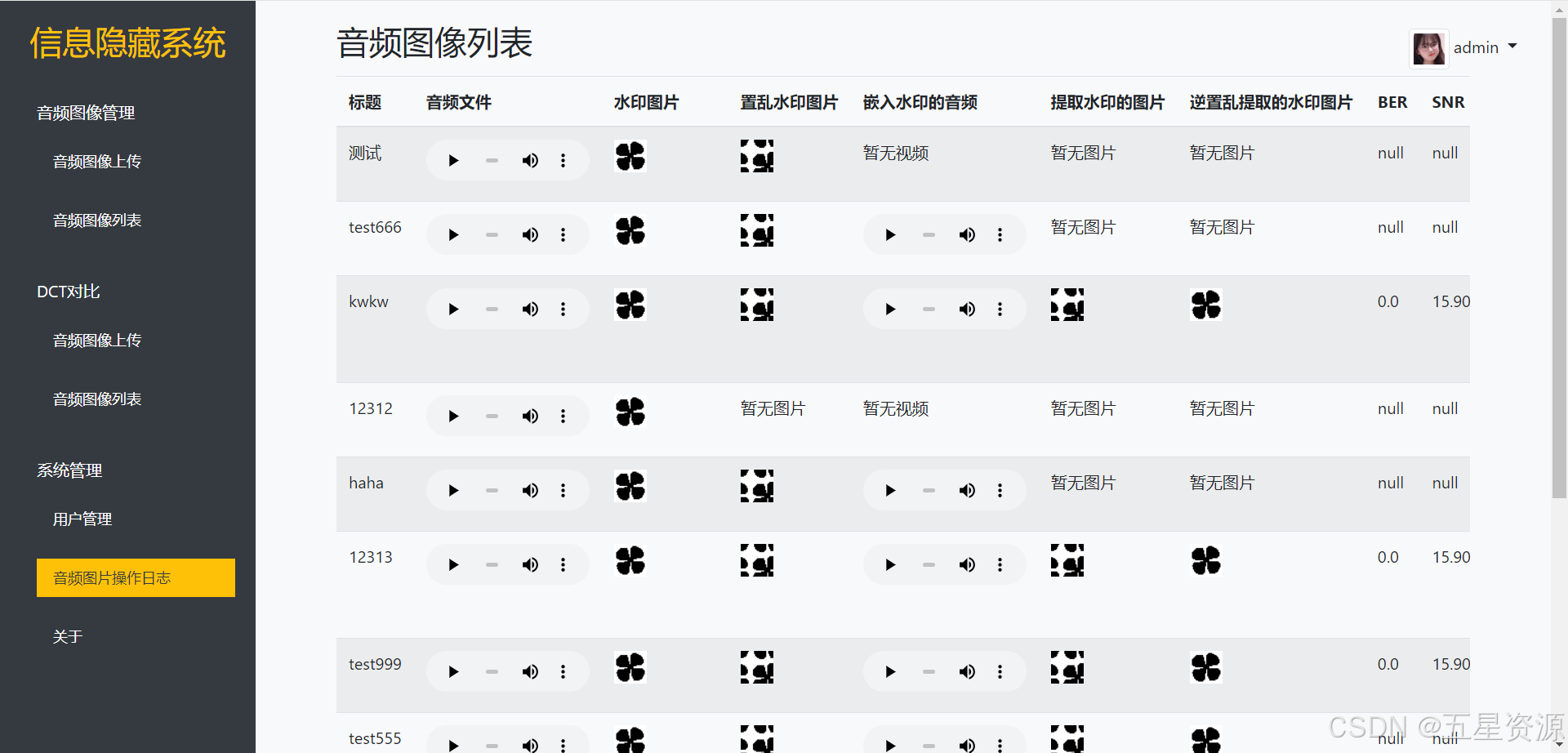
基于python+flask+mysql的音频信息隐藏系统
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

18724 二叉树的遍历运算
### 思路 1. **递归构建树**: - 先序遍历的第一个节点是根节点。 - 在中序遍历中找到根节点的位置,左边部分是左子树,右边部分是右子树。 - 递归构建左子树和右子树。 2. **递归生成后序遍历**: - 递归生成左子树的…...

代理模式简介:静态代理VS与动态代理
代理模式:静态代理VS动态代理 1、定义2、分类2.1 静态代理2.2 动态代理 3、使用场景4、总结 💖The Begin💖点点关注,收藏不迷路💖 1、定义 代理模式是一种设计模式,通过代理对象控制对目标对象的访问。简而…...

使用 Dockerfile 和启动脚本注册 XXL-Job 执行器的正确 IP 地址
解决方案:使用 Dockerfile 和启动脚本注册 XXL-Job 执行器的正确 IP 地址 在使用容器化方式注册 XXL-Job 执行器时,由于容器的 IP 地址是动态分配的,可能会导致调度中心无法访问执行器。为了解决这个问题,可以使用 Dockerfile 和…...

Python连接Kafka收发数据等操作
目录 一、Kafka 二、发送端(生产者) 三、接收端(消费者) 四、其他操作 一、Kafka Apache Kafka 是一个开源流处理平台,由 LinkedIn 开发,并于 2011 年成为 Apache 软件基金会的一部分。Kafka 广泛用于构…...

MySql在更新操作时引入“两阶段提交”的必要性
日志模块有两个redo log和binlog,redo log 是引擎层的日志(负责存储相关的事),binlog是在Server层,主要做MySQL共嗯那个层面的事情。redo log就像一个缓冲区,可以让当更新操作的时候先放redo log中…...

充气模块方案——无刷充气泵pcba方案
在方案开发中,充气效率是无刷充气泵PCBA方案开发中的关键问题。一般通过优化电路设计和控制算法,可以实现高效的气体压缩和快速的充气效果。另外,选择合理的电机驱动器和传感器等元器件能够提高打气泵的功率和效率,减少充气时间&a…...

[sql-03] 求阅读至少两章的人数
准备数据 CREATE TABLE book_read (bookid varchar(150) NOT NULL COMMENT 书籍ID,username varchar(150) DEFAULT NULL COMMENT 用户名,seq varchar(150) comment 章节ID ) ENGINEInnoDB DEFAULT CHARSETutf8mb4 COMMENT 用户阅读表insert into book_read values(《太子日子》…...

Linux如何通过链接下载文件
在Linux系统中,你可以通过多种方式通过链接下载文件。这些方式包括使用命令行工具(如wget、curl、axel等)和图形界面程序(如浏览器或文件管理器)。以下是几种常用的命令行方法: 1. 使用wget wget是一个非交…...

seL4 IPC(五)
官网链接:link 求解 代码中的很多方法例如这一个教程里面的seL4_GetMR(0),我在官方给的手册和API中都搜不到,想问一下大家这些大家都是在哪里搜的!! IPC seL4中的IPC和一般OS中讲的IPC概念相差比较大,根…...

【Java】多线程基础操作
多线程基础操作 Thread类回顾Thread类观察线程运行线程的休眠常用方法构造方法属性获取方法 中断线程线程状态线程等待 初识synchronized问题引入初步使用初步了解可重入锁死锁 volatile问题引入初步使用volatile 与 synchronized 线程顺序控制初步了解wait()notify()防止线程饿…...

基于Hive和Hadoop的病例分析系统
本项目是一个基于大数据技术的医疗病历分析系统,旨在为用户提供全面的病历信息和深入的医疗数据分析。系统采用 Hadoop 平台进行大规模数据存储和处理,利用 MapReduce 进行数据分析和处理,通过 Sqoop 实现数据的导入导出,以 Spark…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
