【抽代复习笔记】29-群(二十三):生成子群的两道例题及子群陪集的定义
例1:取S3的子集S = {(12),(123)},S的生成子群包含哪些元?一个群的两个不同的子集会不会生成相同的子群?
解:(1)S的生成子群就是S3。证明[有不理解之处可以回头看看第27篇笔记中生成子群的定义]:
任取m,n∈Z,对于m,当m为奇数时,(12)ᵐ = (12),当m为偶数时,(12)ᵐ = (1);
对于n,当n=3k时,(123)ⁿ = (1),当n=3k+1时,(123)ⁿ = (123),当n=3k+2时,(123)ⁿ = (132);
因此(12)ᵐ o (123)ⁿ的所有可能的值为:(1),(12),(123),(132),(13),(23)这6个,而这6个元素组成的集合正是S3,因此S的生成子群是S3。
(2)同一个群的两个不同的子集可能会生成相同的子群。例如:
设S' = {(13),(132)},则S'的生成子群也是S3(证明同(1)),(1)中的S和(2)中的S'都是群S3的子集,这说明同一个群的两个不同的子集可能会生成相同的子群。
(3)补充:同一个群的两个不同的子集也有可能生成不同的子群,例如:
{(12)}和{(13)}都是S3的子集,但两者的生成子群分别是{(1),(12)}和{(1),(13)},这说明同一个群的两个不同的子集也有可能生成不同的子群。
例2:H是G的非空子集,且H中每一个元素的阶均有限,试证:“H是G的子群”当且仅当“对任意的a,b∈H,都有a o b∈H”。
证明:必要性:根据子群的定义及第一判定定理,可知必要性显然是成立的。
充分性:若对任意的a,b∈H,都有a o b∈H,则当b=a时,有a^2∈H,由此可推出a^3,a^4,……∈H,
又H中每一个元素的阶都是有限的,因此设|a| = n,则a^n = e,从而a的逆元a^(-1) = e o a^(-1) = a^n o a^(-1) = a^(n-1)∈H,
因此根据子群的第一判定定理,可推导出H是G的子群。
子群的陪集
定义1:H是G的子群,且a∈G,则称aH = {ah|h∈H}(Ha = {ha|h∈H})为子群H的左陪集(右陪集);若aH = Ha,则称它们为子群的陪集。
例:已知克莱因四元群K₄ = {(1),(12)(34),(13)(24),(14)(23)}是四次交错群A₄的子群,即K₄⊆A₄,
(1)写出S₄中的所有成员;
(2)写出A₄中的所有成员;
(3)求(1)K₄,(123)K₄,(132)K₄;
(4)求K₄(1),K₄(123),K₄(132);
(5)比较第(3)问和第(4)问;
(6)求(124)K₄,(134)K₄,(12)(34)K₄,(14)(23)K₄。
解:(1)S₄ = {(1),(12),(13),(14),(23),(24),(34),(123),(132),(124),(142),(134),(143),(234),(243),(1234),(1243),(1324),(1342),(1423),(1432),(12)(34),(13)(24),(14)(23)};
(2)A₄ = {(1),(12)(34),(13)(24),(14)(23),(123),(132),(124),(142),(134),(143),(234),(243)};
(3)(1)K₄ = {(1),(12)(34),(13)(24),(14)(23)},(123)K₄ = {(123),(243),(142),(134)},(132)K₄ = {(132),(143),(234),(124)};
(4)K₄(1) = K₄,K₄(123) = {(123),(134),(243),(142)},K₄(132) = {(132),(234),(124),(143)};
(5)①不难发现:
(1)K₄∪(123)K₄∪(132)K₄ = A₄,这是A₄关于K₄的一个左陪集分解;
K₄(1)∪K₄(123)∪K₄(132) = A₄,这是A₄关于K₄的一个右陪集分解。
②经过比较,可发现(1)K₄ = K₄(1),(123)K₄ = K₄(123),(132)K₄ = K₄(132),即(1)K₄,(123)K₄,(132)K₄和K₄(1),K₄(123),K₄(132)都是K₄的陪集。
③经过比较可发现,(1)K₄,(123)K₄,(132)K₄和K₄(1),K₄(123),K₄(132)各自的元素个数和K₄一样,都是4,因此不难得出一个结论:左右陪集的阶与子群的阶相等,即:|aK₄| = |K₄a| = |K₄|。
(6)(124)K₄ = {(124),(234),(143),(132)},
(134)K₄ = {(134),(142),(243),(123)},
(12)(34)K₄ = {(12)(34),(1),(14)(23),(13)(24)},
(14)(23)K₄ = {(14)(23),(13)(24),(12)(34),(1)}。
(待续......)
相关文章:
:生成子群的两道例题及子群陪集的定义)
【抽代复习笔记】29-群(二十三):生成子群的两道例题及子群陪集的定义
例1:取S3的子集S {(12),(123)},S的生成子群包含哪些元?一个群的两个不同的子集会不会生成相同的子群? 解:(1)S的生成子群就是S3。证明[有不理解之处可以回头看看第27篇笔记中生成子群的定…...

安全防护装备检测系统源码分享
安全防护装备检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Computer…...

easyexcel常见问题分析
文章目录 一、读取数字多了很多小数位的精度问题 一、读取数字多了很多小数位的精度问题 浮点型转成BigDecimal的时候会出现精度问题,例如 这儿设置的实体类对象类型是String,默认用到的是StringNumberConverter转换器 2.1.4 版本 public class Strin…...

精通推荐算法31:行为序列建模之ETA — 基于SimHash实现检索索引在线化
1 行为序列建模总体架构 2 SIM模型的不足和为什么需要ETA模型 SIM实现了长周期行为序列的在线建模,其GSU检索单元居功至伟。但不论Hard-search还是Soft-search,都存在如下不足: GSU检索的目标与主模型不一致。Hard-search通过类目属性来筛选…...

Python知识点:如何使用Python进行卫星数据分析
开篇,先说一个好消息,截止到2025年1月1日前,翻到文末找到我,赠送定制版的开题报告和任务书,先到先得!过期不候! 如何使用Python进行卫星数据分析 卫星数据分析是地球观测领域的一项关键技术&a…...

Python实现Phong着色模型算法
目录 使用Python实现Phong着色模型算法引言Phong着色模型的基本原理1. 模型组成2. 公式 Phong着色模型的Python实现1. 向量类的实现2. 光源类的实现3. 材质类的实现4. Phong着色器类的实现 整体实现总结 使用Python实现Phong着色模型算法 引言 在计算机图形学中,光…...

异步框架 fastapi -- 连接mysql数据库
文章目录 docker部署mysqlfastapi连接mysql docker部署mysql 拉取mysql镜像 # 查看docker 服务状态 systemctl status docker systemctl start docker # 设置 开机启动 systemctl enable docker# 拉取mysql 镜像 docker search mysql:latest # 不指定版本时,默认…...

Spring 全家桶使用教程 —— 后端开发从入门到精通
Spring 全家桶是 Java 后端开发的利器,提供了从基础开发到复杂微服务架构的一整套解决方案。通过对各个 Spring 组件的掌握,开发者可以快速构建高效、稳定的企业级应用。本文将详细介绍 Spring 全家桶的各个组件,帮助开发者深入理解其核心功能…...

AI动漫转真人终极教程!3步做出爆款内容,音乐推广号变现
从小到大,我们看过的动漫、玩过的游戏有很多很多 但我们会发现里面的角色或者人物都是二次元的 我就会好奇这些动漫人物在现实中会长什么样 而现在,我们通过AI绘画竟然就能还原出来他们现实中的样子 除了动漫角色和游戏人物,古代的画像、…...

vue2 vconsole有助于移动端开发页面调试
项目场景: pc项目开发中,有浏览器自带的调试工具。但在移动端,就需要自己搭建调试工具了。vconsole一种非常方便的前端调试依赖库,有助于我们在移动端开发式进行调试,快速排查移动端问题。 搭建步骤 1、安装依赖库。…...

别再使用[]来获取字典的值了,来尝试一下这些方法
字典 在Python中,字典(Dictionary)是一种非常灵活的数据结构,用于存储键值对(key-value pairs)。每个键都是唯一的,并且与某个值相关联。字典是Python中处理映射关系(即一个键对应一…...
如果你不愿意冒一切风险,就不要成为创业者:如何建立一个年收入 1800 万美元的支付业务
作者:Austin Mac Nab,VizyPay 的 CEO 兼创始人 在创业初期,如果有人告诉我,我需要冒一切风险才能成功,我大概会吓得绕道而行。但事实是,如果你不愿意冒一切风险,就不要成为创业者。本着这个信念…...

4.浮点数二分【求数的平方根】
模板 public class BinarySearch {// 检查x是否满足某种性质public static boolean check(double x) {// 实现具体的检查逻辑return false; // 这里仅为示例,实际根据需求修改}public static double bsearch_3(double l, double r) {final double eps 1e-6; // …...
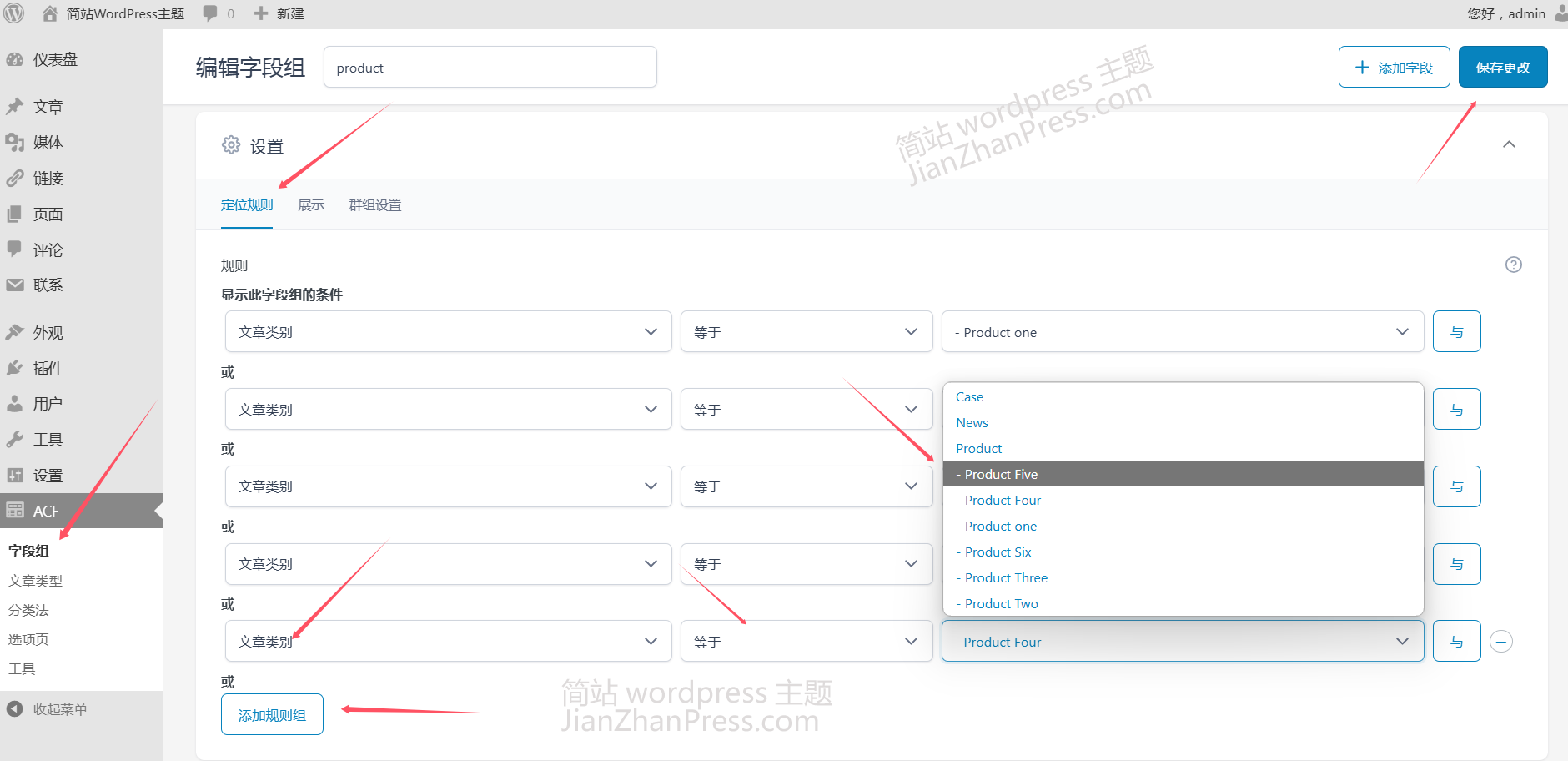
简站wordpress主题产品多图ACF插件设置方法
此教程仅适用于演示站有产品多图的主题,演示站没有产品多图的主题,就别往下看了,省得浪费时间。 1、给产品添加轮播图 简站wordpress主题有多个产品图的主题,添加产品轮播图的具体方法如下: 1.2、选择产品分类 添加…...

USB设备在Linux系统中的识别和加载过程
文章目录 一、USB设备的插入与检测二、中断处理与设备识别三、驱动程序加载与设备注册四、设备节点创建与权限分配五、设备初始化与通信 在Linux系统中,USB设备的自动识别和加载过程是一个高效且复杂的机制,确保了用户能够无缝地使用这些设备。本文将深入…...

nacos通过@Value动态刷新配置
Value获取最新值 引入jar包: <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-nacos-config</artifactId><version>2.2.1.RELEASE</version> </dependency>引入配置…...

[研发工具箱] 系列3.机电类常用的分类网站
工具箱系列1里,我们对国家标准馆提供的服务做了一些简介,在研发工作中还有一些非常宝贵的资讯来源,现在尽可能多的列举出一些宝贝网站: 1.文献标准类网站: 我经常会用到3 NTSL国家科技图书文献中心 之前提到的国家标…...
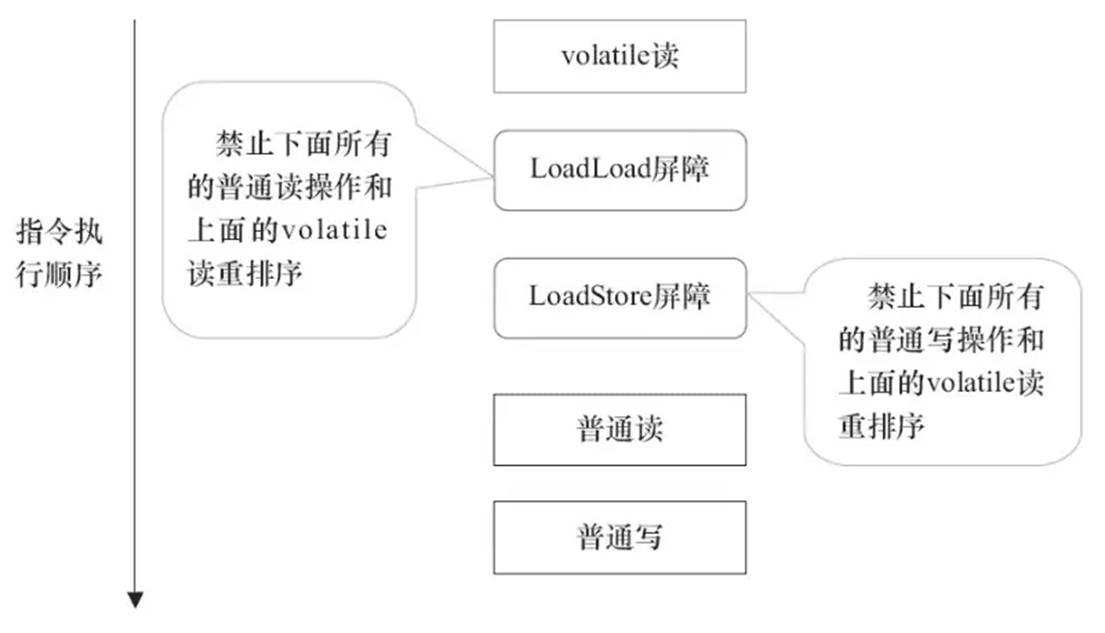
volatile关键字最全原理剖析
介绍 volatile是轻量级的同步机制,volatile可以用来解决可见性和有序性问题,但不保证原子性。 volatile的作用: 保证了不同线程对共享变量进行操作时的可见性,即一个线程修改了某个变量的值,这新值对其他线程来说是…...
)
mysql学习教程,从入门到精通,SQL RIGHT JOIN语句(24)
1、SQL RIGHT JOIN语句 RIGHT JOIN(也被称为RIGHT OUTER JOIN)是一种SQL语句,它用于从两个或多个表中根据连接条件返回右表(RIGHT JOIN语句中指定的表)的所有记录,以及左表中匹配的记录。如果左表中的行在…...

LeaferJS 动画、状态、过渡、游戏框架
LeaferJS 现阶段依然专注于绘图、交互和图形编辑场景。我们引入游戏场景,只是希望让 LeaferJS 被更多有需要的人看到,以充分发挥它的价值 LeaferJS 为你带来了全新的游戏、动画、状态和过渡功能,助你实现那些年少时的游戏梦想。我们引入了丰富…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
