LeetCode题练习与总结:为运算表达式设计优先级--241
一、题目描述
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 10^4 。
示例 1:
输入:expression = "2-1-1" 输出:[0,2] 解释: ((2-1)-1) = 0 (2-(1-1)) = 2
示例 2:
输入:expression = "2*3-4*5" 输出:[-34,-14,-10,-10,10] 解释: (2*(3-(4*5))) = -34 ((2*3)-(4*5)) = -14 ((2*(3-4))*5) = -10 (2*((3-4)*5)) = -10 (((2*3)-4)*5) = 10
提示:
1 <= expression.length <= 20expression由数字和算符'+'、'-'和'*'组成。- 输入表达式中的所有整数值在范围
[0, 99] - 输入表达式中的所有整数都没有前导
'-'或'+'表示符号。
二、解题思路
- 遍历给定的表达式字符串,找到所有的运算符。
- 对于每个运算符,可以将表达式分割成两部分:运算符左边的部分和右边的部分。
- 递归地对左边的部分和右边的部分分别求解,即计算它们的所有可能结果。
- 对于左边部分的所有可能结果和右边部分的所有可能结果,使用当前的运算符将它们组合起来,得到当前运算符位置的所有可能结果。
- 将所有运算符位置的所有可能结果合并起来,就是最终的结果。
三、具体代码
import java.util.ArrayList;
import java.util.List;class Solution {public List<Integer> diffWaysToCompute(String expression) {List<Integer> result = new ArrayList<>();// 遍历表达式字符串,寻找运算符for (int i = 0; i < expression.length(); i++) {char c = expression.charAt(i);// 如果当前字符是运算符if (c == '+' || c == '-' || c == '*') {// 分别计算运算符左右两边的所有可能结果List<Integer> left = diffWaysToCompute(expression.substring(0, i));List<Integer> right = diffWaysToCompute(expression.substring(i + 1));// 将左边和右边的所有可能结果组合起来for (int l : left) {for (int r : right) {if (c == '+') {result.add(l + r);} else if (c == '-') {result.add(l - r);} else if (c == '*') {result.add(l * r);}}}}}// 如果result为空,说明expression中没有运算符,即为一个数字if (result.isEmpty()) {result.add(Integer.parseInt(expression));}return result;}
}
这个实现通过递归方法,将问题分解成更小的子问题,并最终合并结果。在每次递归中,都会处理一个运算符,并计算其左右两边表达式的所有可能结果,然后将这些结果组合起来。如果递归到达表达式的末尾,说明没有更多的运算符,这时将字符串转换为整数并添加到结果列表中。
四、时间复杂度和空间复杂度
1. 时间复杂度
对于给定的字符串 expression,我们可以通过以下步骤来分析时间复杂度:
-
每次递归,我们都会遍历表达式字符串,寻找运算符。这个操作的时间复杂度是 O(n),其中 n 是字符串的长度。
-
对于每个运算符,我们将表达式分割成两部分,并递归地计算这两部分的所有可能结果。这意味着对于每个运算符,我们需要计算两个子问题的解。
-
假设
expression的长度为 n,那么最坏的情况下,每次递归都会产生两个长度为 n/2 的子问题(假设每次分割都是均匀的),直到子问题的大小减少到 1。
由于递归树是满二叉树,且每层需要 O(n) 的时间来处理,总的时间复杂度是 O(n * 2^n),其中 n 是字符串的长度,2^n 是递归树的高度。
2. 空间复杂度
空间复杂度主要取决于递归栈的深度以及存储结果的列表:
-
递归栈的深度与递归树的高度相同,最坏情况下是 O(2^n),其中 n 是字符串的长度。
-
每个递归调用中,我们都会创建两个列表来存储子问题的解,这些列表的大小在最坏情况下是 O(2^(n/2)),因为每个子问题可能产生一半大小的解集。
-
最终结果列表的大小是 O(2^n),因为可能存在 2^n 个不同的计算结果。
综上所述,空间复杂度主要由递归栈的深度和最终结果列表的大小决定,总的空间复杂度是 O(n * 2^n),其中 n 是字符串的长度。
五、总结知识点
-
类定义:
class关键字用于定义一个类。- 类名
Solution是自定义的,表示一个解决方案。
-
成员方法:
public关键字定义了方法的访问权限,表示该方法可以被外部访问。List<Integer>表示该方法返回一个整数列表。diffWaysToCompute是自定义的方法名,表示不同的计算方式。
-
数据结构:
List接口用于表示一个列表。ArrayList是List接口的一个实现,用于存储可动态调整大小的数组。
-
循环与条件判断:
for循环用于遍历字符串中的每个字符。if语句用于检查当前字符是否为运算符。char类型用于表示单个字符。
-
字符串操作:
substring方法用于获取字符串的子串。
-
递归:
diffWaysToCompute方法在内部调用自身,这是递归调用的一个例子。
-
异常处理:
Integer.parseInt方法用于将字符串转换为整数,这里没有显式异常处理,但假设输入总是有效的。
-
集合操作:
add方法用于向列表中添加元素。isEmpty方法用于检查列表是否为空。
-
逻辑与数学:
- 递归地将表达式分解为更小的部分,并组合结果,这是分治算法的一个应用。
- 根据不同的运算符执行相应的数学运算。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:为运算表达式设计优先级--241
一、题目描述 给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。 生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 10^…...

金融科技革命:API接口开放平台,畅通金融服务之路
金融科技是近年来蓬勃发展的领域,它利用先进的技术手段来改善和创新金融服务。在金融科技的革命中,API接口开放平台扮演着重要的角色,它通过提供统一的接口服务,让金融机构和其他行业能够更方便地进行数据交换和合作。本文将以挖数…...

Java8后新特性介绍
1.接口私有方法(Java9) 在Java9之前,interface接口只能定义abstract抽象方法和default默认方法。如果有多个默认方法使用了相同的处理逻辑,那只能写重复代码,或者再单独建个类进行调用。Java9解决了此类问题ÿ…...

Arthas monitor(方法执行监控)
文章目录 二、命令列表2.3 monitor/watch/trace/stack/tt 相关2.3.1 monitor(方法执行监控)举例1:监控demo.MathGame类,并且每5S更新一次状态。 二、命令列表 2.3 monitor/watch/trace/stack/tt 相关 使用场景: monit…...

语言的副作用
副作用产生于表达式中有至少一处计算,且其中全部或部分计算会影响表达式其他项,这可能产生副作用。编译器的优化很可能凸显副作用。 赋值 副作用并非都是有害的,比如基本的赋值 a b, 对a而言是产生副作用,但完成了赋值要求。 序…...

centos磁盘逻辑卷LVM创建
centos磁盘逻辑卷LVM创建 一、磁盘逻辑卷LVM说明二、centos磁盘使用情况三、LVM安装指南1.LVM工具安装1. yum list lvm2. yum search lvm3. yum search pvcreate4. yum list lvm25. yum install lvm2 2.创建物理卷2.1磁盘情况查看2.2创建物理卷(PV) 3.创…...

BUUCTF蜘蛛侠呀
解压后发现是流量包,好多icmp包 发现icmp包尾部有$$STRAT打头16进制的字符串,好多重复得。我们只需要提取尾部这些字符串是当icmp的type0时上图标识为褐色的字符串,还需要把16进制的字符串转为对应的字符串(bytes 类型)…...

大数据新视界 --大数据大厂之基于 MapReduce 的大数据并行计算实践
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

win自带录屏怎么用?让视频制作更简单!
win自带录屏怎么用?Windows系统内置的录屏功能,以其便捷高效著称,轻松满足多样化需求。无论是快速捕捉会议要点、制作教学视频,还是直播精彩游戏瞬间,都能一键启动,无缝录制。无需额外安装软件,…...

修改Kali Linux的镜像网站
由于官方的镜像可能会出现连接不上的问题导致无法安装我们所需要的包,所以需要切换镜像站为国内的,以下是一些国内常用的Kali Linux镜像网站,它们提供了与Kali Linux官方网站相同的软件包和资源,但访问速度更快: 清华…...
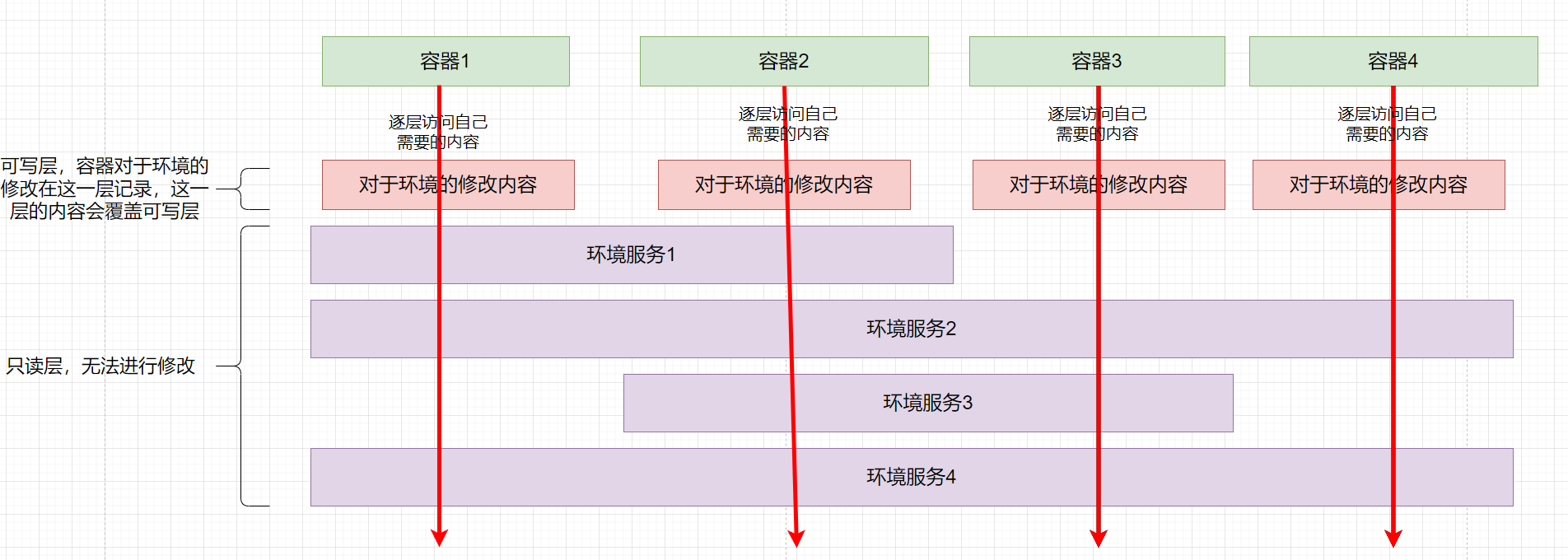
Docker精讲:基本安装,简单命令及核心概念
docker服务部署 docker是一个容器管理工具,其内部容器才是具体服务,所以我们在安装docker时不需要有太多定制内容,只需要通过yum安装即可 1. 更新系统包 #更新现有依赖包,防止现有依赖包版本过低影响docker安装 yum update2. 安…...

利用git将项目上传到github
采用git而不是在pycharm中共享的原因:可能会出现上图报错 目录 1、创建github仓库2、在 git bash 中初始化Git仓库,添加文件,上传代码 1、创建github仓库 2、在 git bash 中初始化Git仓库,添加文件,上传代码...

828华为云征文 | 华为云X实例CPU性能测试详解与优化策略
目录 引言 1. 测试环境搭建 1.1 测试实例的选择 1.2 CPU性能测试工具介绍 1.3 安装和配置Sysbench 2. CPU性能测试方法 2.1 测试场景设定 2.2 Sysbench单线程CPU性能测试 2.3 Sysbench多线程CPU性能测试(4线程) 2.4 高强度多线程CPU性能测试&a…...

ass字幕文件怎么导入视频mp4?ass字幕怎么编辑?视频加字幕超简单!
ass字幕文件怎么导入视频mp4?ass字幕怎么编辑?在视频制作和观看过程中,添加字幕是一项常见的需求,特别是对于外语视频或需要辅助阅读的场景。ASS(Advanced SubStation Alpha)字幕文件是一种常用的字幕格式&…...

camunda + oracle 启动报错 解决方法
启动报错如下: java.sql.SQLException: sql injection violation, comment not allow : select * from ( select a.*, ROWNUM rnum from (select RES.ID_,RES.REV_,RES.DUEDATE_,RES.PROCESS_INSTANCE_ID_,RES.EXCLUSIVE_from ACT_RU_JOB RESwhere (RES.RETRIES_ &g…...

变幅液压系统比例阀放大器
变幅液压系统是用于控制起重机或类似设备臂架角度变化的关键系统,它通过调节液压缸的伸缩来实现臂架的升降和变幅。以下是一些关于变幅液压系统的基本原理、组成和应用领域的信息: 基本原理:变幅液压系统通常由液压泵、液压缸、液压马达、控制…...

在 Ubuntu 安装 Python3.7(没有弯路)
注:当前Ubuntu版本为18.04 下载Python源码包 wget https://www.python.org/ftp/python/3.7.12/Python-3.7.12.tgz安装前准备 安装依赖组件 apt-get updateapt-get install build-essential zlib1g-dev libncurses5-dev libgdbm-dev libnss3-dev libssl-dev libs…...

Linux 简易shell编写
shell shell是壳,外壳的意思,一般我们使用linux系统有用图形化界面的也有使用命令行界面的,这两个都是一种shell,以命令行为例: 如图这个就是我这里的命令行格式,在$符后面写的就是执行的指令,…...

POLYGON Nature - Low Poly 3D Art by Synty 树木植物
一个低多边形资源包,包含可以添加到现有多边形风格游戏中的树木、植物、地形、岩石、道具和特效 FX 资源。 为 POLYGON 系列提供混合样式树这一新增功能。弥合 POLYGON 与更传统的层级资源之间的差距。还提供了一组经典的 POLYGON 风格的树木和植被以满足你的需求。 该包还附带…...

了解什么是瞪羚企业
瞪羚企业”是指以科技创新或商业模式创新为支撑,进入高成长期的中小企业。识别范围主要是符合国家和省战略性新兴产业发展方向的产业领域,涵盖新兴产业、新一代信息技术(包括大数据、物联网和云计算、高端软件、互联网)、生物健康…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
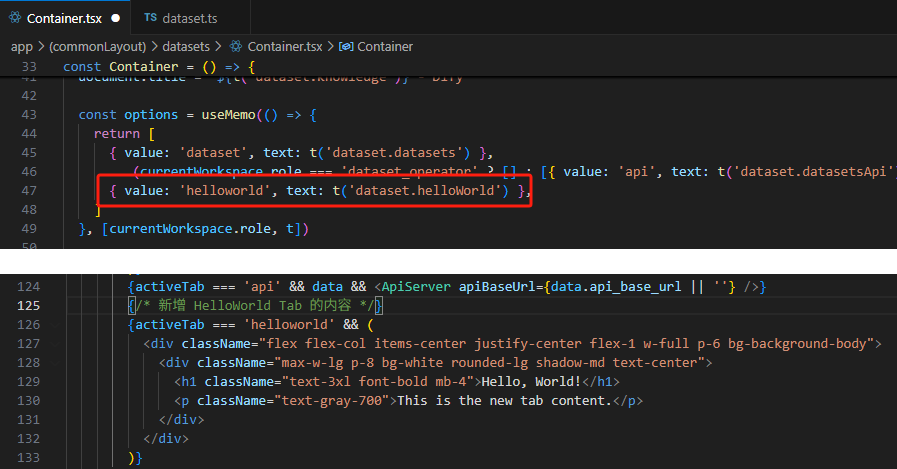
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
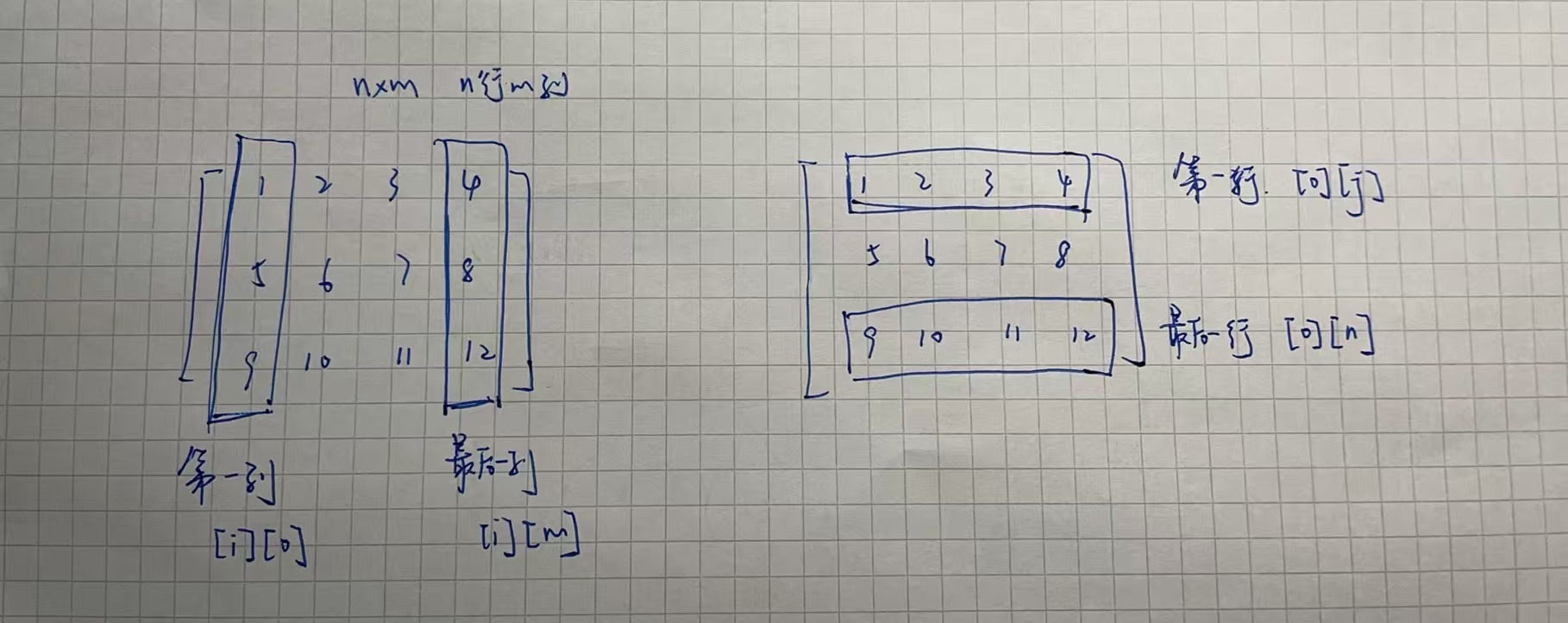
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...

PostgreSQL 对 IPv6 的支持情况
PostgreSQL 对 IPv6 的支持情况 PostgreSQL 全面支持 IPv6 网络协议,包括连接、存储和操作 IPv6 地址。以下是详细说明: 一、网络连接支持 1. 监听 IPv6 连接 在 postgresql.conf 中配置: listen_addresses 0.0.0.0,:: # 监听所有IPv4…...
