KKT实际运用 -MATLAB
- FMINCON函数可以很方便的求出:
fun:目标函数,即需要最小化的函数,输入参数为向量x,输出为标量f(x)。x0:初始点,即求解过程的起始点,可以是标量、向量或矩阵。A和b:线性不等式约束的系数矩阵和向量,满足A*x <= b。Aeq和beq:线性等式约束的系数矩阵和向量,满足Aeq*x = beq。lb和ub:变量的下界和上界向量,满足lb <= x <= ub。nonlcon:非线性约束函数(可选),定义非线性不等式c(x) <= 0和非线性等式ceq(x) = 0。options:优化选项(可选),用于控制求解过程的参数,如算法选择、容差设置等。
% 项目名称:KKT实际运用
% 更新时间:2024/09/25
% 背景:(Karush-Kuhn-Tucker方法)是一种用于求解约束优化问题的数学方法,该方法的核心思想是通过引入拉格朗日乘子和对偶性理论,将约束优化问题转化为无约束优化问题,从而简化求解过程。
% 作者:月白风清江有声 % 定义目标函数
fun = @(x) 4*x(1) - 3*x(2); % 假设我们要最小化的目标函数 % 初始点
x0 = [0, 0]; % 线性不等式约束 A*x <= b
A = [1, 1; 0, -1];
b = [4; 7]; % 线性等式约束(这里没有,所以留空)
Aeq = [];
beq = []; % 定义非线性不等式约束函数
% 注意:这个函数返回的是非线性不等式的原始表达式值,但fmincon会尝试最小化它
% 对于 -(x1-3)^2 + x2 + 1 >= 0,我们直接返回其表达式值
% 因为fmincon会尝试找到使这些值尽可能小的x,从而满足原不等式
% 定义非线性不等式约束函数
% 直接返回不等式约束的表达式值和空向量
%deal 函数用于同时返回两个值。第一个值是原不等式约束的表达式值,第二个值是一个空向量 [],表示没有非线性等式约束。
nonlincon = @(x) deal((x(1)-3)^2 - x(2) - 1, []);
% 调用fmincon
options = optimoptions('fmincon','Algorithm','sqp'); % 设置算法为SQP
[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, [], [], nonlincon, options);
% 显示结果
disp('最优解 x:');
disp(x);
disp('目标函数值 fval:');
disp(fval);% 第二个优化问题 % 定义目标函数(注意这里使用了三个变量)
fun_bar = @(x_bar) -3*x_bar(1)^2 - x_bar(2)^2 - 2*x_bar(3)^2; % 初始点(现在是三维的)
x0_bar = [1, 1, 1]; % 线性不等式约束 A_bar*x_bar <= b_bar A_bar = [1, -1, 0; -1, 0, 0; 0, -1, 0; 0, 0, -1];
b_bar = [0; 0; 0; 0]; Aeq_bar = [];
beq_bar = []; nonlincon_bar = @(x_bar) deal([], (x_bar(1)^2 + x_bar(2))^2 + x_bar(3)^2 - 3);
% 调用fmincon
options_bar = optimoptions('fmincon','Algorithm','sqp'); % 设置算法为SQP
[x_bar, fval_bar] = fmincon(fun_bar, x0_bar, A_bar, b_bar, Aeq_bar, beq_bar, [], [], nonlincon_bar, options_bar); % 显示结果
disp('第二个优化问题的最优解 x_bar:');
disp(x_bar);
disp('第二个优化问题的目标函数值 fval_bar:');
disp(fval_bar);
相关文章:

KKT实际运用 -MATLAB
FMINCON函数可以很方便的求出:fun:目标函数,即需要最小化的函数,输入参数为向量x,输出为标量f(x)。x0:初始点,即求解过程的起始点,可以是标量、向量或矩阵。A和b:线性不等…...

php在线相册
1、将静态页面效果完成 解压到www里 整个数据 暂时是错误的 建立连接密码为root 运行sql文件 右键根目录刷新 刷新后成功 开始 测试 如果需要上传照片,点击创建相册,选择上传文件,选择文件后退出 导入alumbenew2 2.提交表单方式 3.利用ph…...

Xcode手动安装SDK模拟器
1.下载SDK模拟器&Xcode SDK和Xcode官方下载地址 2.下载好后使用命令将SDK导入到Xcode中如下命令 注:我是在/Applications 目录下执行的命令,模拟其地址直接拖拽过来 sudo xcode-select -s Xcode.app xcodebuild -runFirstLaunch xcodebuild -imp…...
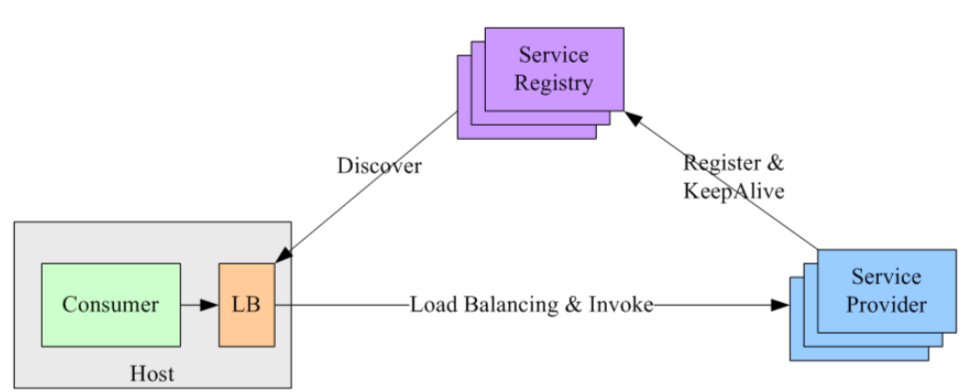
Docker安装consul + go使用consul + consul知识
1. 什么是服务注册和发现 假如这个产品已经在线上运行,有一天运营想搞一场促销活动,那么我们相对应的【用户服务】可能就要新开启三个微服务实例来支撑这场促销活动。而与此同时,作为苦逼程序员的你就只有手动去 API gateway 中添加新增的这…...

JWT 漏洞 - 学习手册
0x01:JWT 前导知识 0x0101:JWT 详解 0x02:JWT 漏洞介绍 0x0201:JWT 漏洞介绍 0x03:JWT 挖掘思路 JWT 漏洞挖掘思路 - JWT Payload 敏感信息泄露 备注:通过泄露的 JWT Payload 获取用户的敏感信息&#…...

HTML【知识改变命运】03font 字体标签
题目:在页面上显示"北京"两个字,字体为微软雅黑,颜色为红色,大小为40xp; font标签可以修饰字体的大小,颜色,和字体 属性:color颜色,face字体,size大…...

集师专属知识付费小程序搭建 心理咨询小程序搭建
一、产品简介 集师SaaS知识付费软件,为知识创业者或商家提供一站式内容交付解决方案,助力商家搭建集品牌传播、商业变现和用户运营于一体的线上知识服务系统,覆盖全渠道经营场景,占据每个流量入口,使流量变现快速高效…...

https://www.aitoolpath.com/ 一个工具数据库,目前储存了有2000+各种工具。每日更新
AI 工具爆炸?别怕,这个网站帮你整理好了! 哇塞,兄弟们!AI 时代真的来了!现在各种 AI 工具跟雨后春笋似的,噌噌噌地往外冒。AI 写作、AI 绘画、AI 代码生成……简直是要逆天啊! 可是…...
)
科技的成就(六十三)
583、八小时工作制 最先提出这种理念的人竟然也是一名企业家,而且还是一名空想社会主义者。这名叫做罗伯特欧文的英国人,也凭借先进的人本管理理念成为了现代人事管理之父。 584、SDN(软件定义网络) "SDN(软件定…...

浅谈抗量子密码学:保护未来的数字安全
一、引言 随着量子计算机技术的发展,传统的加密算法面临前所未有的挑战。量子计算机利用量子位(qubits)的特性,能够在理论上比经典计算机更快地破解现有的加密系统。为了应对这一威胁,研究者们正在开发所谓的“抗量子…...

10款物联网开源嵌入式操作系统对比分析
摘要 本文对目前市场上广受欢迎的10款物联网开源嵌入式操作系统进行了深度对比分析,包括Huawei LiteOS、RT-Thread、AliOS Things等。通过探讨这些操作系统的实时性、可扩展性、特点、运行要求、开发社区活跃度和应用领域等方面,帮助开发者更好地理解它…...

Elasticsearch深度攻略:核心概念与实践应用
目录 一、Elasticsearch简介1、Elasticsearch是什么2、Elasticsearch的应用场景3、Elasticsearch的核心概念 二、Elasticsearch安装与配置1、安装Elasticsearch(1)系统要求(2)下载Elasticsearch(3)解压安装…...

TLS详解
什么是TLS TLS(Transport Layer Security)传输层安全性协议 ,它的前身是SSL(Secure Sockets Layer)安全套接层,是一个被应用程序用来在网络中安全的通讯协议, 防止电子邮件、网页、消息以及其他协议被篡改或是窃听。是用来替代SSL的…...

正则表达式中的特殊字符
正则表达式中的特殊字符 字符类预定义字符类量词锚点分组和捕获选择、分支和条件反义和否定转义字符示例 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神的孩子都在歌唱 在正则表达式中,有许…...

EP42 公告详情页
文件路径: E:/homework/uniappv3tswallpaper/api/apis.js 先添加相应的api。 import {request } from "/utils/requset.js"export function apiGetBanner() {return request({url: "/homeBanner"}) } export function apiGetDayRandom() {ret…...

游戏找不到xinput1_3.dll的原因及解决方法
1. xinput1_3.dll 基本信息 1.1 文件名 xinput1_3.dll 是一个动态链接库(DLL)文件,它属于 Microsoft DirectX for Windows 的一部分。这个文件主要负责处理与 Xbox 360 控制器和其他兼容 XInput 标准的游戏手柄相关的输入信号,确…...

防反接电路设计
方案1 串联二极管, 优点:成本低、设计简单 缺点:损耗大,P ui 方案2 串联自恢复保险丝 当电源反接的时候,D4导通,F2超过跳闸带你留,就会断开,从而保护了后级电路 方案3 H桥电路…...

SpringMVC源码-AbstractHandlerMethodMapping处理器映射器将@Controller修饰类方法存储到处理器映射器
SpringMVC九大内置组件之HandlerMapping处理器映射器-AbstractHandlerMethodMapping类以及子类RequestMappingHandlerMapping如何将Controller修饰的注解类以及类下被注解RequestMapping修饰的方法存储到处理器映射器中。 从RequestMappingHandlerMapping寻找: AbstractHandle…...

毕业设计选题:基于ssm+vue+uniapp的购物系统小程序
开发语言:Java框架:ssmuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:M…...
】力扣583. 两个字符串的删除操作)
【动态规划-最长公共子序列(LCS)】力扣583. 两个字符串的删除操作
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 “sea”, word2 “eat” 输出: 2 解释: 第一步将 “sea” 变为 “ea” ,第二步将 "e…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
