iSTFT 完美重构的条件详解
目录
- 引言
- 1. 短时傅里叶变换(STFT)与逆变换(iSTFT)概述
- 2. 完美重构的条件
- 3. 数学推导
- 4. 实现要点
- 5. 示例代码
- 6. 总结
引言
在数字信号处理领域,短时傅里叶变换(Short-Time Fourier Transform,简称 STFT)及其逆变换(Inverse Short-Time Fourier Transform,简称 iSTFT)是分析和处理非平稳信号的强大工具。STFT 通过将信号分割成短时帧,并对每一帧进行傅里叶变换,从而在时间-频率域中表示信号。iSTFT 则用于将频域信息重构回时域信号。
实现 iSTFT 的完美重构,即从 STFT 结果中无失真地恢复原始信号,是许多应用(如语音处理、音频编码、音乐信号处理等)的关键。本文将详细探讨 iSTFT 完美重构的条件,涵盖理论基础、数学表达及实际实现要点。
1. 短时傅里叶变换(STFT)与逆变换(iSTFT)概述
1.1 短时傅里叶变换(STFT)
STFT 是将信号 x(t) 通过一个滑动窗口函数 w(t) 分割成多个重叠的短时帧,然后对每一帧进行傅里叶变换,得到信号在时间-频率域中的表示:

1.2 逆短时傅里叶变换(iSTFT)
iSTFT 的目标是从 STFT 的频域表示 X(m,k) 重构时域信号 x(n)。重构过程涉及以下步骤:
对每个频域帧进行逆傅里叶变换,得到时域的短时帧。
将所有短时帧按照跳步 H 重叠并相加,形成最终的重构信号。
2. 完美重构的条件
实现 iSTFT 的完美重构,需满足以下主要条件:
2.1 窗口函数的重叠相加(Overlap-Add)性质
窗口函数 w(t) 必须满足 常数重叠相加(Constant Overlap-Add,COLA) 条件,即在任意时间点上,所有重叠窗口的和为常数。这一条件确保在重叠相加过程中,不会引入失真或幅度变化。
数学表达为:

2.1.1 窗口函数选择
满足 COLA 条件的常用窗口函数包括:
汉明窗(Hamming Window)
汉宁窗(Hann Window)
高斯窗(Gaussian Window)
特别是 汉宁窗 是最常用的选择,因为它自然满足 COLA 条件,当跳步 H 选择为窗口长度的一半时(即 50% 重叠),能够实现完美重构。
2.2 跳步大小(Hop Size)与窗口长度的关系
跳步 H 与窗口长度 L 必须满足特定的比例关系,通常根据窗口函数的重叠特性确定。常见的关系包括:
50% 重叠:H=L/2
25% 重叠:H=L/4
75% 重叠:H=3L/4对于汉宁窗,当 H=L/2 时,满足 COLA 条件,确保完美重构。
2.3 窗口函数的正交性
某些情况下,窗口函数需要满足正交性,即不同窗口在频域上的重叠最小,以减少失真和混叠现象。这对于完美重构也是必要的,尤其在频域分析和处理时。
2.4 频域补偿
在某些实现中,需要在频域对窗口函数进行补偿,以确保在重构过程中幅度的一致性。这通常涉及归一化窗口函数,确保重叠相加后的总增益为1。
3. 数学推导
为了更深入理解完美重构的条件,我们通过数学推导来说明。
3.1 STFT 与 iSTFT 的关系
设信号 x(n) 的 STFT 为 X(m,k),iSTFT 的重构过程为:


3.3 正交窗口与完美重构
当窗口函数满足正交性时,即不同窗口之间的内积为零,可以进一步确保在频域上的独立性,减少混叠和失真,从而实现完美重构。
4. 实现要点
在实际应用中,实现 iSTFT 完美重构需要注意以下几点:
4.1 窗口函数的选择与设计
选择满足 COLA 条件的窗口函数,并根据需要调整跳步大小
𝐻
H。汉宁窗是常用选择,但在特定应用中,可能需要设计自定义窗口函数以满足特定条件。
4.2 窗口归一化
在重构过程中,确保窗口函数的重叠相加为1。这通常通过选择合适的窗口函数和跳步大小实现,或者在重叠相加后进行归一化处理。
4.3 跳步大小与计算效率
选择合适的跳步大小不仅影响重构质量,还影响计算效率。较小的跳步大小(高重叠)通常提高重构质量,但增加计算负担。需要在质量与效率之间找到平衡。
4.4 边界处理
处理信号的起始和结束部分,避免边界效应对重构质量的影响。常用方法包括在信号两端进行零填充或镜像填充。
5. 示例代码
以下是一个基于 C++ 的简单 iSTFT 实现示例,展示了如何满足完美重构的条件。为了简化,假设使用汉宁窗且跳步为窗口长度的一半。
#include <iostream>
#include <vector>
#include <cmath>// 定义 PI 常量
const double PI = 3.14159265358979323846;// 生成汉宁窗
std::vector<double> hanning_window(int N) {std::vector<double> window(N);for(int n = 0; n < N; ++n) {window[n] = 0.5 * (1 - cos(2 * PI * n / (N - 1)));}return window;
}// 简单的 iSTFT 实现
std::vector<double> istft(const std::vector<std::vector<std::complex<double>>>& stft_matrix, int N, int H) {int num_frames = stft_matrix.size();int signal_length = H * (num_frames -1) + N;std::vector<double> signal(signal_length, 0.0);std::vector<double> window = hanning_window(N);for(int m = 0; m < num_frames; ++m) {// 逆傅里叶变换(这里只做简单处理,实际应使用IFFT)std::vector<double> frame_time_domain(N, 0.0);for(int k = 0; k < N; ++k) {frame_time_domain[k] = std::abs(stft_matrix[m][k]);}// 加窗并重叠相加for(int n = 0; n < N; ++n) {signal[m * H + n] += frame_time_domain[n] * window[n];}}return signal;
}int main() {// 示例:创建简单的 STFT 矩阵(实际应由 STFT 生成)int N = 4; // 窗口长度int H = 2; // 跳步大小std::vector<std::vector<std::complex<double>>> stft_matrix = {{ {1,0}, {2,0}, {3,0}, {4,0} },{ {5,0}, {6,0}, {7,0}, {8,0} },{ {9,0}, {10,0}, {11,0}, {12,0} }};// 执行 iSTFTstd::vector<double> reconstructed_signal = istft(stft_matrix, N, H);// 输出重构信号std::cout << "Reconstructed Signal:" << std::endl;for(auto sample : reconstructed_signal) {std::cout << sample << " ";}std::cout << std::endl;return 0;
}
注意:上述代码为简化示例,实际应用中需要使用逆傅里叶变换(如 IFFT)处理 STFT 矩阵,并处理复数运算。确保窗口函数和跳步大小满足 COLA 条件是实现完美重构的关键。
6. 总结
实现 iSTFT 的完美重构需要满足多个条件,主要包括:
窗口函数满足重叠相加(COLA)条件:选择适当的窗口函数(如汉宁窗)并调整跳步大小 H,确保窗口的重叠部分在重叠相加后为常数。
跳步大小与窗口长度的合理关系:通常选择跳步为窗口长度的一半,以实现 50% 重叠,满足 COLA 条件。
窗口函数的正交性:确保窗口函数在频域上的正交性,减少失真和混叠。
频域补偿与归一化:在频域对窗口函数进行补偿,确保重叠相加后的总增益为1,避免幅度失真。
通过满足上述条件,可以在实际应用中实现 iSTFT 的完美重构,从而在时间-频率域中有效地分析和处理信号。
相关文章:

iSTFT 完美重构的条件详解
目录 引言1. 短时傅里叶变换(STFT)与逆变换(iSTFT)概述2. 完美重构的条件3. 数学推导4. 实现要点5. 示例代码6. 总结 引言 在数字信号处理领域,短时傅里叶变换(Short-Time Fourier Transform,简…...
可以基于多种加密算法)
SSH(安全外壳协议)可以基于多种加密算法
SSH(安全外壳协议)可以基于多种加密算法,确保数据的机密性和完整性。以下是 SSH 中常见的加密类型: 1. 对称加密 对称加密算法用于加密会话中的数据,常见的算法包括: AES(高级加密标准&#…...

Navicat 工具 下载安装
准备工作 下载 下载链接:https://www.123865.com/ps/EF7OTd-kdAnH 演示环境 操作系统:windows10 产品:Navicat 版本: 15.0.25 注意:如果需要其他版本可以自行下载。 安装步骤 1、解压(如果解压中出现提示…...

家用高清投影仪怎么选?目前口碑最好的投影仪推荐
双十一马上要到了,而且今年还有投影仪的家电国补,所以大家入手投影仪的需求也越来越多,但是家用高清投影仪怎么选?什么投影仪最适合家用?家庭投影仪哪个牌子质量最好?今天就给大家做一个2024性价比高的家用…...

阿里云盾同步漏洞之限制请求数
阿里云sdk不支持一次性请求太多,所以我们需要限制每次请求最大1000条,此代码无任何参考意义。仅做记录 func VulList(hole_type string) ([]*sas20181203.DescribeVulListResponseBodyVulRecords, error) {pageSize : 20allItems : make([]*sas20181203…...

docker安装kafka-manager
kafkamanager docker安装_mob64ca12d80f3a的技术博客_51CTO博客 # 1、拉取镜像及创建容器 docker pull hlebalbau/kafka-manager docker run -d --name kafka-manager -p 9000:9000 --networkhost hlebalbau/kafka-manager# 2、增设端口 腾讯云# 3、修改防火墙 sudo firewall-…...

Android Studio 新版本 Logcat 的使用详解
点击进入官方Logcat介绍 一个好的Android程序员要会使用AndroidStudio自带的Logcat查看日志,会Log定位也是查找程序bug的第一关键。同时Logcat是一个查看和处理日志消息的工具,它可以更快的帮助开发者调试应用程序。 步入正题,看图说话。 点…...

基于php摄影门户网站
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码 精品专栏:Java精选实战项目…...

uniapp中uni.request的统一封装 (ts版)
文章目录 前言一、我们为什么要去封装?二、具体实现1.创建一个请求封装文件:2.封装 uni.request:3.如何去使用? 总结 前言 在uniapp中如何去更简洁高效的发送我们的请求,下面就介绍了uni.request()二次封装。 一、我们…...
)
记录一次gRpc流式操作(jedis版)
使用背景: 从redis队列中发送和消费消息.(使用gRpc的流式实现的消费消息) gRpc协议类定义 service方法定义 service MQDataService{ rpc sendFacebookAndroidMsg(google.protobuf.StringValue)returns (ResultProto); rpc receiveFacebookAndroidMsg(empty)returns (stream g…...

20241001国庆学习
n60f/p 这个n是指旋转磁场的速度。 极数表示旋转转子的永磁体极数,具有一对N极/S极的电机称为双极电机。 极数可以是2、4、6、8等。 (从电机控制的角度来看,当极数增加一倍时,转速将减半,当极数增加四倍时…...
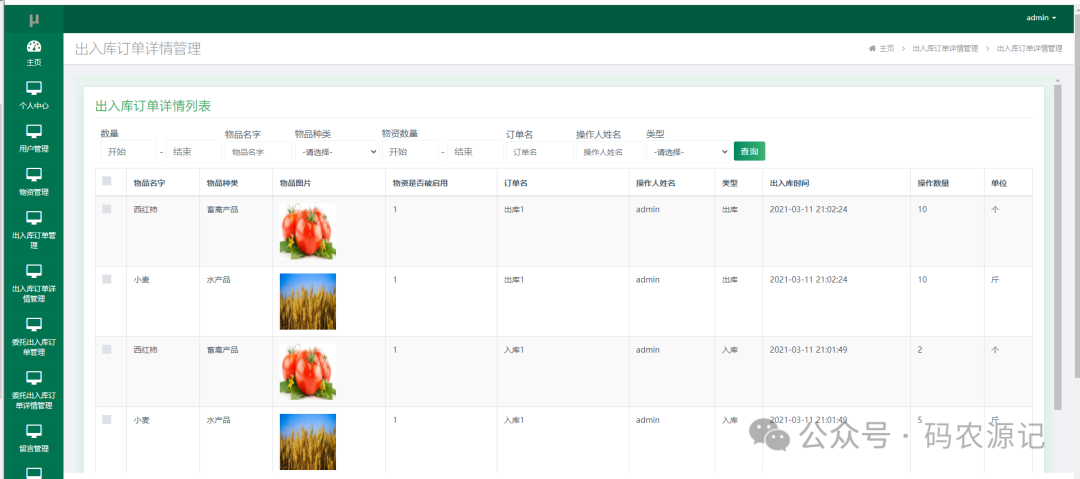
基于SSM的农产品仓库管理系统【附源码】
基于SSM的农产品仓库管理系统(源码L文说明文档) 目录 4 系统设计 4.1 系统概要设计 4.2 系统功能结构设计 4.3 数据库设计 4.3.1 数据库E-R图设计 4.3.2 数据库表结构设计 5 系统实现 5.1 管理员功能介绍 5.1.1 用户管…...

fmt:C++ 格式化库
fmt 是一个现代化、快速且安全的 C 格式化库,专注于高效地格式化文本。它提供了类似 Python 的 format 功能,但具有更高的性能和类型安全特性。fmt 库在处理字符串格式化、日志输出以及构建用户友好的输出时尤为强大。自从 C20 标准引入 std::format 后&…...

RabbitMQ MQ的可靠性及消费者的可靠性
1.MQ可靠性: 如何保证消息的可靠性: (1).通过配置可以让交换机、队列、以及发送的消息都持久化。这样队列中的消息会持久化到磁盘,MQ重起消息依然存在。 (2).3.6.0版本开始,RabbitMQ引入了惰性队列模式,这种模式下&am…...

使用 Nexus 代理 Docker Hub 的配置指南
在本篇文章中,我们将详细介绍如何配置 Nexus 以代理 Docker Hub,从而实现更高效的镜像管理。以下步骤涵盖了从 Nexus 的安装到 Docker 客户端的配置。 1. 配置 Nexus 1.1 登录 Nexus 打开浏览器,访问 Nexus 的 URL(例如 http:/…...

笔记整理—linux进程部分(4)进程状态与守护进程
进程的几种重要状态,就绪态;运行态;僵尸态;等待态(浅度睡眠、深度睡眠);停止态。 就单核CPU而言,在同一时间只能运行一个进程,但实际上要运行的进程不止一个,…...
# VirtualBox中安装的CentOS 6.5网络设置为NAT模式时,怎么使用SecureCRT连接CentOS6.5系统?
VirtualBox中安装的CentOS 6.5网络设置为NAT模式时,怎么使用SecureCRT连接CentOS6.5系统? 一、查询 【VirtualBox Host-Only Network】虚拟网卡的网络配置 IP。 1、按键盘上WIN R 组合键,打开【运行】,输入【 ncpa.cpl 】&…...
)
7-1.Android SQLite 之 SQLiteDatabase 简单编码模板(SQLiteDatabase 使用、SQL 语句编写)
一、SQLiteDatabase SQLite 是一种轻量级的数据库引擎,它非常适合在移动设备(例如,Android)上使用 SQLiteDatabase 允许应用程序与 SQLite 数据库进行交互,它提供了增删改查等一系列方法 二、SQLiteDatabase 简单编码…...
求取算法)
灰度图像重心(质心)求取算法
1、图像的重心坐标计算 假设我们有一个二维图像,其中 (x, y) 表示图像中每个像素的坐标。I(x, y) 表示图像在 (x, y) 处的亮度(或像素值),通常是灰度值。 图像的重心坐标 (X, Y) 可以通过以下公式计算: X = Σ [x * I(x, y)] / Σ I(x, y) Y = Σ [y * I(x, y)] / Σ I(…...

k8s 1.28.2 集群部署 ingress 1.11.1 包含 admission-webhook
文章目录 [toc]证书创建部署 ingress-controlleringress 验证创建测试 nginx pod创建错误的 ingress 配置创建正确的 ingress 配置 ingress 官方 yaml 文件:deploy.yaml基于官方 yaml 文件做了一些修改 官方的 svc 是 ClusterIP 和 LoadBalancer,我这边把…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
