力扣题解1870
这道题是一个典型的算法题,涉及计算在限制的时间内列车速度的最小值。这是一个优化问题,通常需要使用二分查找来求解。
题目描述(中等)
准时到达的列车最小时速
给你一个浮点数 hour ,表示你到达办公室可用的总通勤时间。要到达办公室,你必须按给定次序乘坐 n 趟列车。另给你一个长度为 n 的整数数组 dist ,其中 dist[i] 表示第 i 趟列车的行驶距离(单位是千米)。
每趟列车均只能在整点发车,所以你可能需要在两趟列车之间等待一段时间。
例如,第 1 趟列车需要 1.5 小时,那你必须再等待 0.5 小时,搭乘在第 2 小时发车的第 2 趟列车。
返回能满足你准时到达办公室所要求全部列车的 最小正整数 时速(单位:千米每小时),如果无法准时到达,则返回 -1 。
生成的测试用例保证答案不超过 107 ,且 hour 的 小数点后最多存在两位数字 。

题目大意:
- 你需要乘坐 n 趟列车,并且需要按给定的顺序乘坐。
- 每趟列车都要在整点发车,所以可能需要在两趟列车之间等待。
- 你可以给定一个浮点数 hour,作为你所能使用的最大通勤时间。
- 需要找到一个最小的正整数速度,使得总用时不超过给定的 hour,无法达到则返回 -1。
解题思路:
- 理解等待时间:由于列车只能整点发车,即使乘车时间不满整数小时,也需要等到下一个整数小时。
- 计算用时:
- 对于前 n-1 趟列车,必须在整点发车。其总时间为这些列车每趟到达所需时间的上限。
- 最后一趟列车则直接计算实际用时,因为它不需要等下一个整点发车。
- 二分查找:
- 初始最小速度设为1,最大速度设定为题目保证的上限(或使用一个足够大的值)。
- 使用二分查找来找到使得总乘机时间不超过 hour 的最小整数速度。
- 对于每个速度,通过计算每趟列车旅游所消耗的时间来判断该速度是否符合条件。
C和C++代码实现:
C++代码
bool canReachOnTime(const vector<int>& dist, double hour, int speed) {double totalTime = 0.0;int n = dist.size();for (int i = 0; i < n; ++i) {double timeNeeded = static_cast<double>(dist[i]) / speed;if (i == n - 1) {totalTime += timeNeeded; // Last train, no need to round up} else {totalTime += ceil(timeNeeded); // Round up for all but the last train}}return totalTime <= hour;
}int minSpeedOnTime(const vector<int>& dist, double hour) {int left = 1, right = 1e7, minSpeed = -1;while (left <= right) {int mid = left + (right - left) / 2;if (canReachOnTime(dist, hour, mid)) {minSpeed = mid;right = mid - 1;} else {left = mid + 1;}}return minSpeed;
}C代码
由于C语言的math.h库并没有很好的支持浮点的ceil函数,你可能需要手动编写这个功能。
#include <stdio.h>
#include <math.h>int canReachOnTime(int* dist, int distSize, double hour, int speed) {double totalTime = 0.0;for (int i = 0; i < distSize; ++i) {double timeNeeded = (double)dist[i] / speed;if (i == distSize - 1) {totalTime += timeNeeded; // Last train, no need to round up} else {totalTime += ceil(timeNeeded); // Round up for all but the last train}}return totalTime <= hour;
}int minSpeedOnTime(int* dist, int distSize, double hour) {int left = 1, right = 10000000, minSpeed = -1;while (left <= right) {int mid = left + (right - left) / 2;if (canReachOnTime(dist, distSize, hour, mid)) {minSpeed = mid;right = mid - 1;} else {left = mid + 1;}}return minSpeed;
}int main() {int dist[] = {1, 3, 2};int n = sizeof(dist) / sizeof(dist[0]);double hour = 2.7;printf("Minimum speed required: %d\n", minSpeedOnTime(dist, n, hour));return 0;
}
算法和代码分析:
canReachOnTime函数:这个辅助函数判断给定的速度下能否在限制时间内到达。它遍历所有列车计算总用时。对倒数第二趟列车,使用ceil将乘车时间圆整至下一整数以模拟等待时间的影响。- 二分查找:利用二分查找来优化最小的速度搜索,将搜索空间从1到10000000,每次通过中值检验是否满足时间条件,不符合则增加速度范围,符合则记录并尝试更小速度。
- 复杂度:二分查找的复杂度为O(log M),其中M为速度的搜索范围,判断能否到达的复杂度为O(N),因此总复杂度为O(N log M)。
相关文章:

力扣题解1870
这道题是一个典型的算法题,涉及计算在限制的时间内列车速度的最小值。这是一个优化问题,通常需要使用二分查找来求解。 题目描述(中等) 准时到达的列车最小时速 给你一个浮点数 hour ,表示你到达办公室可用的总通勤时…...

D3.js数据可视化基础——基于Notepad++、IDEA前端开发
实验:D3.js数据可视化基础 1、实验名称 D3数据可视化基础 2、实验目的 熟悉D3数据可视化的使用方法。 3、实验原理 D3 的全称是(Data-Driven Documents),是一个被数据驱动的文档,其实就是一个 JavaScript 的函数库,使用它主要是用来做数据可视化的。本次实…...

在Robot Framework中Run Keyword If的用法
基本用法使用 ELSE使用 ELSE IF使用内置变量使用Python表达式本文永久更新地址: 在Robot Framework中,Run Keyword If 是一个条件执行的关键字,它允许根据某个条件来决定是否执行某个关键字。下面是 Run Keyword If 的基本用法: Run Keyword…...

虚拟机ip突然看不了了
打印大致如下: 解决办法 如果您发现虚拟机的IP地址与主机不在同一网段,可以采取的措施之一是调整网络设置。将虚拟机的网络模式更改为桥接模式,这样它就会获得与主机相同的IP地址,从而处于同一网段。或者,您可以使用…...

LeetCode[中等] 763. 划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。 返回一个表示每个字符串片段的长度的列表。 思路 贪心…...

Java LeetCode每日一题
997. 找到小镇的法官 package JavaExercise20241002;public class JavaExercise {public static void main(String[] args) {int[][] array {{1,3},{2,3},{3,1}};Solution solution new Solution();System.out.println(solution.findJudge(3, array));} }class Solution {pu…...

数据结构--集合框架
目录 1. 什么是集合框架 2. 背后所涉及的数据结构以及算法 2.1 什么是数据结构 2.2 容器背后对应的数据结构 1. 什么是集合框架 Java 集合框架 Java Collection Framework ,又被称为容器 container ,是定义在 java.util 包下的一组接口 int…...

Win10鼠标总是频繁自动失去焦点-非常有效-重启之后立竿见影
针对Win10鼠标频繁自动失去焦点的问题,可以尝试以下解决方案: 一、修改注册表(最有效的方法-重启之后立竿见影) 打开注册表编辑器: 按下WindowsR组合键,打开运行窗口。在运行窗口中输入“regedit”&#x…...

智能涌现|迎接智能时代,算力产业重构未来
前言 OpenAI首席执行官山姆奥特曼在《智能时代》中描绘了一个令人振奋的未来图景,其中算力产业将扮演至关重要的角色。奥特曼预测,我们可能在“几千天内”迎来超级智能,这一进程将极大加速社会结构的智能化转型。 这一预测与算力产业的未来…...

关于HTML 案例_个人简历展示01
案例效果展示 代码 <!DOCTYPE html> <lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>个人简历信息</title> </he…...

【前端开发入门】css快速入门
目录 引言一、css盒模型1. 盒模型概念2. 盒模型案例 二、css编写1. html文件内部编写1.1 标签style属性编写1.2 css选择器关联1.2.1 id选择器1.2.2 class选择器1.2.3 标签选择器1.2.4 css选择器作用域1.2.5 其他选择器1.2.6 各css选择器优先级 2. 单独维护css文件2.1 创建css文…...

java中创建不可变集合
一.应用场景 二.创建不可变集合的书写格式(List,Set,Map) List集合 package com.njau.d9_immutable;import java.util.Iterator; import java.util.List;/*** 创建不可变集合:List.of()方法* "张三","李四","王五…...
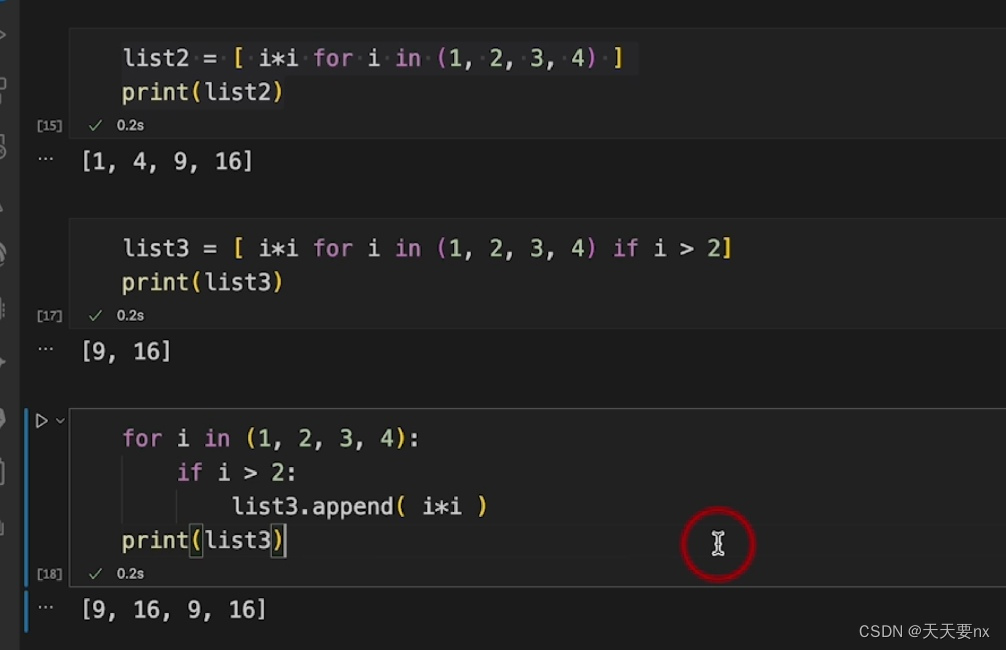
D25【 python 接口自动化学习】- python 基础之判断与循环
day25 for 循环 学习日期:20241002 学习目标:判断与循环﹣-35 for 循环:如何遍历一个对象里的所有元素? 学习笔记: for 循环与while循环的区别 for循环的定义 使用for循环遍历序列 使用for循环遍历字典…...

HTTP1.0和HTTP1.1有什么区别
HTTP/1.0 和 HTTP/1.1 是两个不同版本的 HTTP 协议。虽然它们的核心功能都是提供网页数据传输,但 HTTP/1.1 对 HTTP/1.0 做了很多改进,提升了性能和灵活性。以下是它们的主要区别: 1. 持久连接(Persistent Connection)…...

卡夫卡的理解
一、架构理解 在这个单聊新架构中,涉及多个服务器组件共同协作来实现单聊功能。 ChatAccessServer:可能负责处理单聊相关的访问请求,比如用户登录单聊以及发送单消息的请求接入。ChatHttpPushServer:推测其用于通过 HTTP 协议推…...

基础算法之滑动窗口--Java实现(上)--LeetCode题解:长度最小的子数组-无重复字符的子串-最大连续1的个数III-将x减到0的最小操作数
这里是Thembefue 今天讲解算法中较为经典的一个算法 > 滑动窗口 本讲解主要通过题目来讲解以理解算法 讲解分为三部分:题目解析 > 算法讲解 > 编写代码 滑动窗口 在正式进入题目的讲解之前,得先了解一下什么是滑动窗口,以及应该在什…...

Linux -- 文件系统(文件在磁盘中的存储)
目录 前言: 了解机械磁盘 初始盘片与磁头 盘片是怎么存数据的呢? 详解盘片 如何访问磁盘中的一个扇区呢? -- CHS 定位法 磁盘的逻辑存储 LBA(Logical Block Addressing --- 逻辑块寻址) 如何将 LBA 地址转换为…...
,服务网格(Service Mesh)以及无服务器运算Serverless简单介绍)
微服务(Microservices),服务网格(Service Mesh)以及无服务器运算Serverless简单介绍
文章目录 什么是微服务?一、定义与特点二、优势三、组件与架构四、应用场景五、挑战与解决方案什么是服务网格?一、定义与特点二、核心组件三、主要功能四、实现工具五、应用场景六、优势与挑战什么是Serverless?一、定义与特点二、主要领域三、优势四、应用场景五、挑战三者…...

【AIGC】AI时代的数据安全:使用ChatGPT时的自查要点
博客主页: [小ᶻZ࿆] 本文专栏: AIGC | ChatGPT 文章目录 💯前言💯法律法规背景中华人民共和国保守秘密法中华人民共和国网络安全法中华人民共和国个人信息保护法遵守法律法规的重要性 💯ChatGPT的数据使用特点ChatGPT数据安全…...

什么是区块链桥?
什么是区块链桥? 区块链桥是一种实现资产从一个区块链转移至另一个区块链的工具,它解决了区块链技术中不同网络之间缺乏互操作性的问题。区块链桥通过创建代表另一区块链资产的合成衍生品,使得原本互不兼容的区块链资产能够相互连接和转移。…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
