线段树模板

线段树

练习题目

洛谷题单
【模板】线段树 1
【模板】线段树 2
开关
扶苏的问题

线段树概念

线段树是一种高级数据结构，与树状数组一样，被用来处理区间查询，修改问题，并且线段树的最大优点是对动态数据的处理十分高效。

来看看线段树能处理的问题：

• 求区间的修改。给你一个区间，让你查询区间的左节点 , 右节点和增加量。如果用普通的数组，加上m次询问，则时间复杂度将会达到接近O(mn)阶，是非常低效的。
• 区间和问题，查询，修改区间的元素，求和等等。使用普通数组对指定的区间求和，加之m次询问，则时间复杂度也会达到O(mn)，也可以使用前缀和求区间和，但是前缀和虽然高效，但是远没有线段树灵活，线段树能够处理的问题是非常多的。
• 线段树对于以上两种问题求解都具有O(mlogn)的时间复杂度，是非常高效的。

---

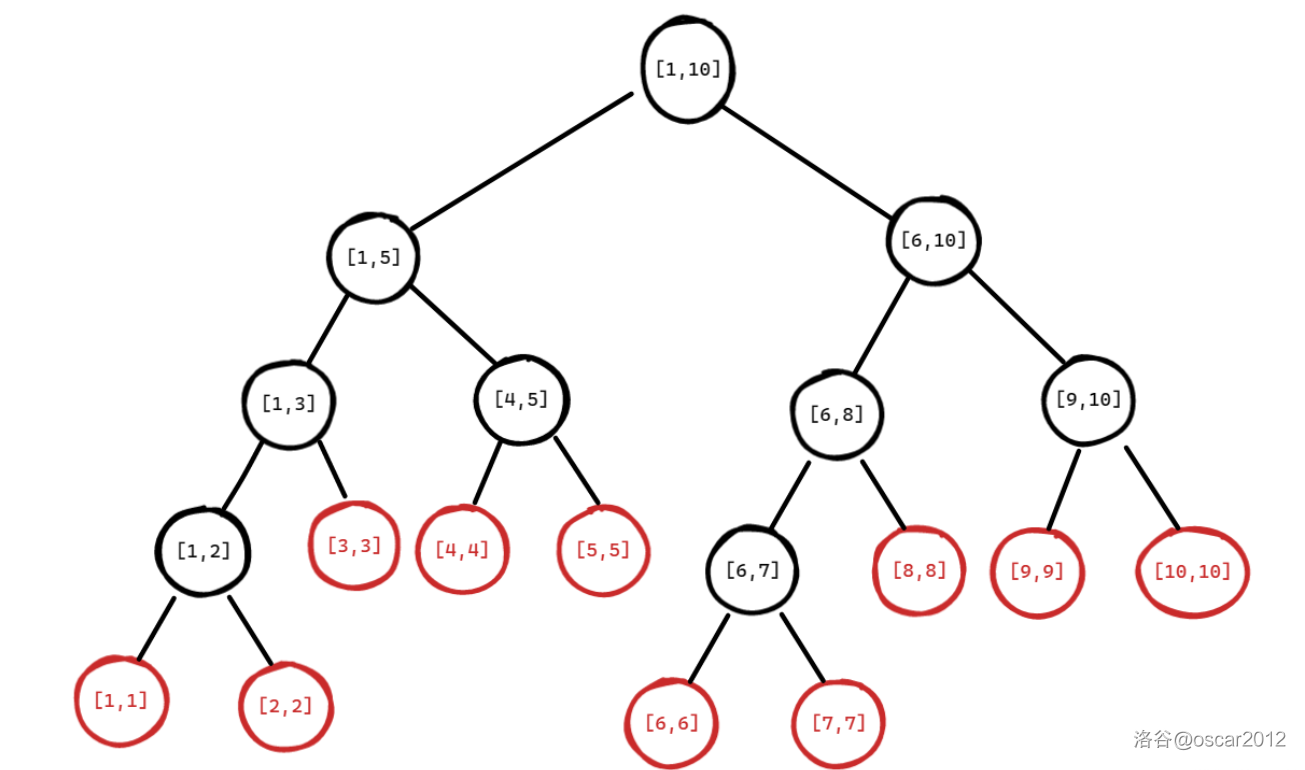
线段树是具有以下形态的二叉树，其中树上的每个节点都是一个线段区间 。

看图可以发现线段树的几个特征：

这颗二叉树是采用分治法来划分区间，并且构建子树的，左右子树各一半。

这颗二叉树的每个节点都是一个线段区间，非叶子节点的线段区间是一段不相等的区间，叶子节点的线段区间的只包含一个元素。

区间维护

求区间维护是线段树最常用的使用方法之一,一共有五类函数:

• 辅助函数（前置准备，上移与下移）: update ，pushdown
• 创建线段树 ：build
• 修改线段树 ：modify
• 查询线段树 ：query
• 更新线段树 ：update

辅助函数

inline void update(int root)
{node[root].sum = node[root * 2].sum + node[root * 2 + 1].sum;//将左子树和右子树的值合并
}inline void pushdown(int root)
{int lazy = node[root].lazy;node[root * 2].lazy += lazy;node[root * 2].sum += (node[root * 2].r - node[root * 2].l + 1) * lazy;//下发懒惰标记node[root * 2 + 1].lazy += lazy;node[root * 2 + 1].sum += (node[root * 2 + 1].r - node[root * 2 + 1].l + 1) * lazy;//下发懒惰标记node[root].lazy = 0;//清空懒惰标记
}

创建线段树 ：build

void build_tree(int root, int l, int r)
{node[root].l = l;//封装左区间node[root].r = r;//封装右区间if (l == r){node[root].sum = a[l];//大小与需要相同,就赋值return;}int mid = (l + r) >> 1;build_tree(root * 2, l, mid);//递归左子树build_tree(root * 2 + 1, mid + 1, r);//递归右子树update(root);//合并左右子树
}

修改线段树 ：modify

void modify(int root, int l, int r, int k)
{if (node[root].l == l && node[root].r == r){node[root].sum += (r - l + 1) * k;//值加上区间内增加的值node[root].lazy += k;//懒惰标记return;}pushdown(root);//下发懒惰标记,因为接下来要访问左右子树int mid = (node[root].l + node[root].r) >> 1;//取中间节点if (r <= mid){modify(root * 2, l, r, k);//全在左边的情况,递归左子树}else if (l > mid)全在右边的情况,递归右子树{modify(root * 2 + 1, l, r, k);}else//负责左右都递归{modify(root * 2, l, mid, k);modify(root * 2 + 1, mid + 1, r, k);}update(root);//因为修改了左右子树,所以要合并左右子树return;
}

查询线段树：query

long long query(int root, int l, int r)
{if (node[root].l == l && node[root].r == r){return node[root].sum;//如果区间正好吻合,则返回原值}pushdown(root);//下发懒惰标记,因为接下来要访问左右子树int mid = (node[root].l + node[root].r) >> 1;if (r <= mid)//同modify中的递归{return query(root * 2, l, r);}else if (l > mid){return query(root * 2 + 1, l, r);}return query(root * 2, l, mid) + query(root * 2 + 1, mid + 1, r);//这里要返回和
}

全部代码

#include <bits/stdc++.h>
using namespace std;struct tree
{int l, r;long long sum, lazy;
} node[300010];int n, m;
int a[100010];inline void update(int root)
{node[root].sum = node[root * 2].sum + node[root * 2 + 1].sum;//将左子树和右子树的值合并
}inline void pushdown(int root)
{int lazy = node[root].lazy;node[root * 2].lazy += lazy;node[root * 2].sum += (node[root * 2].r - node[root * 2].l + 1) * lazy;//下发懒惰标记node[root * 2 + 1].lazy += lazy;node[root * 2 + 1].sum += (node[root * 2 + 1].r - node[root * 2 + 1].l + 1) * lazy;//下发懒惰标记node[root].lazy = 0;//清空懒惰标记
}
void build_tree(int root, int l, int r)
{node[root].l = l;//封装左区间node[root].r = r;//封装右区间if (l == r){node[root].sum = a[l];//大小与需要相同,就赋值return;}int mid = (l + r) >> 1;build_tree(root * 2, l, mid);//递归左子树build_tree(root * 2 + 1, mid + 1, r);//递归右子树update(root);//合并左右子树
}void modify(int root, int l, int r, int k)
{if (node[root].l == l && node[root].r == r){node[root].sum += (r - l + 1) * k;//值加上区间内增加的值node[root].lazy += k;//懒惰标记return;}pushdown(root);//下发懒惰标记,因为接下来要访问左右子树int mid = (node[root].l + node[root].r) >> 1;//取中间节点if (r <= mid){modify(root * 2, l, r, k);//全在左边的情况,递归左子树}else if (l > mid)全在右边的情况,递归右子树{modify(root * 2 + 1, l, r, k);}else//负责左右都递归{modify(root * 2, l, mid, k);modify(root * 2 + 1, mid + 1, r, k);}update(root);//因为修改了左右子树,所以要合并左右子树return;
}long long query(int root, int l, int r)
{if (node[root].l == l && node[root].r == r){return node[root].sum;//如果区间正好吻合,则返回原值}pushdown(root);//下发懒惰标记,因为接下来要访问左右子树int mid = (node[root].l + node[root].r) >> 1;if (r <= mid)//同modify中的递归{return query(root * 2, l, r);}else if (l > mid){return query(root * 2 + 1, l, r);}return query(root * 2, l, mid) + query(root * 2 + 1, mid + 1, r);//这里要返回和
}
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}build_tree(1, 1, n);//建树while (m--){long long op, x, y, k;cin >> op >> x >> y;if (op == 1){cin >> k;modify(1, x, y, k);//区间修改}else if (op == 2){cout << query(1, x, y) << endl;//区间查询}}return 0;
}