吉如一线段树:区间最值和历史最值
区间最值和历史最值
问题一
给定一个长度为 n n n 的数组 a a a , 实现以下三种操作 :
0 l r x: 将 a r r [ l ∼ r ] arr[l\sim r] arr[l∼r] 范围的每个数 v v v , 更新为 min ( v , x ) \min (v, x) min(v,x)
1 l r: 查询 max i = l r a r r i \max_{i=l}^r arr_i maxi=lrarri
2 l r: 查询 ∑ i = l r a r r i \sum_{i=l}^rarr_i ∑i=lrarri
吉如一线段树。
#include<bits/stdc++.h>
using namespace std;
#define int long long#define lc u << 1
#define rc u << 1 | 1int const N = 5e5 + 10;struct node{// mx : 最大值 ; cnt : mx 出现次数// se : 第二大// sum : 区间和int l, r, mx, cnt, se, sum;
}tr[N << 2];int a[N];void pushup(int u){tr[u].sum = tr[lc].sum + tr[rc].sum;tr[u].mx = max(tr[lc].mx, tr[rc].mx);if(tr[lc].mx == tr[rc].mx){tr[u].cnt = tr[lc].cnt + tr[rc].cnt;tr[u].se = max(tr[lc].se, tr[rc].se);}else if(tr[lc].mx > tr[rc].mx){tr[u].cnt = tr[lc].cnt;tr[u].se = max(tr[lc].se, tr[rc].mx);}else{tr[u].cnt = tr[rc].cnt;tr[u].se = max(tr[lc].mx, tr[rc].se);}
}void pushdown(int u){if(tr[lc].mx > tr[u].mx){ // 标记回收tr[lc].sum -= (tr[lc].mx - tr[u].mx) * tr[lc].cnt;tr[lc].mx = tr[u].mx;}if(tr[rc].mx > tr[u].mx){ // 标记回收tr[rc].sum -= (tr[rc].mx - tr[u].mx) * tr[rc].cnt;tr[rc].mx = tr[u].mx;}
}void build(int u, int l, int r){tr[u] = {l, r, a[l], 1, LLONG_MIN, a[l]};if(l == r) return ;int mid = l + r >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(u);
}void setMin(int u, int l, int r, int x){if(x >= tr[u].mx) return ;if(l <= tr[u].l && r >= tr[u].r && x > tr[u].se){tr[u].sum -= (tr[u].mx - x) * tr[u].cnt;tr[u].mx = x;return ;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if(l <= mid) setMin(lc, l, r, x);if(r > mid) setMin(rc, l, r, x);pushup(u);
}int askMax(int u, int l, int r){if(l <= tr[u].l && r >= tr[u].r){return tr[u].mx;}int mid = tr[u].l + tr[u].r >> 1;pushdown(u);int res = LLONG_MIN;if(l <= mid) res = max(res, askMax(lc, l, r));if(r > mid) res = max(res, askMax(rc, l, r));return res;
}int askSum(int u, int l, int r){if(l <= tr[u].l && r >= tr[u].r){return tr[u].sum;}int mid = tr[u].l + tr[u].r >> 1;pushdown(u);int sum = 0;if(l <= mid) sum += askSum(lc, l, r);if(r > mid) sum += askSum(rc, l, r);return sum;
}void solve(){int n, q;cin >> n >> q;for(int i = 1; i <= n; i ++){cin >> a[i];}build(1, 1, n);while(q --){int op, l, r, t;cin >> op >> l >> r;if(op == 0){cin >> t;setMin(1, l, r, t);}else if(op == 1){cout << askMax(1, l, r) << '\n';}else{cout << askSum(1, l, r) << '\n';}}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); int T;cin >> T;while(T --){solve();}return 0;
}
问题二
题目背景
本题是线段树维护区间最值操作与区间历史最值的模板。
题目描述
给出一个长度为 n n n 的数列 A A A,同时定义一个辅助数组 B B B, B B B 开始与 A A A 完全相同。接下来进行了 m m m 次操作,操作有五种类型,按以下格式给出:
1 l r k:对于所有的 i ∈ [ l , r ] i\in[l,r] i∈[l,r],将 A i A_i Ai 加上 k k k( k k k 可以为负数)。2 l r v:对于所有的 i ∈ [ l , r ] i\in[l,r] i∈[l,r],将 A i A_i Ai 变成 min ( A i , v ) \min(A_i,v) min(Ai,v)。3 l r:求 ∑ i = l r A i \sum_{i=l}^{r}A_i ∑i=lrAi。4 l r:对于所有的 i ∈ [ l , r ] i\in[l,r] i∈[l,r],求 A i A_i Ai 的最大值。5 l r:对于所有的 i ∈ [ l , r ] i\in[l,r] i∈[l,r],求 B i B_i Bi 的最大值。
在每一次操作后,我们都进行一次更新,让 B i ← max ( B i , A i ) B_i\gets\max(B_i,A_i) Bi←max(Bi,Ai)。
输入格式
第一行包含两个正整数 n , m n,m n,m,分别表示数列 A A A 的长度和操作次数。
第二行包含 n n n 个整数 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An,表示数列 A A A。
接下来 m m m 行,每行行首有一个整数 o p op op,表示操作类型;接下来两个或三个整数表示操作参数,格式见【题目描述】。
输出格式
对于 o p ∈ { 3 , 4 , 5 } op\in\{3,4,5\} op∈{3,4,5} 的操作,输出一行包含一个整数,表示这个询问的答案。
样例 #1
样例输入 #1
5 6
1 2 3 4 5
3 2 5
1 1 3 3
4 2 4
2 3 4 1
5 1 5
3 1 4
样例输出 #1
14
6
6
11
提示
样例说明 #1
| 操作次数 | 输入内容 | 操作 | 数列 | 输出结果 |
|---|---|---|---|---|
| 0 | 1 , 2 , 3 , 4 , 5 1,2,3,4,5 1,2,3,4,5 | |||
| 1 | 3 2 5 | 求出 [ 2 , 5 ] [2,5] [2,5] 所有数的和 | 1 , 2 , 3 , 4 , 5 1,2,3,4,5 1,2,3,4,5 | 14 |
| 2 | 1 1 3 3 | 将 [ 1 , 3 ] [1,3] [1,3] 内所有数加 3 3 3 | 4 , 5 , 6 , 4 , 5 4,5,6,4,5 4,5,6,4,5 | |
| 3 | 4 2 4 | 求出 [ 2 , 4 ] [2,4] [2,4] 所有数的最大值 | 4 , 5 , 6 , 4 , 5 4,5,6,4,5 4,5,6,4,5 | 6 |
| 4 | 2 3 4 1 | 将 [ 3 , 4 ] [3,4] [3,4] 所有数与 1 1 1 取最小值 | 4 , 5 , 1 , 1 , 5 4,5,1,1,5 4,5,1,1,5 | |
| 5 | 5 1 5 | 求出 [ 1 , 5 ] [1,5] [1,5] 所有位置历史最大值的最大值 | 4 , 5 , 1 , 1 , 5 4,5,1,1,5 4,5,1,1,5 | 6 |
| 6 | 3 1 4 | 求出 [ 1 , 4 ] [1,4] [1,4] 所有数的和 | 4 , 5 , 1 , 1 , 5 4,5,1,1,5 4,5,1,1,5 | 11 |
数据规模与约定
- 对于测试点 1 , 2 1,2 1,2,满足 n , m ≤ 5000 n,m\leq 5000 n,m≤5000;
- 对于测试点 3 , 4 3,4 3,4,满足 o p ∈ { 1 , 2 , 3 , 4 } op\in\{1,2,3,4\} op∈{1,2,3,4};
- 对于测试点 5 , 6 5,6 5,6,满足 o p ∈ { 1 , 3 , 4 , 5 } op\in\{1,3,4,5\} op∈{1,3,4,5};
- 对于全部测试数据,保证 1 ≤ n , m ≤ 5 × 1 0 5 1\leq n,m\leq 5\times 10^5 1≤n,m≤5×105, − 5 × 1 0 8 ≤ A i ≤ 5 × 1 0 8 -5\times10^8\leq A_i\leq 5\times10^8 −5×108≤Ai≤5×108, o p ∈ [ 1 , 5 ] op\in[1,5] op∈[1,5], 1 ≤ l ≤ r ≤ n 1 \leq l\leq r \leq n 1≤l≤r≤n, − 2000 ≤ k ≤ 2000 -2000\leq k\leq 2000 −2000≤k≤2000, − 5 × 1 0 8 ≤ v ≤ 5 × 1 0 8 -5\times10^8\leq v\leq 5\times10^8 −5×108≤v≤5×108。
提示
本题输入量较大,请使用合理高效的读入方法。
#include<bits/stdc++.h>
using namespace std;
#define int long long#define lc u << 1
#define rc u << 1 | 1int const N = 5e5 + 10;struct node{// mx : 最大值 ; cnt : mx 出现次数// se : 第二大// sum : 区间和// mxhis : 历史最大值// add1, add2 : 区间最大值/非最大的懒标记// add3, add4 : 最大值懒标记历史最大值, 非最大值懒标记最历史大值int l, r, mx, cnt, se, sum, mxhis;int add1, add2, add3, add4;
}tr[N << 2];int a[N];void pushup(int u){tr[u].sum = tr[lc].sum + tr[rc].sum;tr[u].mx = max(tr[lc].mx, tr[rc].mx);tr[u].mxhis = max(tr[lc].mxhis, tr[rc].mxhis);if(tr[lc].mx == tr[rc].mx){tr[u].cnt = tr[lc].cnt + tr[rc].cnt;tr[u].se = max(tr[lc].se, tr[rc].se);}else if(tr[lc].mx > tr[rc].mx){tr[u].cnt = tr[lc].cnt;tr[u].se = max(tr[lc].se, tr[rc].mx);}else{tr[u].cnt = tr[rc].cnt;tr[u].se = max(tr[lc].mx, tr[rc].se);}
}void down(int u, int add1, int add2, int add3, int add4){tr[u].sum += add1 * tr[u].cnt + add2 * (tr[u].r - tr[u].l + 1 - tr[u].cnt);tr[u].mxhis = max(tr[u].mxhis, tr[u].mx + add3);tr[u].mx += add1;if(tr[u].se != LLONG_MIN) tr[u].se += add2;tr[u].add3 = max(tr[u].add3, tr[u].add1 + add3);tr[u].add4 = max(tr[u].add4, tr[u].add2 + add4);tr[u].add1 += add1;tr[u].add2 += add2;
}void pushdown(int u){int maxn = max(tr[lc].mx, tr[rc].mx);if(tr[lc].mx == maxn){down(lc, tr[u].add1, tr[u].add2, tr[u].add3, tr[u].add4);}else{down(lc, tr[u].add2, tr[u].add2, tr[u].add4, tr[u].add4);}if(tr[rc].mx == maxn){down(rc, tr[u].add1, tr[u].add2, tr[u].add3, tr[u].add4);}else{down(rc, tr[u].add2, tr[u].add2, tr[u].add4, tr[u].add4);}tr[u].add1 = tr[u].add2 = tr[u].add3 = tr[u].add4 = 0;
}void build(int u, int l, int r){tr[u] = {l, r, a[l], 1, LLONG_MIN, a[l], a[l], 0, 0, 0, 0};if(l == r) return ;int mid = l + r >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(u);
}void segAdd(int u, int l, int r, int x){if(l <= tr[u].l && r >= tr[u].r){tr[u].sum += x * (tr[u].r - tr[u].l + 1);tr[u].mx += x;tr[u].mxhis = max(tr[u].mx, tr[u].mxhis);if(tr[u].se != LLONG_MIN) tr[u].se += x;tr[u].add1 += x, tr[u].add2 += x;tr[u].add3 = max(tr[u].add3, tr[u].add1);tr[u].add4 = max(tr[u].add4, tr[u].add2);return ;}int mid = tr[u].l + tr[u].r >> 1;pushdown(u);if(l <= mid) segAdd(lc, l, r, x);if(r > mid) segAdd(rc, l, r, x);pushup(u);
}void setMin(int u, int l, int r, int x){if(x >= tr[u].mx) return ;if(l <= tr[u].l && r >= tr[u].r && x > tr[u].se){int t = tr[u].mx - x;tr[u].sum -= t * tr[u].cnt;tr[u].mx = x;tr[u].add1 -= t;return ;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if(l <= mid) setMin(lc, l, r, x);if(r > mid) setMin(rc, l, r, x);pushup(u);
}int askMax(int u, int l, int r){if(l <= tr[u].l && r >= tr[u].r){return tr[u].mx;}int mid = tr[u].l + tr[u].r >> 1;pushdown(u);int res = LLONG_MIN;if(l <= mid) res = max(res, askMax(lc, l, r));if(r > mid) res = max(res, askMax(rc, l, r));return res;
}int askMaxHis(int u, int l, int r){if(l <= tr[u].l && r >= tr[u].r){return tr[u].mxhis;}int mid = tr[u].l + tr[u].r >> 1;pushdown(u);int res = LLONG_MIN;if(l <= mid) res = max(res, askMaxHis(lc, l, r));if(r > mid) res = max(res, askMaxHis(rc, l, r));return res;
}int askSum(int u, int l, int r){if(l <= tr[u].l && r >= tr[u].r){return tr[u].sum;}int mid = tr[u].l + tr[u].r >> 1;pushdown(u);int sum = 0;if(l <= mid) sum += askSum(lc, l, r);if(r > mid) sum += askSum(rc, l, r);return sum;
}void solve(){int n, q;cin >> n >> q;for(int i = 1; i <= n; i ++){cin >> a[i];}build(1, 1, n);while(q --){int op, l, r, t;cin >> op >> l >> r;if(op == 1){cin >> t;segAdd(1, l, r, t);}else if(op == 2){cin >> t;setMin(1, l, r, t);}else if(op == 3){cout << askSum(1, l, r) << '\n';}else if(op == 4){cout << askMax(1, l, r) << '\n';}else{cout << askMaxHis(1, l, r) << '\n';}}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); int T = 1;while(T --){solve();}return 0;
}相关文章:

吉如一线段树:区间最值和历史最值
区间最值和历史最值 问题一 给定一个长度为 n n n 的数组 a a a , 实现以下三种操作 : 0 l r x : 将 a r r [ l ∼ r ] arr[l\sim r] arr[l∼r] 范围的每个数 v v v , 更新为 min ( v , x ) \min (v, x) min(v,x) 1 l r : 查询 max i l r a r r i \max_{il}^r ar…...

数据库常见的安全特性有哪些
数据库的安全特性主要包括以下几个方面,以确保数据的机密性、完整性和可用性: 1. 身份验证(Authentication) 数据库系统会通过身份验证来确定用户的身份,常见的方式有用户名/密码验证、基于证书的验证、多因素验证&a…...

Debezium日常分享系列之:Debezium 3.0.0.Final发布
Debezium日常分享系列之:Debezium 3.0.0.Final发布 Debezium 核心的变化需要 Java 17基于Kafka 3.8 构建废弃的增量信号字段的删除每个表的详细指标 MariaDB连接器的更改版本 11.4.3 支持 MongoDB连接器的更改MongoDB sink connector MySQL连接器的改变MySQL 9MySQL…...
)
MVCC(多版本并发控制)
目录 1.MVCC的工作原理2.MVCC的优点3.例子 MVCC(多版本并发控制)是一种用于数据库管理系统中实现并发控制的技术。它允许多个事务同时对数据库进行读写操作,而不会相互干扰,从而提高数据库系统的性能和可用性。MVCC通过为每个事务…...
低代码可视化-uniapp响应式数据data-代码生成器
在uniapp框架中,data 是一个核心的概念,它代表了组件或uniapp实例中的响应式数据。这些数据是组件状态的基础,uniapp会根据这些数据的变化来更新DOM,从而保持视图与数据的同步。 data 的特点 响应式:uniapp使用一种称…...
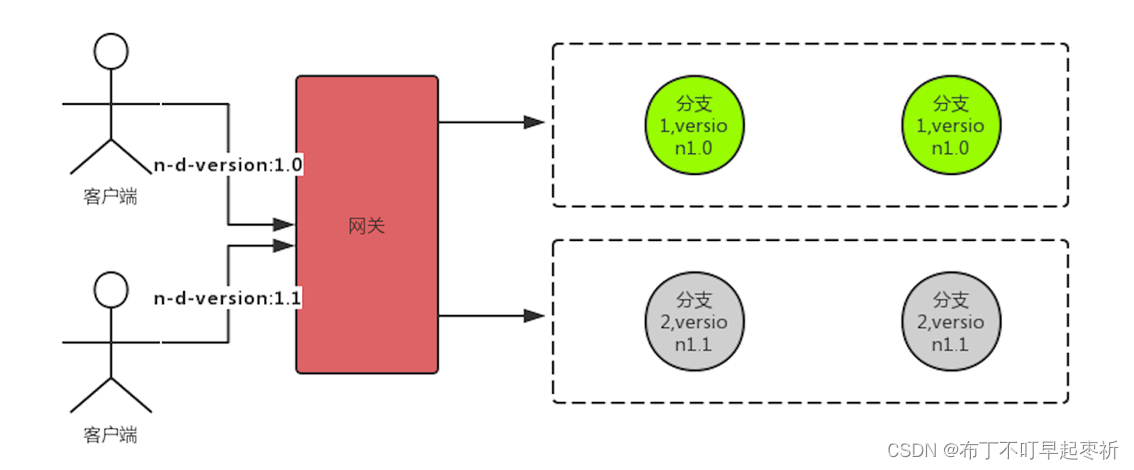
10.7学习
1.安全认证 ●Session 认证中最常用的一种方式,也是最简单的。存在多节点session丢失的情况,可通过nginx粘性Cookie和Redis集中式Session存储解决 ●HTTP Basic Authentication 服务端针对请求头中base64加密的Authorization 和用户名和密码进行校验。…...

基础算法之前缀和--Java实现(下)--LeetCode题解:-和为 K 的子数组 - 和可被 K 整除的子数组 -连续数组-矩阵区域和
这里是Themberfue 和为 K 的子数组 题目解析 返回子数组中所有元素的和等于给定k的个数。 算法讲解 这题好像是用滑动窗口解决,但其实不能,因为 nums 中的元素可能存在负数,就不能保证其单调性的性质。 用前缀和求也不易想到,…...

序列化与反序列化基础及反序列化漏洞(附案例)
参考文章: [web安全原理]PHP反序列化漏洞 - 笑花大王 - 博客园 (cnblogs.com) 一、概念 为了能有效的存储数据而不丢失数据的类型和内容,经常需要通过序列化对数据进行处理,将数据进行序列化后,会生成一个字符串,字符…...

Khronos:动态环境下时空度量语义SLAM的统一方法
Khronos: A Unified Approach for Spatio-Temporal Metric-Semantic SLAM in Dynamic Environments 原文 项目 引言: 人类居住环境通常是高度动态的,人、机器人和其他实体不断移动、互动和改变场景。对于机器人在这种情况下的操作,仅仅建立一…...

一个迷茫的25岁前端程序员的自述
作者:一尾流莺 一直听说程序员的危机在 35 岁,没想到我的危机从 25 岁就开始了。 我甚至不知道自己是不是 25 岁,也可能是 26 岁,或者 27 岁,1998 年的生日,按照 2023 - 1998 的算法就是 25,按…...

多文件并发多线程MD5工具(相对快速的MD5一批文件),适配自定义MD5 Hash I/O缓存。
自己写的多文件 MD5校验工具,一个文件开一个线程,有最大I/O 缓存设置,兼容读写MD5后缀文件。 共计91个文件,合计180G左右 12分钟左右,UI基本卡废,但程序没蹦,属于正常。 卡的原因是基本是用 I/O…...

Pikachu-url重定向-不安全的url跳转
不安全的url跳转 不安全的url跳转问题可能发生在一切执行了url地址跳转的地方。如果后端采用了前端传进来的(可能是用户传参,或者之前预埋在前端页面的url地址)参数作为了跳转的目的地,而又没有做判断的话就可能发生"跳错对象"的问题。 url跳转比较直接的危害是: …...

如何下载和安装CLion,图文详解
一、下载 登录JetBrains官网,下载最新版本的Clion,Clion目前没有社区版,都是专业版。 二、安装 1、启动Clion安装程序,下一步。 2、修改安装目录,下一步。 3、创建桌面快捷方式,更新PATH变量࿰…...

vue3导入本地图片2种实现方法
在<script setup>中使用import语法: <template><img :src"logo" alt"Logo"> </template><script setup> import logo from ./assets/logo.png; </script> 使用Vue的ref来动态地在<script setup>中…...
))
leetcode 刷题day36动态规划Part05 背包问题(完全背包、518. 零钱兑换 II、377. 组合总和 Ⅳ、70. 爬楼梯 (进阶))
完全背包 完全背包的每件商品都有无限个,和01背包的一不同主要体现在遍历顺序上。为了保证每个物品仅被添加一次,01背包内嵌的循环是从大到小遍历。而完全背包的物品是可以添加多次的,所以要从小到大去遍历。 518. 零钱兑换 II 思路&#…...

检查jar冲突,查找存在相同class的jar
写在前面 本文看下如何查找jar冲突,即查找哪些jar包中存在相同的class。如果是存在相同jar的不同版本,基本一眼就能看出来,然后结合maven的依赖关系将其剔除掉即可,但是当你遇到了有人手动拷贝某些class到jar包中导致冲突的情况时…...

PhpStudy-PHP5.4.45后门漏洞应用程序(C++/base64/winhttp)
PhpStudy-PHP5.4.45后门漏洞应用程序(C/base64/winhttp) 前言引言(时间回到多年前) PhpShellCmd.exe使用介绍:(1)输入网址检测是否存在PHP/5.4.45(2)whoami(3…...

【优选算法】(第二十七篇)
目录 重排链表(medium) 题目解析 讲解算法原理 编写代码 合并K个升序链表(hard) 题目解析 讲解算法原理 编写代码 重排链表(medium) 题目解析 1.题目链接:. - 力扣(LeetCod…...
学习Flask框架
Flask简介 Flask是一个使用 Python 编写的轻量级 Web 应用框架。其 WSGI 工具箱采用 Werkzeug ,模板引擎则使用 Jinja2 。Flask使用 BSD 授权。 Flask也被称为 “microframework” ,因为它使用简单的核心,用 extension 增加其他功能。Flask没…...
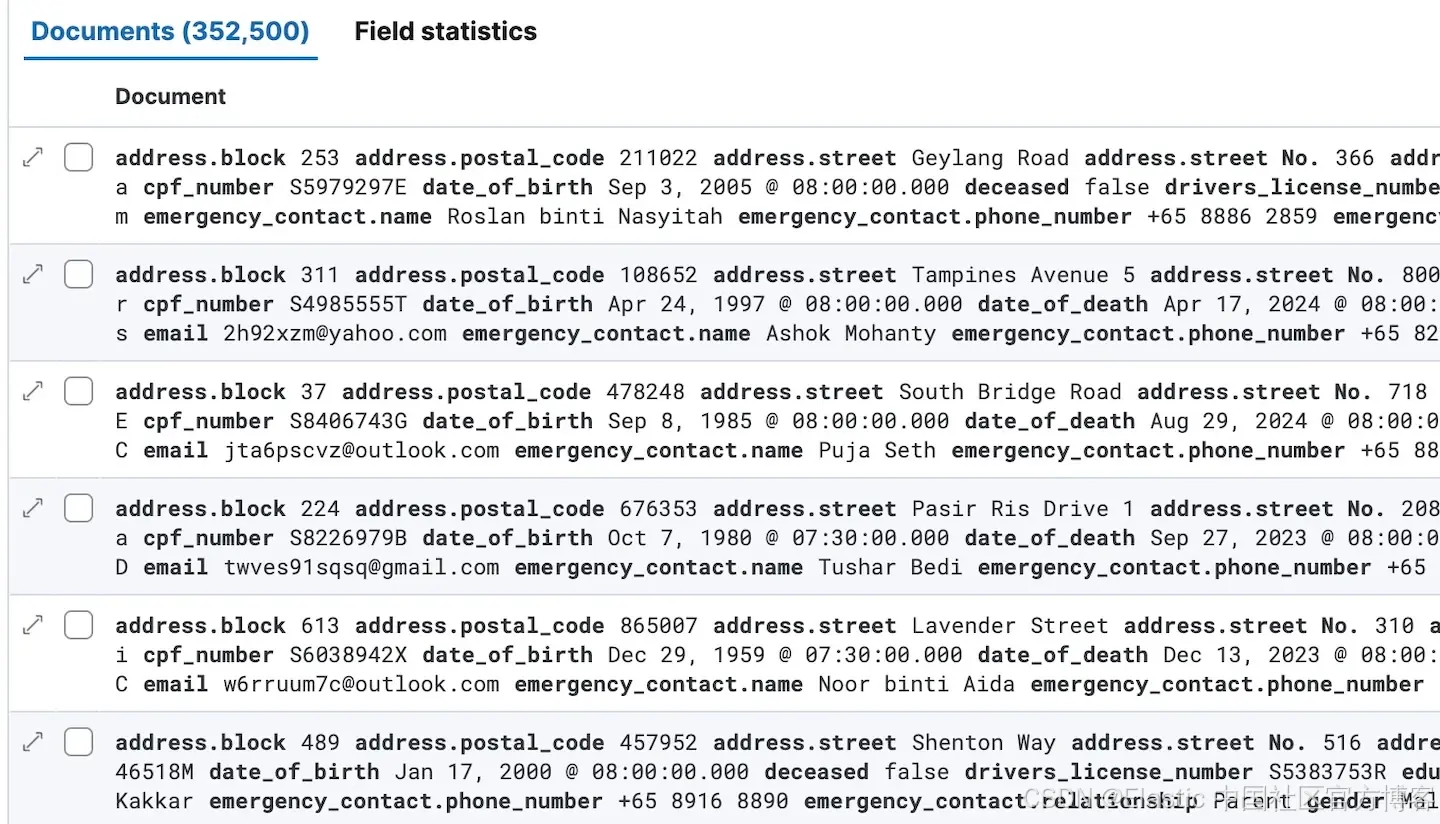
Elasticsearch:使用 LLM 实现传统搜索自动化
作者:来自 Elastic Han Xiang Choong 这篇简短的文章是关于将结构化数据上传到 Elastic 索引,然后将纯英语查询转换为查询 DSL 语句,以使用特定过滤器和范围搜索特定条件。完整代码位于此 Github repo 中。 首先,运行以下命令安装…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
