[控制理论]—差分变换法与双线性变换法的基本原理和代码实现
差分变换法与双线性变换法的基本原理和代码实现
1.差分变换法
差分变换法就是把微分方程中的导数用有限差分来近似等效,得到一个与原微分方程逼近的差分方程。
差分变换法包括后向差分与前向差分。
1.1 后向差分法
差分变换如下:
d e ( t ) d t = e ( k T ) − e ( k T − T ) T \frac{de(t)}{dt}=\frac{e(kT)-e(kT-T)}{T} dtde(t)=Te(kT)−e(kT−T)
对两边进行z变换,可得:
s = 1 − z − 1 T s=\frac{1-z^{-1}}{T} s=T1−z−1
后向差分变换法又称后向矩阵积分法,即用后向矩形面积来代替。因此当采样周期较大时,这种变换方法精度变差。
由变换过程可知:
- 若D(s)稳定,则D(z)一定稳定;对于不稳定的D(s),D(z)也有可能稳定。
- 由于后向差分变换不再满足z变换定义z=e^(sT),因此s平面与z平面的映射关系发生了改变,数字控制器D(z)的频率响应产生了较大的畸变。
严重的频率映射畸变导致变换精度下降,使后向差分变换的应用受到了一定限制,但当系统性能要求不是很高时,后向差分也起到一定作用。
例:
D ( s ) = 20 s + 80 s + 10 , T = 0.015 D(s) = \frac{20s+80}{s+10},T=0.015 D(s)=s+1020s+80,T=0.015
采用后向差分,代入下式:
s = 1 − z − 1 T s=\frac{1-z^{-1}}{T} s=T1−z−1
可得:
D ( z ) = U ( z ) E ( z ) = 21.2 − 20 z − 1 1.15 − z − 1 D(z) = \frac{U(z)}{E(z)}=\frac{21.2-20z^{-1}}{1.15-z^{-1}} D(z)=E(z)U(z)=1.15−z−121.2−20z−1
进行z反变换,可得:
u ( k ) = 0.87 u ( k − 1 ) + 18.43 e ( k ) − 17.39 e ( k − 1 ) u(k)=0.87u(k-1)+18.43e(k)-17.39e(k-1) u(k)=0.87u(k−1)+18.43e(k)−17.39e(k−1)
进一步探究采样频率对系统映射的影响,matlab代码如下:
numerator = [20, 80];
denominator = [1, 10];
G = tf(numerator, denominator);G_discrete1 = c2d(G, 0.01, 'foh');
G_discrete2 = c2d(G, 0.001, 'foh');
G_discrete3 = c2d(G, 0.0001, 'foh');figure;
hold on; bode(G, G_discrete1, G_discrete2, G_discrete3);
所得bode图为:

由bode图可知,当采样频率为0.01时,离散系统有较大影响;当采样频率为0.001甚至更高时,离散系统基本能反应连续系统的特性。
通过后向差分设计一个PID控制器,C语言伪代码实现如下:
// PID参数
#define KP 1.0f // 比例增益
#define KI 0.1f // 积分增益
#define KD 0.05f // 微分增益// 控制变量
float setpoint = 100.0f; // 目标速度
float currentSpeed = 0.0f; // 实际速度
float previousSpeed = 0.0f; // 上一速度
float integral = 0.0f; // 积分值
float lastTime = 0.0f; // 上次计算时间
float deltaTime = 0.1f; // 计算周期,假设为0.1秒void PID_Controller() {float error = setpoint - currentSpeed;integral += error * deltaTime;float derivative = (currentSpeed - previousSpeed) / deltaTime;float output = (KP * error) + (KI * integral) - (KD * derivative);// 更新电机控制信号(假设控制信号范围为0-255)if (output > 255) {output = 255;} else if (output < 0) {output = 0;}setMotorSpeed((uint8_t)output);previousSpeed = currentSpeed;
}void readCurrentSpeed() {currentSpeed = getMotorSpeedFromEncoder();
}int main(void) {while (1) {readCurrentSpeed(); PID_Controller(); Delay(100); }
}
verilog实现如下,输出限幅等功能未实现:
module PID_Controller (input wire clk, // 时钟信号input wire rst, // 复位信号input wire [15:0] setpoint, // 目标值input wire [15:0] current_value, // 当前值output reg [15:0] control_output // 控制输出
);parameter [15:0] KP = 16'd2; // 比例增益
parameter [15:0] KI = 16'd1; // 积分增益
parameter [15:0] KD = 16'd1; // 微分增益reg [15:0] error; // 误差
reg [15:0] previous_value; // 上一时刻的当前值
reg [31:0] integral; // 积分值
reg [15:0] derivative; // 微分值always @(posedge clk or posedge rst) beginif (rst) begincontrol_output <= 16'd0;previous_value <= 16'd0; integral <= 32'd0; end else beginerror <= setpoint - current_value;integral <= integral + error;derivative <= current_value - previous_value;control_output <= (KP * error) + (KI * integral[15:0]) - (KD * derivative);previous_value <= current_value;end
end
endmodule1.2 前向差分法
前向差分变换原理:
d e ( t ) d t = e ( k T + T ) − e ( k T ) T \frac{de(t)}{dt}=\frac{e(kT+T)-e(kT)}{T} dtde(t)=Te(kT+T)−e(kT)
进行z变换可得:
s = z − 1 T s = \frac{z-1}{T} s=Tz−1
前向差分性质如下:
- 若D(s)稳定,则D(z)不一定稳定。
- 数字控制器D(z)的频率响应会产生较大畸变。
因此,前向差分很少被使用。
2.双线性变换法
双线性变化法又被称为Tustin变换法,推导过程如下:
z = e T s = e T s / 2 − T s / 2 z = e^{Ts}=e^{\frac{Ts/2}{-Ts/2}} z=eTs=e−Ts/2Ts/2
对e^(Ts/2)部分进行泰勒级数展开,并取前两项近似:
z = 2 / T + s 2 / T − s z = \frac{2/T+s}{2/T-s} z=2/T−s2/T+s
得到双线性变换法的计算公式为:
s = 2 T z − 1 z + 1 s = \frac{2}{T}\frac{z-1}{z+1} s=T2z+1z−1
双线性变换的特点为:
- 若D(s)稳定,则D(z)也稳定。
- 变换前后的频率响应发生畸变。
- 不存在频率混叠现象。
对matlab函数c2d进行简要说明;
c2d:将模型从连续时间转换为离散时间
sysd = c2d(sysc,Ts,method)指定离散化方法离散化方法,指定为以下值之一:
'zoh'- 零阶保持(默认值)。假定控制输入在采样时间周期Ts内是分段常量。'foh'- 三角形逼近(修正一阶保持)。假定控制输入在采样时间周期Ts内是分段线性值。'impulse'- 冲激不变离散化'tustin'- 双线性(突斯汀)方法。要使用频率预修正指定此方法(以前称为'prewarp'方法),请使用c2dOptions的PrewarpFrequency选项。'matched'- 零极点匹配法'least-squares'- 最小二乘法'damped'- 仅基于稀疏模型的TRBDF2公式的阻尼突斯汀逼近。
首先对比相同采样频率下使用后向差分与双线性变换的性能影响:
numerator = [20, 80];
denominator = [1, 10];
G = tf(numerator, denominator);G_discrete1 = c2d(G, 0.015, 'foh');
G_discrete2 = c2d(G, 0.015, 'tustin');figure;
hold on; bode(G, G_discrete1, G_discrete2);
由bode图可知,在该采样频率下,双线性变换与差分变化作用效果近似。

将采样频率降低到0.15:
numerator = [20, 80];
denominator = [1, 10];
G = tf(numerator, denominator);G_discrete1 = c2d(G, 0.15, 'foh');
G_discrete2 = c2d(G, 0.15, 'tustin');figure;
hold on; bode(G, G_discrete1, G_discrete2);
观察bode图,此时使用双线性变化效果优于后向差分:

使用chatGPT对比这两种方法:
后向差分(Backward Difference)和双线性差分(Bilinear Difference)是数值分析中常用的差分方法,它们在不同的场景下各有优势。下面分别分析这两种方法的适用场景及优劣。
- 后向差分的优势场景
- 稳定性要求高的系统:
- 后向差分法是稳定的,尤其适合处理刚性系统。刚性系统的特点是某些动态特性变化非常快,这使得普通的显式方法难以稳定计算。后向差分能有效避免不稳定现象。
- 计算时间延迟的情况:
- 在一些实时系统中,后向差分法可以使用最新的已知数据点来估计当前状态,这在需要延迟计算的系统中非常有用,如控制系统中的实时反馈。
- 简单实现:
- 对于线性时间不变系统,后向差分的实现较为简单,特别是在不需要复杂的求解算法时。
- 误差控制:
- 后向差分通常能更好地控制截断误差,尤其在时间步长较大的情况下,避免了由大时间步带来的数值误差累积。
- 双线性差分的优势场景
- 高频动态响应:
- 双线性差分法能够更好地处理高频动态系统,尤其在需要高精度模拟频率响应特性的情况下,能够较好地保留系统的动态特性。
- 非线性系统的处理:
- 在处理非线性系统时,双线性差分法的表现往往优于后向差分。因为它能更有效地捕捉系统的变化,提供更准确的结果。
- 数值稳定性与精度的折中:
- 双线性差分法在保持数值稳定性的同时,能够提供更高的精度。特别是在需要优化精度的应用场景下,如电子电路模拟、信号处理等,双线性差分具有明显优势。
- 适应多种时间步长:
- 双线性差分能够更好地适应不同的时间步长,能够灵活应对多种动态情况,因此在自适应算法中较为常用。
- 总结
- 后向差分适合于需要稳定性和较简单实现的场合,尤其是在刚性系统和实时反馈控制中。
- 双线性差分适合于高频动态响应、非线性系统以及需要高精度的应用场合。
简而言之,后向差分已经适用于大部分场景,针对特殊情况,再考虑使用双线性差分。
C语言代码实现例子:
#include <stdio.h>double Kp = 1.0; // 比例增益
double Ki = 0.5; // 积分增益
double Kd = 0.1; // 微分增益// 采样周期
double Ts = 0.01;// PID控制器状态
double integral = 0.0; // 积分项
double prev_error = 0.0; // 上一时刻的误差double PID_Controller(double setpoint, double measured_value) {double error = setpoint - measured_value;integral += error * Ts;double derivative = (2 * (error - prev_error)) / Ts; // 双线性差分法计算微分double output = Kp * error + Ki * integral + Kd * derivative;prev_error = error;return output;
}
verilog代码:
module PID_Controller (input wire clk,input wire reset,input wire [15:0] setpoint, // 目标值input wire [15:0] measured_value, // 测量值output reg [15:0] control_signal // 控制信号输出
);parameter Kp = 16'd100; // 比例增益
parameter Ki = 16'd50; // 积分增益
parameter Kd = 16'd10; // 微分增益reg [15:0] integral;
reg [15:0] prev_error;
reg [15:0] error;
reg [15:0] derivative; always @(posedge clk or posedge reset) beginif (reset) beginintegral <= 0;prev_error <= 0;control_signal <= 0;end else beginerror <= setpoint - measured_value;integral <= integral + error;derivative <= (error - prev_error) * 2; control_signal <= (Kp * error + Ki * integral + Kd * derivative) >> 8; prev_error <= error;end
end
endmodule
相关文章:

[控制理论]—差分变换法与双线性变换法的基本原理和代码实现
差分变换法与双线性变换法的基本原理和代码实现 1.差分变换法 差分变换法就是把微分方程中的导数用有限差分来近似等效,得到一个与原微分方程逼近的差分方程。 差分变换法包括后向差分与前向差分。 1.1 后向差分法 差分变换如下: d e ( t ) d t e…...
【JavaEE】——多线程常用类
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 引入: 一:Callable和FutureTask类 1:对比Runnable 2:…...
Cilium-Multi Networking-多网络)
Cilium-实战系列-(二)Cilium-Multi Networking-多网络
一、Cilium必要开启的功能 1、enable-multi-network 2、ipam模式选择:multi-pool 二、涉及的CRD资源 1、 ciliumpodippools.cilium.io *通过Cilium管理节点上的pod cidr.网络分为主网络和第二网络。 *主网络的 ciliumpodippools.cilium.io default根据配置文件默认生成的。 …...
springboot自动配置
自动配置的核心就在SpringBootApplication注解上,SpringBootApplication这个注解 底层包含了3个注解,分别是: SpringBootConfiguration ComponentScan EnableAutoConfiguration EnableAutoConfiguration这个注解才是自动配置的核心,它 封…...

mock数据,不使用springboot的单元测试
业务代码 package com.haier.configure.service.impl;import com.baomidou.mybatisplus.core.toolkit.Wrappers; import com.baomidou.mybatisplus.extension.service.impl.ServiceImpl; import com.haier.common.util.RequestUtil; import com.haier.configure.entity.Langua…...
【pytorch】pytorch入门5:最大池化层(Pooling layers )
文章目录 前言一、定义概念 缩写二、参数三、最大池化操作四、使用步骤总结参考文献 前言 使用 B站小土堆课程 一、定义概念 缩写 池化(Pooling)是深度学习中常用的一种操作,用于降低卷积神经网络(CNN)或循环神经网…...

职场上的人情世故,你知多少?这五点一定要了解
职场是一个由人组成的复杂社交网络,人情世故在其中起着至关重要的作用。良好的人际关系可以帮助我们更好地融入团队,提升工作效率,甚至影响职业发展。在职场中,我们需要了解一些关键要素,以更好地处理人际关系…...

Python | Leetcode Python题解之第456题132模式
题目: 题解: class Solution:def find132pattern(self, nums: List[int]) -> bool:candidate_i, candidate_j [-nums[0]], [-nums[0]]for v in nums[1:]:idx_i bisect.bisect_right(candidate_i, -v)idx_j bisect.bisect_left(candidate_j, -v)if…...

【重学 MySQL】五十四、整型数据类型
【重学 MySQL】五十四、整型数据类型 整型类型TINYINTSMALLINTMEDIUMINTINT(或INTEGER)BIGINT 可选属性UNSIGNEDZEROFILL显示宽度(M)AUTO_INCREMENT注意事项 适合场景TINYINTSMALLINTMEDIUMINTINT(或INTEGER࿰…...

查看 Git 对象存储中的内容
查看 Git 对象存储中的内容 ls -C .git/objects/<dir>ls: 列出目录内容的命令。-C: 以列的形式显示内容。.git/objects/<dir>: .git 是存储仓库信息的 Git 目录,objects 是其中存储对象的子目录。<dir> 是对象存储目录下的一个特定的子目录。 此…...

Redis 中热 Key 的判定及其解决方案
引言 Redis 作为高效的内存数据库,常用于缓存、消息队列等场景。随着数据量和并发量的增加,某些数据的访问频率会远远高于其他数据,这些被频繁访问的 Key 被称为 热 Key。热 Key 问题是 Redis 应用中常见的性能瓶颈之一,它可能导…...

elasticsearch创建索引
1对比关系型数据库,创建索引就等同于创建数据库 在postman中,向ES服务器发PUT请求 显示已经创建成功了 http://192.168.1.108:9200/shopping 请求方式get http://192.168.1.108:9200/shopping 请求全部的index的url地址 get 请求 http://192.168.1.10…...

【STM32单片机_(HAL库)】4-2-1【定时器TIM】定时器输出PWM实现呼吸灯实验
1.硬件 STM32单片机最小系统LED灯模块 2.软件 pwm驱动文件添加定时器HAL驱动层文件添加GPIO常用函数定时器输出PWM配置步骤main.c程序 #include "sys.h" #include "delay.h" #include "led.h" #include "pwm.h"int main(void) {HA…...

计算机网络:物理层 —— 信道复用技术
文章目录 信道信道复用技术信道复用技术的作用基本原理常用的信道复用技术频分复用 FDM时分复用 TDM波分复用 WDM码分复用 CDM码片向量基本原理 信道 信道是指信息传输的通道或介质。在通信中,信道扮演着传输信息的媒介的角色,将发送方发送的信号传递给…...

期权懂|期权交易涨跌幅限制会随时调整吗?
本期让我懂 你就懂的期权懂带大家来了解,期权交易涨跌幅限制会随时调整吗?有兴趣的朋友可以看一下。期权小懂每日分享期权知识,帮助期权新手及时有效地掌握即市趋势与新资讯! 期权交易涨跌幅限制会随时调整吗? 涨跌幅…...
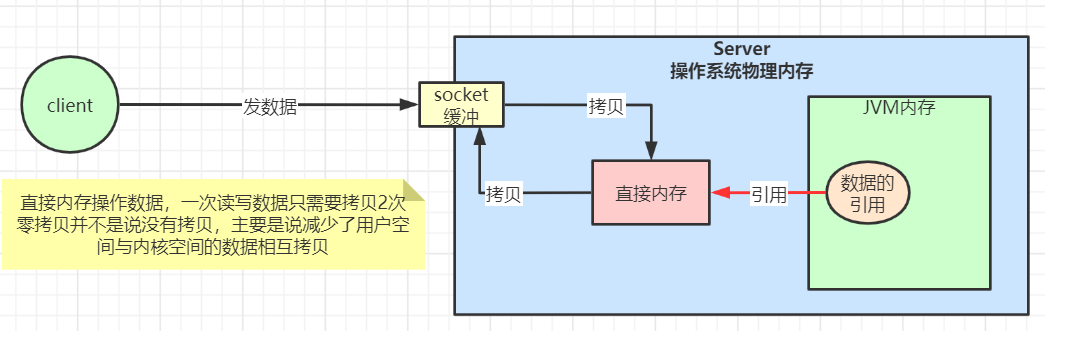
阿里面试: RocketMQ如何实现每秒上十万QPS的超高吞吐量读取的?
这玩意儿表面看上去挺牛逼,但其实背后的逻辑和套路,在咱们开发里见过的那些招数,都能找到影子。 今天小北和大家一起系统化的梳理梳理一遍,让大家功力猛增,吊打面试官。 1. 消息存储:巧妙利用顺序写 先说…...

web:js原型污染简单解释
1. 什么是对象? 在 JavaScript 中,对象是一种包含属性和方法的数据结构。你可以把对象想象成一个存储键值对的容器。每个键(key)都有一个对应的值(value),这个值可以是数据或者函数。 let per…...

【C++打怪之路Lv7】-- 模板初阶
🌈 个人主页:白子寰 🔥 分类专栏:C打怪之路,python从入门到精通,数据结构,C语言,C语言题集👈 希望得到您的订阅和支持~ 💡 坚持创作博文(平均质量分82)&#…...

实战OpenCV之模板匹配
基础入门 模板匹配是计算机视觉中一种常用的图像处理技术,用于在较大的目标图像中寻找与给定模板图像相似的子区域。这项技术的基本思想是在主图像中寻找与模板图像最相似的子区域,广泛应用于目标检测、图像识别等领域。模板匹配的主要流程包括如下三点。 1、滑动窗口。将模板…...

【C++ 11】for 基于范围的循环
文章目录 【 1. 基本用法 】【 2. for 新格式的应用 】2.1 for 遍历字符串2.2 for 遍历列表2.3 for 遍历的同时修改元素 问题背景 C 11标准之前(C 98/03 标准),如果要用 for 循环语句遍历一个数组或者容器,只能套用如下结构&#…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
