基于主成分分析的混音方法
一、简介:
基于主成分分析的混音方法是一种常见的音频混音技术,它利用主成分分析(PCA)对音频信号进行降维和重构,从而实现混音。
二、基本步骤如下:
采集和存储需要混音的音频信号。
对音频信号进行主成分分析,提取出主成分,即数据中最主要的信息。
将主成分进行降维处理,只保留其中的一部分信息。
将不同音频信号的降维主成分按照一定比例加权叠加,得到混音后的主成分。
将混合后的主成分重构为混音后的音频信号。
三、有优缺点分析:
基于主成分分析的混音方法的优点在于,它可以自动地提取数据中最主要的信息,并将其用于混音,从而降低混音的复杂度。此外,该方法还可以处理高维数据,因此可以用于多个信号的混音。
四、下面是一个基于主成分分析的混音方法的示例代码,在该示例代码中,我们使用了一个名为eigen_decomposition()的函数来执行协方差矩阵的特征值分解。实际上,该函数需要根据具体情况进行实现。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N 1024 // number of samples
#define M 2 // number of audio signals
#define K 1 // number of mixed components
float x[N][M]; // audio signals
float z[N][K]; // mixed components
float w[M][K]; // mixing weights
float y[N][M]; // mixed audio signals
void pca_mixing() {
int i, j, k;
float sum_x, sum_w, sum_y;
// calculate mean of audio signals
float mean[M];
for (j = 0; j < M; j++) {
sum_x = 0.0;
for (i = 0; i < N; i++) {
sum_x += x[i][j];
}
mean[j] = sum_x / N;
}
// subtract mean from audio signals
for (j = 0; j < M; j++) {
for (i = 0; i < N; i++) {
x[i][j] -= mean[j];
}
}
// calculate covariance matrix of audio signals
float cov[M][M];
for (j = 0; j < M; j++) {
for (k = 0; k < M; k++) {
sum_w = 0.0;
for (i = 0; i < N; i++) {
sum_w += x[i][j] * x[i][k];
}
cov[j][k] = sum_w / (N - 1);
}
}
// peform eigenvalue decomposition of covariance matrix
float eigval[M];
float eigvec[M][M];
eigen_decomposition(cov, eigval, eigvec);
/ select top K eigenvectors
float top_eigvec[M][K];
for (j = 0; j < K; j++) {
for (k = 0; k < M; k++) {
top_eigvec[k][j] = eigvec[k][M-j-1];
}
}
// calculate mixing weights
for (j = 0; j < M; j++) {
for (k = 0; k < K; k++) {
sum_w = 0.0;
for (i = 0; i < M; i++) {
sum_w += top_eigvec[i][k] * cov[i][j];
}
w[j][k] = sum_w / eigval[k];
}
}
// calculate mixed components
for (k = 0; k < K; k++) {
for (i = 0; i < N; i++) {
sum_x = 0.0;
for (j = 0; j < M; j++) {
sum_x += w[j][k] * x[i][j];
}
z[i][k] = sum_x;
}
}
// calculate mixed audio signals
for (j = 0; j < M; j++) {
for (i = 0; i < N; i++) {
sum_y = 0.0;
for (k = 0; k < K; k++) {
sum_y += w[j][k] * z[i][k];
}
y[i][j] = sum_y;
}
}
}
相关文章:

基于主成分分析的混音方法
一、简介: 基于主成分分析的混音方法是一种常见的音频混音技术,它利用主成分分析(PCA)对音频信号进行降维和重构,从而实现混音。 二、基本步骤如下: 采集和存储需要混音的音频信号。 对音频信号进行主成分…...
Code Two Exchange Crack
CodeTwo Exchange 迁移允许直接从早期版本的 Exchange(从 Exchange 2010 开始)安全、轻松地迁移到 Exchange 2019 和 2016。此服务器应用程序还允许您集中管理来自 Microsoft 365 (Office 365) 的邮箱迁移以及来自基于 IMAP 的电子邮件系统(例…...

jQuery.form.js 详细用法_维护老项目使用
概述 jquery-3.3.1.min.js : http://jquery.com/download jquery.form.min.js :http://malsup.com/jquery/form/#tab7 jquery form 是一个表单异步提交的插件,可以很容易提交表单,设置表单提交的参数,并在表单提交前…...

【Java】关于你不知道的Java大整数运算之BigInteger类超级好用!!!
目录 一、BigInteger类简单介绍 二、BigInteger构造方式 (1)构造方式 (2)输入方式 三、BigInteger常见的成员方法 (1)方法介绍 (2)方法使用演示 1.加减乘除余 2.比较 3.绝…...
运维是不是没有出路了?
瑞典马工的《是时候让运维集体下岗了》一出,就让运维人为之一颤,人人自危。文章开篇就提到:明人不说暗话,在云原生和DevOps成熟的今天,运维作为一个岗位和团队已经完成了历史任务,应该退出舞台了…...
【C++笔试强训】第七天
选择题 解析:内联函数(inline)一般用于代码较少,代码块里面没有递归且频繁调用的函数,是一种以空间换时间(不是指内存,而是指令变多编译出来的可执行程序会变大)的做法。内联函数在预…...

mysql binlog 一直追加写,磁盘满了怎么办?
文章目录 mysql binlog 清理策略1、设置binlog最大的文件数和文件大小2、定时清理过期binlog文件3、手动清理binlog文件4、禁用或启用binlogmysql binlog用于记录mysql数据库所有变更(数据库的DDL、DML操作)包括用户执行的语句,以及底层引擎所执行的操作的二进制日志,主要用…...
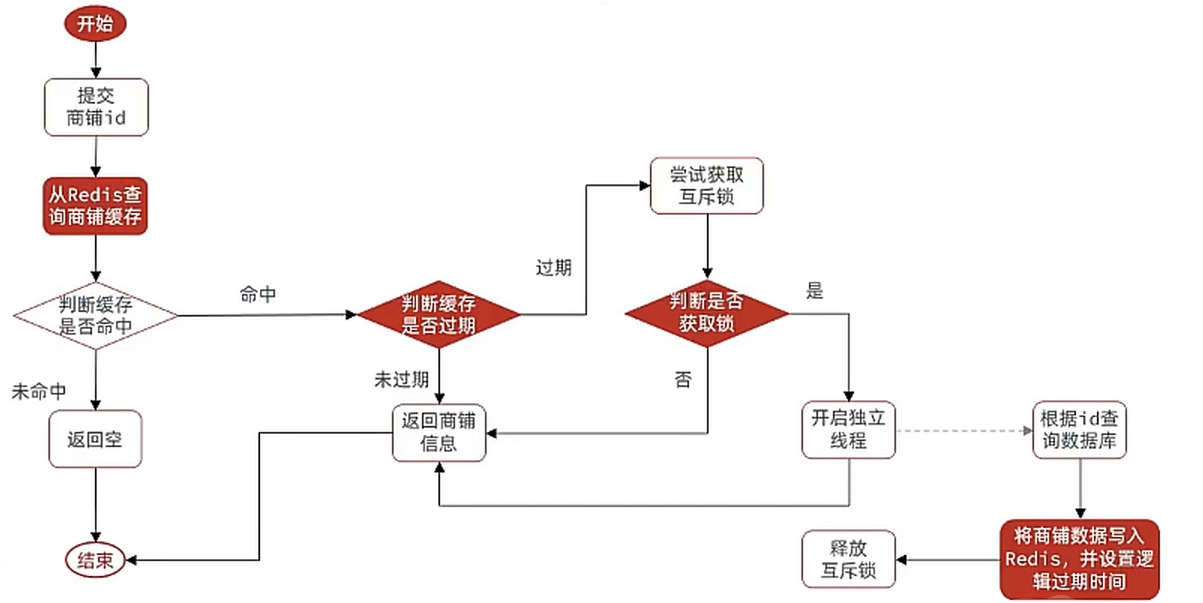
缓存穿透、缓存雪崩、缓存击穿解决方案
什么是缓存 缓存就是数据交换的缓冲区(称作Cache),是存贮数据的临时地方,一般读写性能较高。 添加 redis 缓存 给店铺类型查询业务添加缓存 需求:添加ShopTypeController中的queryTypeList方法,添加查询缓存 缓存更新…...
web + servlet + jdbc mysql 实现简单的表单管理界面
目录数据库创建数据库连接servlet创建,这里注意一下我的数据库我自己改了一下名字lhx网页html运行文件目录展示首先我们准备好开发使用的工具以及配置 idea2020 tomcat8.5 创建javaweb参考idea编译Tomcat详细步骤 IDEA通过JDBC连接数据库请参考jdbc连接数据库 需要登陆注册界面…...

Maven 国内镜像仓库
镜像仓库目标 当我们未定义任何远程仓库时,使用 Maven 更新依赖时,其会去默认远程仓库中拉取,默认远程仓库 是国外地址,所以在国内访问特别慢,想提升访问速度,需要将国外地址换成国内地址 更换仓库地址的…...

day21 ● 530.二叉搜索树的最小绝对差 ● 501.二叉搜索树中的众数 ● 236. 二叉树的最近公共祖先
二叉搜索树的最小绝对差 二叉搜索树(Binary Search Tree,简称 BST)是一种特殊的二叉树,它的每个节点都满足以下条件: 左子树上所有节点的值均小于该节点的值;右子树上所有节点的值均大于该节点的值&#…...
专业推荐竞赛 / 证书 官网及赛事相关信息整理)
大学计算机(软件类)专业推荐竞赛 / 证书 官网及赛事相关信息整理
大学计算机专业(软件)推荐竞赛 / 证书 官网及赛事相关信息 一、算法类(丰富简历): 1、ACM国际大学生程序设计竞赛: 官网:https://icpc.global/ 国内:http://icpc.pku.edu.cn/index.htm 报名方式:区域预赛一般每年9-1…...

Metasploit入门到高级【第九章】
预计更新第一章:Metasploit 简介 Metasploit 是什么Metasploit 的历史和发展Metasploit 的组成部分 第二章:Kali Linux 入门 Kali Linux 简介Kali Linux 安装和配置常用命令和工具介绍 第三章:Metasploit 基础 Metasploit 的基本概念Met…...

JDK之8后: 协程? 虚拟线程!!!
特性官方文档: https://openjdk.org/jeps/436 Java协程 近三十年来,Java 开发人员一直依赖线程作为并发服务器应用程序的构建块。每个方法中的每个语句都在线程内执行,并且由于 Java 是多线程的,因此多个执行线程同时发生。线程是Java的并发…...
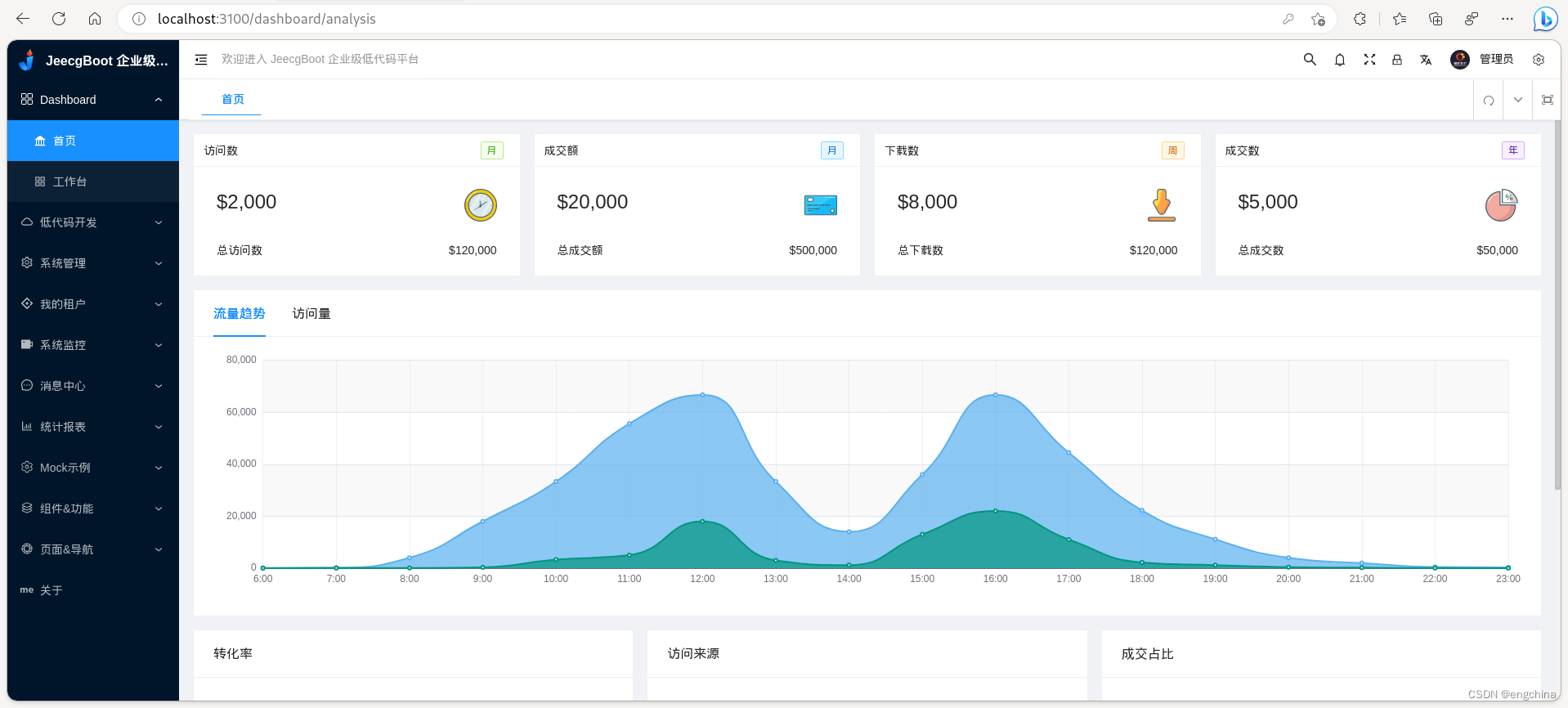
体验 jeecg
体验 jeecg官网地址事前准备安装升级 node 和 npm 版本验证安装安装 pnpm clidocker 启动 MySQLdocker 启动 redisgit clone 项目启动JAVA项目 jeecg-boot启动Vue3项目 jeecgboot-vue3官网地址 http://www.jeecg.com/ 事前准备 (1) 为了回避Could not find artifact com.mic…...
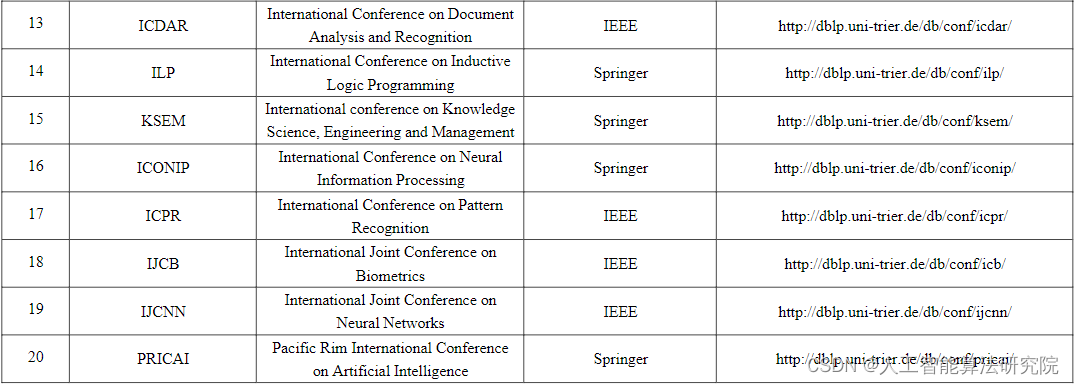
投稿指南【NO.13】计算机学会CCF推荐期刊和会议分享(人工智能)
前 言国内高等院校研究生及博士毕业条件需要发表高水平期刊或者顶会(清北上交等重点学校毕业要求为至少发一篇顶会),很多同学私信问到一级学会的会议论文怎么找、是什么,比如前段时间放榜的CVPR论文就是人工智能领域的顶会国际会议…...
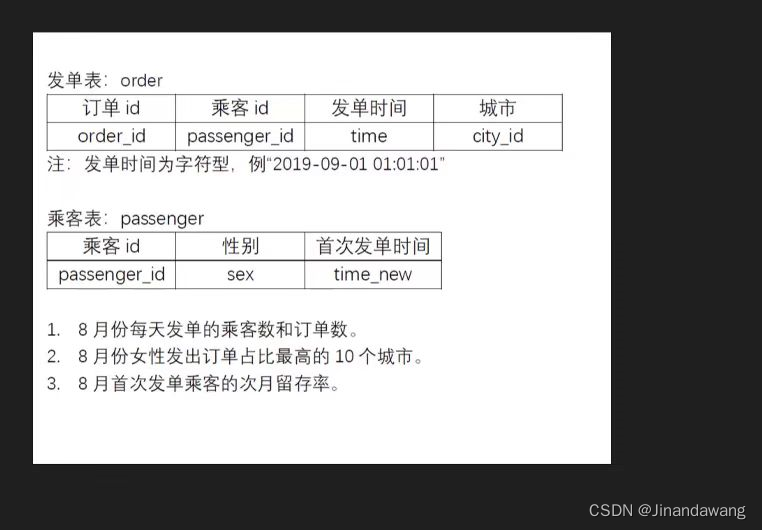
一份sql笔试
1、 select substr(time,1,10),count(order_id),count(distinct passenger_id) from order where substr(time,1,7)2023-08 group by substr(time,1,10) order by substr(time,1,10);2、 select city_id from (select * from order where substr(time,1,7) 2022-08) t1 left j…...

交换瓶子
交换瓶子 贡献者:programmer_ada 有N个瓶子,编号 1 ~ N,放在架子上。 比如有5个瓶子: 2 1 3 5 4 要求每次拿起2个瓶子,交换它们的位置。 经过若干次后,使得瓶子的序号为: 1 2 3 4 5 对于这么…...

二、Docker安装、启动、卸载、示例
Docker 支持 CentOS 6 及以后的版本,可以直接通过yum进行安装: 使用流程:启动主机 – 启动Docker服务 – 下载容器镜像 – 启动镜像得一个到容器 – 进入容器使用我们想要的程序 主机一般是Linux、Utuban 以下主机系统以CentOS7为例子&#…...

开心档之C++ STL 教程
C STL 教程 目录 C STL 教程 实例 在前面的章节中,我们已经学习了 C 模板的概念。C STL(标准模板库)是一套功能强大的 C 模板类,提供了通用的模板类和函数,这些模板类和函数可以实现多种流行和常用的算法和数据结构…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
