数据结构之红黑树的实现

1. 红⿊树的概念

红⿊树是⼀棵⼆叉搜索树，他的每个结点增加⼀个存储位来表⽰结点的颜⾊，可以是红⾊或者⿊⾊。通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束，红⿊树确保没有⼀条路径会⽐其他路径⻓出2倍，因⽽是接近平衡的

1.1 红⿊树的规则：

1. 每个结点不是红⾊就是⿊⾊
2. 根结点是⿊⾊的
3. 如果⼀个结点是红⾊的，则它的两个孩⼦结点必须是⿊⾊的，也就是说任意⼀条路径不会有连续的红⾊结点。
4. 对于任意⼀个结点，从该结点到其所有NULL结点的简单路径上，均包含相同数量的⿊⾊结点说明：《算法导论》等书籍上补充了⼀条每个叶⼦结点(NIL)都是⿊⾊的规则。他这⾥所指的叶⼦结点不是传统的意义上的叶⼦结点，⽽是我们说的空结点，有些书籍上也把NIL叫做外部结点。NIL是为了⽅便准确的标识出所有路径，《算法导论》在后续讲解实现的细节中也忽略了NIL结点，所以我们知道⼀下这个概念即可。

这棵树的路径数为9.

引入NIL可以有效防止我们数错路径数

1.2 思考⼀下，红⿊树如何确保最⻓路径不超过最短路径的2倍的？

• 由规则4可知，从根到NULL结点的每条路径都有相同数量的⿊⾊结点，所以极端场景下，最短路径就就是全是⿊⾊结点的路径，假设最短路径⻓度为bh(black height)。
• 由规则2和规则3可知，任意⼀条路径不会有连续的红⾊结点，所以极端场景下，最⻓的路径就是⼀⿊⼀红间隔组成，那么最⻓路径的⻓度为2bh。
• 综合红⿊树的4点规则⽽⾔，理论上的全⿊最短路径和⼀⿊⼀红的最⻓路径并不是在每棵红⿊树都存在的。假设任意⼀条从根到NULL结点路径的⻓度为x，那么bh <= h <= 2bh。

1.3 红⿊树的效率：

假设N是红⿊树树中结点数量，h最短路径的⻓度，那么 2 −, 由此推出。h 1 <= N < 2 −2∗h 1
h ≈ logN ，也就是意味着红⿊树增删查改最坏也就是⾛最⻓路径 2 ∗ logN ，那么时间复杂度还是O(logN)红⿊树的表达相对AVL树要抽象⼀些，AVL树通过⾼度差直观的控制了平衡。红⿊树通过4条规则的颜⾊约束，间接的实现了近似平衡，他们效率都是同⼀档次，但是相对⽽⾔，插⼊相同数量的结点，红⿊树的旋转次数是更少的，因为他对平衡的控制没那么严格。

2. 红⿊树的实现

2.1 红⿊树的结构

// 枚举值表⽰颜⾊
enum Colour
{RED,BLACK
};
// 这⾥我们默认按key/value结构实现
template<class K, class V>
struct RBTreeNode
{
// 这⾥更新控制平衡也要加⼊parent指针pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{}
};
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:private:Node* _root = nullptr;
};

这一块的结构是跟AVL树是一样的，只是这里少了平衡因子，多了一个color

2.2 红⿊树的插⼊

2.2.1 红⿊树树插⼊⼀个值的⼤概过程

1. 插⼊⼀个值按⼆叉搜索树规则进⾏插⼊，插⼊后我们只需要观察是否符合红⿊树的4条规则。
2. 如果是空树插⼊，新增结点是⿊⾊结点。如果是⾮空树插⼊，新增结点必须红⾊结点，因为⾮空树插⼊，新增⿊⾊结点就破坏了规则4，规则4是很难维护的。
3. ⾮空树插⼊后，新增结点必须红⾊结点，如果⽗亲结点是⿊⾊的，则没有违反任何规则，插⼊结束
4. ⾮空树插⼊后，新增结点必须红⾊结点，如果⽗亲结点是红⾊的，则违反规则3。进⼀步分析，c是红⾊，p为红，g必为⿊，这三个颜⾊都固定了，关键的变化看u的情况，需要根据u分为以下⼏种情况分别处理。

说明：下图中假设我们把新增结点标识为c (cur)，c的⽗亲标识为p(parent)，p的⽗亲标识为
g(grandfather)，p的兄弟标识为u（uncle）。

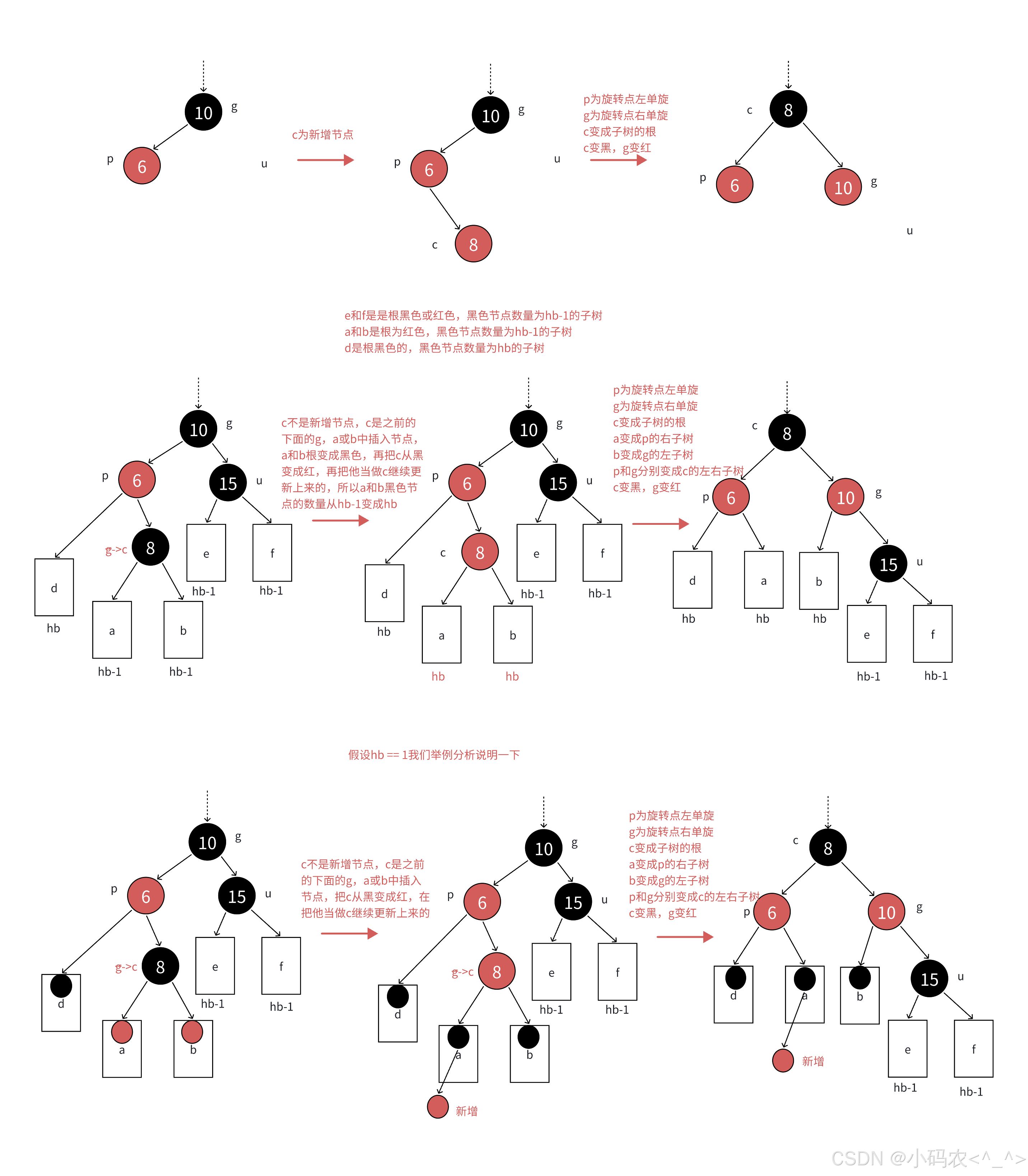
2.2.2 情况1：变⾊

c为红，p为红，g为⿊，u存在且为红，则将p和u变⿊，g变红。在把g当做新的c，继续往上更新。分析：因为p和u都是红⾊，g是⿊⾊，把p和u变⿊，左边⼦树路径各增加⼀个⿊⾊结点，g再变红，相当于保持g所在⼦树的⿊⾊结点的数量不变，同时解决了c和p连续红⾊结点的问题，需要继续往上更新是因为，g是红⾊，如果g的⽗亲还是红⾊，那么就还需要继续处理；如果g的⽗亲是⿊⾊，则处理结束了；如果g就是整棵树的根，再把g变回⿊⾊。情况1只变⾊，不旋转。所以⽆论c是p的左还是右，p是g的左还是右，都是上⾯的变⾊处理⽅式。

2.2.3 情况2：单旋+变⾊

c为红，p为红，g为⿊，u不存在或者u存在且为⿊，u不存在，则c⼀定是新增结点，u存在且为⿊，则c⼀定不是新增，c之前是⿊⾊的，是在c的⼦树中插⼊，符合情况1，变⾊将c从⿊⾊变成红⾊，更新上来的。
分析：p必须变⿊，才能解决，连续红⾊结点的问题，u不存在或者是⿊⾊的，这⾥单纯的变⾊⽆法解决问题，需要旋转+变⾊。
g
p u
c
如果p是g的左，c是p的左，那么以g为旋转点进⾏右单旋，再把p变⿊，g变红即可。p变成课这颗树新的根，这样⼦树⿊⾊结点的数量不变，没有连续的红⾊结点了，且不需要往上更新，因为p的⽗亲是⿊⾊还是红⾊或者空都不违反规则。
g
u p
c
如果p是g的右，c是p的右，那么以g为旋转点进⾏左单旋，再把p变⿊，g变红即可。p变成课这颗树新的根，这样⼦树⿊⾊结点的数量不变，没有连续的红⾊结点了，且不需要往上更新，因为p的⽗亲是⿊⾊还是红⾊或者空都不违反规则。

2.2.4 情况2：双旋+变⾊

c为红，p为红，g为⿊，u不存在或者u存在且为⿊，u不存在，则c⼀定是新增结点，u存在且为⿊，则c⼀定不是新增，c之前是⿊⾊的，是在c的⼦树中插⼊，符合情况1，变⾊将c从⿊⾊变成红⾊，更新上来的。
分析：p必须变⿊，才能解决，连续红⾊结点的问题，u不存在或者是⿊⾊的，这⾥单纯的变⾊⽆法解决问题，需要旋转+变⾊。
g
p u
c

如果p是g的左，c是p的右，那么先以p为旋转点进⾏左单旋，再以g为旋转点进⾏右单旋，再把c变⿊，g变红即可。c变成课这颗树新的根，这样⼦树⿊⾊结点的数量不变，没有连续的红⾊结点了，且不需要往上更新，因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。

2.3 红⿊树的插⼊代码实现

bool insert(const pair<k, v>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = Black;}//根节点Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到该插入的位置了cur = new Node(kv);cur->_parent = parent;if (cur->_kv.first < parent->_kv.first)parent->_left = cur;elseparent->_right = cur;//链接curwhile (parent && parent->_col == Red){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == Red)//叔叔节点存在并且为红色{//			g//		p       u//  c grandfather->_col = Red;parent->_col = Black;uncle->_col = Black;cur = grandfather;parent = cur->_parent;}else//叔叔节点不存在{//			g//		p      //  c if (cur == parent->_left){RotateR(grandfather);parent->_col = Black;grandfather->_col = Red;}else{//			g//		p      //			c RotateL(parent);RotateR(grandfather);cur->_col = Black;grandfather->_col = parent->_col = Red;}break;}}else//parent为grandfather的右边{Node* uncle = grandfather->_left;if (uncle && uncle->_col == Red){//			g//		u       p//			cgrandfather->_col = Red;parent->_col = uncle->_col = Black;cur = grandfather;parent = cur->_parent;}else//uncle为空{//			g//		       p//				  cif (cur == parent->_right){RotateL(grandfather);parent->_col = Black;grandfather->_col = Red;}else{//			g//		       p//			cRotateR(parent);RotateL(grandfather);grandfather->_col = Red;cur->_col = Black;}break;}}}_root->_col = Black;return true;
}

2.4 红⿊树的查找

Node* find(const pair<k,v>& kv)
{Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){cur = cur->_right;}else if (kv.first < cur->_kv.first){cur = cur->_left;}elsereturn cur;}return nullptr;
}

3 红⿊树的验证

这⾥获取最⻓路径和最短路径，检查最⻓路径不超过最短路径的2倍是不可⾏的，因为就算满⾜这个条件，红⿊树也可能颜⾊不满⾜规则，当前暂时没出问题，后续继续插⼊还是会出问题的。所以我们还是去检查4点规则，满⾜这4点规则，⼀定能保证最⻓路径不超过最短路径的2倍。

1. 规则1枚举颜⾊类型，天然实现保证了颜⾊不是⿊⾊就是红⾊。
2. 规则2直接检查根即可
3. 规则3前序遍历检查，遇到红⾊结点查孩⼦不太⽅便，因为孩⼦有两个，且不⼀定存在，反过来检查⽗亲的颜⾊就⽅便多了。
4. 规则4前序遍历，遍历过程中⽤形参记录跟到当前结点的blackNum(⿊⾊结点数量)，前序遍历遇到⿊⾊结点就++blackNum，⾛到空就计算出了⼀条路径的⿊⾊结点数量。再任意⼀条路径⿊⾊结点数量作为参考值，依次⽐较即可。

bool Check(Node* root, int blackNum, const int refNum)
{if (root == nullptr){// 前序遍历⾛到空时，意味着⼀条路径⾛完了//cout << blackNum << endl;if (refNum != blackNum){cout << "存在⿊⾊结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩⼦不太⽅便，因为孩⼦有两个，且不⼀定存在，反过来检查⽗亲就⽅便多了if (root->_col == Red && root->_parent->_col == Red){cout << root->_kv.first << "存在连续的红色结点" << endl;return false;}if (root->_col == Black){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);
}
bool IsBalance()
{if (_root == nullptr)return true;if (_root->_col == Red)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == Black){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);
}

这一块的实现还是有价值的，我的建议是大家都理解一下

4 总的代码

#include<iostream>
using namespace std;enum Color
{Red,Black
};template<class k, class v>
struct RBTreeNode
{pair<k, v> _kv;RBTreeNode<k, v>* _left;RBTreeNode<k, v>* _right;RBTreeNode<k, v>* _parent;Color _col;RBTreeNode(const pair<k, v>& kv) :_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(Red){}
};template<class k, class v>
class RBTree
{typedef RBTreeNode<k, v> Node;
public:bool insert(const pair<k, v>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = Black;}//根节点Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到该插入的位置了cur = new Node(kv);cur->_parent = parent;if (cur->_kv.first < parent->_kv.first)parent->_left = cur;elseparent->_right = cur;//链接curwhile (parent && parent->_col == Red){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == Red)//叔叔节点存在并且为红色{//			g//		p       u//  c grandfather->_col = Red;parent->_col = Black;uncle->_col = Black;cur = grandfather;parent = cur->_parent;}else//叔叔节点不存在{//			g//		p      //  c if (cur == parent->_left){RotateR(grandfather);parent->_col = Black;grandfather->_col = Red;}else{//			g//		p      //			c RotateL(parent);RotateR(grandfather);cur->_col = Black;grandfather->_col = parent->_col = Red;}break;}}else//parent为grandfather的右边{Node* uncle = grandfather->_left;if (uncle && uncle->_col == Red){//			g//		u       p//			cgrandfather->_col = Red;parent->_col = uncle->_col = Black;cur = grandfather;parent = cur->_parent;}else//uncle为空{//			g//		       p//				  cif (cur == parent->_right){RotateL(grandfather);parent->_col = Black;grandfather->_col = Red;}else{//			g//		       p//			cRotateR(parent);RotateL(grandfather);grandfather->_col = Red;cur->_col = Black;}break;}}}_root->_col = Black;return true;}void RotateR(Node* parent)//右旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* pparent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subL;subL->_parent = pparent;}else{pparent->_right = subL;subL->_parent = pparent;}}}void RotateL(Node* parent)//左旋{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* pparent = parent->_parent;parent->_parent = subR;subR->_left = parent;if (pparent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;subR->_parent = pparent;}else{pparent->_right = subR;subR->_parent = pparent;}}}void inorder(){_inorder(_root);}Node* find(const pair<k,v>& kv){Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){cur = cur->_right;}else if (kv.first < cur->_kv.first){cur = cur->_left;}elsereturn cur;}return nullptr;}bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍历⾛到空时，意味着⼀条路径⾛完了//cout << blackNum << endl;if (refNum != blackNum){cout << "存在⿊⾊结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩⼦不太⽅便，因为孩⼦有两个，且不⼀定存在，反过来检查⽗亲就⽅便多了if (root->_col == Red && root->_parent->_col == Red){cout << root->_kv.first << "存在连续的红色结点" << endl;return false;}if (root->_col == Black){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == Red)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == Black){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}
private:void _inorder(Node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_kv.first << ' ' << root->_kv.second << endl;_inorder(root->_right);}Node* _root = nullptr;
};

左旋右旋完全跟AVL树一样，这里我就不在多讲了，如果还有问题大家可以看一下我前一篇博客《AVL的实现》

5 简单总结

红黑树相较于AVL树抽象许多，但实际代码实现并不复杂，所以这一块的难点在于理解插入的过程，而插入的过程与uncle节点紧密相关，如果想要学好红黑树，uncle使我们必须要掌握的。