深度学习 .exp()
在 MXNet 中,.exp() 是 ndarray 对象的方法,用于计算数组中每个元素的指数(e 的幂)。此方法适用于所有类型的 ndarray,并返回一个新的数组,其中每个元素都是相应输入元素的指数。
语法
ndarray.exp()参数
- 此方法不需要任何额外的参数。
返回值
- 返回一个新的
ndarray,其元素为输入数组中对应元素的指数值。
示例
python
import mxnet as mx# 创建一个 ndarray
arr = mx.nd.array([0, 1, 2, 3])# 计算每个元素的指数
exp_arr = arr.exp()print(exp_arr) # 输出: [ 1. 2.7182817 7.389056 20.085537 ]注意事项
.exp()方法不会修改原始数组,而是返回一个新数组。- 计算的结果将根据输入数据的类型进行转换,通常会返回浮点型数组。
应用场景
- 在深度学习中,
exp()方法常用于激活函数(如 softmax 函数)以及概率计算等场景。
相关文章:
)
深度学习 .exp()
在 MXNet 中,.exp() 是 ndarray 对象的方法,用于计算数组中每个元素的指数(e 的幂)。此方法适用于所有类型的 ndarray,并返回一个新的数组,其中每个元素都是相应输入元素的指数。 语法 ndarray.exp() 参…...

从数据管理到功能优化:Vue+TS 项目实用技巧分享
引言 在项目开发过程中,优化用户界面和完善数据处理逻辑是提升用户体验的重要环节。本篇文章将带你一步步实现从修改项目图标、添加数据、优化日期显示,到新增自定义字段、调整按钮样式以及自定义按钮跳转等功能。这些操作不仅提升了项目的可视化效果&am…...
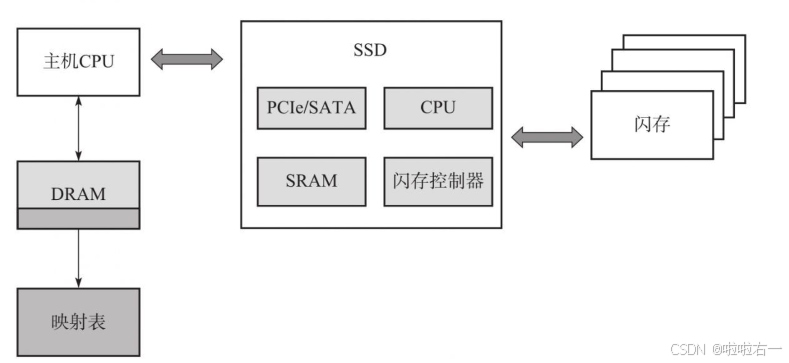
SSD |(六)FTL详解(上)
文章目录 📚FTL综述📚映射管理🐇映射的种类🐇映射的基本原理🐇HMB🐇映射表写入 📚FTL综述 当SSD所使用的主控和闪存确定后,FTL算法的好坏将直接决定SSD在性能、可靠性、耐用性等方面…...

程序报错:ModuleNotFoundError: No module named ‘code.utils‘; ‘code‘ is not a package
程序报错内容: Traceback (most recent call last): File "code/nli_inference/veracity_prediction.py", line 10, in <module> from code.utils.data_loader import read_json ModuleNotFoundError: No module named code.utils; code is …...

【closerAI ComfyUI】电商模特一键换装解决方案来了!细节到位无瑕疵!再加上flux模型加持,这个工作流不服不行!
不得了了兄弟们。这应该是电商界的福音,电商模特一键换装解决方案来了!细节到位无瑕疵!再加上flux模型加持,这个工作流不服不行! 这期我们主要讨论如何使用stable diffusion comfyUI 制作完美无瑕疵的换装工作流。** …...

【优选算法篇】编织算法的流动诗篇:滑动窗口的轻盈之美
文章目录 C 滑动窗口详解:基础题解与思维分析前言第一章:热身练习1.1 长度最小的子数组解法一(暴力求解)解法二(滑动窗口)滑动窗口的核心思想图解分析滑动窗口的有效性时间复杂度分析易错点提示 1.2 无重复…...
)
Linux 常用打包和压缩格式命令(tar tar.gz tar.bz2 tar.xz zip)
Linux 常用打包和压缩格式命令(tar tar.gz tar.bz2 tar.xz zip) 常用压缩包: tar 仅打包,不压缩。 gzip 使用DEFLATE算法进行压缩,通常用于.gz或.tar.gz文件。 bzip2 使用Burrows-Wheeler算法进行压缩,通常用于.bz2或.tar.bz2文件…...

Scala入门基础(12)抽象类
抽象类,制定标准,不要求去具体实现 包含了抽象方法的类就是抽象类。抽象方法只是有方法名,没有具体方法体的方法 定义抽象类要用abstract(抽象)关键字 用智能驾驶技术举例:演示)…...

unity静态批处理
unity静态批处理 静态批处理要求和兼容性渲染管线兼容性 使用静态批处理在构建时进行静态批处理在构建时执行静态批处理的步骤: 在运行时进行静态批处理性能影响 静态批处理 静态批处理是一种绘制调用批处理方法,它将不移动的网格组合在一起,…...

python项目实战——下载美女图片
python项目实战——下载美女图片 文章目录 python项目实战——下载美女图片完整代码思路整理实现过程使用xpath语法找图片的链接检查链接是否正确下载图片创建文件夹获取一组图片的链接获取页数 获取目录页的链接 完善代码注意事项 完整代码 import requests import re import…...

git分布式版本控制系统命令介绍、功能作用案例、子模块等知识点总结
Git是一个分布式版本控制系统,广泛用于软件开发中。以下是Git的常用命令、功能、作用以及一些使用案例的详细介绍。 Git 基本命令 配置 git config: 配置用户信息,如用户名和电子邮件。 git config --global user.name "Your Name"git confi…...

第八课:Python学习之循环
循环 目标 程序的三大流程while 循环基本使用break 和 continuewhile 循环嵌套 01. 程序的三大流程 在程序开发中,一共有三种流程方式: 顺序 —— 从上向下,顺序执行代码分支 —— 根据条件判断,决定执行代码的 分支循环 —— …...
)
设计模式——建造者模式(5)
一、写在前面 创建型模式 单例模式工厂方法模式抽象工厂模式原型模式建造者模式 结构型模式行为型模式 二、介绍 建造者模式主要在以下场景中得到应用: 当需要创建的对象具有复杂的内部结构,且包含多个属性时,建造者模式可以将对象的构建…...

java面向对象编程--高级(二)
目录 一、内部类 1.1 成员内部类 1.1.1 静态和非静态 1.1.2 调用外部类的结构 1.2 局部内部类 1.2.1 非匿名和匿名 1.2.2 比较 1.2.3 练习 二、枚举类 2.1 枚举类讲解 2.2 代码实现 三、包装类 3.1 包装类与基本数据类型 3.2 练习 3.3 补充 四、自动生成单元测试…...

定时发送邮件
一、实验内容 在linux主机通过定时任务指定在每天12:12分定时发送邮件;邮件内容自定。 二、实验步骤 1.安装s-nali 2.编辑/etc/s-nail.rc 文件 3.配置文件 授权码获取:点击POP3/SMTP/IMAP,并且启用IMAP/SMTP服务 4、编辑任务定时器 三、…...

基于Java的免税商品优选购物商城设计与实现代码(论文+源码)_kaic
目 录 摘 要 Abstract 第一章 绪论 1.1 课题开发的背景 1.2 课题研究的意义 1.3 研究内容 第二章 系统开发关键技术 2.1 JAVA技术 2.2 MyEclipse开发环境 2.3 Tomcat服务器 2.4 Spring Boot框架 2.5 MySQL数据库 第三章 系统分析 3.1 系统可行性研究…...

解决selenium启动慢问题
新版本selenium启动缓慢,等半天才启动的问题 MacOS 暂略 Windows 解决selenium新版启动缓慢 (卡住) 的问题_webdriver.chrome()很慢-CSDN博客...

Springboot + zset + lua 实现滑动窗口
Component public class RedisRateLimiter {Autowiredprivate RedisTemplate<String, String> redisTemplate;private String luaScript() {return "redis.call(zremrangebyscore, KEYS[1], 0, tonumber(ARGV[1]) - tonumber(ARGV[2]) * 1000) " // 移除过期的…...

【深度学习】transformer为什么使用多头注意力极致?为什么不使用一个头
在现代深度学习中,Transformer 模型的多头注意力机制已被广泛应用,特别是在自然语言处理领域。最近我读到一篇有趣的博客文章,详细介绍了为什么 Transformer 采用多头注意力,而不是简单的单头注意力。文章从理论推导到代码实现,对多头注意力机制进行了深入分析。下面我为大…...

利用Excel数据合并到Word功能,官方名为“Word邮件合并”
### 利用Excel数据合并到Word功能,官方名为“Word邮件合并”简介 #### 引言 在日常办公场景中,我们经常需要将Excel中的数据批量插入到Word文档中,比如制作员工工资条、邀请函或是客户信息表等。传统的手工操作不仅耗时耗力,还容易…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
