Java基础系列-一文搞懂自定义排序
java自定义排序
自定义排序的理解:
我们首先看需求:一个二维数组
[[1,3],[8,10],[15,18],[2,6]]
我们的需求是根据集合(二维数组取出来的数据)
左边小的左边这种方式排序
例如1<8 排序方式就是[1,3],[8,10]
此时我们就需要自定义排序
intervals={{1,3},{8,10},{15,18},{2,6}};Arrays.sort(intervals,new Comparator<int[]>(){public int compare(int[]s1,int []s2){return s1[0]-s2[0];}})
这段代码这样理解 comparator是比较器 是一个接口
我们使用匿名内部类方法 new 一个比较器 这时候必须实现里面的方法 compare方法返回值是Int
我们需要比较的对象是数组 根据数组左边的元素大小来排序
这时候参数就是int[]s1,int[]s2
实现compare方法
如果s1比s2大 返回就是1 那么 s1就排在后面
我们需要记住备操作的永远是第一个传参进来的数
例如我们在compare里面写
public int compare(int[]s1,int []s2){return s2[0]-s1[0];}
此时如果s1大于s2返回值是 负一 那么s1就会排在前面
这一点理解非常重要
如果不熟悉匿名内部类的同学
也可以自定义类实现Comparator接口的compare方法
然后传参给Arrays.sort的第二个参数
例如
class mycomparator implements Comparator<int[]>
{
public int compare()
{
定义你要实现比较的方法;
}}Arrays.sort(需要排序的数据,new mycomparator());
//就可以啦
还有一点就是多重数组可能给大家搞混 永远记住
[][] [][]这类【】【】的从外到内的数字 也是数组从外到内的过程。
例如
arr[1][0];//二位数组里面第二个数组的第一个数字
相关文章:

Java基础系列-一文搞懂自定义排序
java自定义排序 自定义排序的理解: 我们首先看需求:一个二维数组 [[1,3],[8,10],[15,18],[2,6]] 我们的需求是根据集合(二维数组取出来的数据) 左边小的左边这种方式排序 例如1<8 排序方式就是[1,3],[8,10] 此时我们就需…...

扫普通链接二维码打开小程序
1. 2.新增规则(注意下载文件到跟目录下,需要建个文件夹放下载的校验文件) 3.发布 ps:发布后,只能访问正式版本。体验版本如果加了 测试链接http://xxx/xsc/10 那么http://xxx/xsc/aa.....应该都能访问 例如aa101 aa…...

计算机储存与分区
Disk partitioning 盘分区是在辅助储存上创建一个或多个区域,以便可以单独管理每个区域。而这些区域称为分区(partition)。这通常是在为新盘选择分区方案后,需要做的事。 MBR and GPT 分区方案(分区表)有…...

OpenCV之换脸技术:一场面部识别的奇妙之旅
在这个数字化与智能化并进的时代,图像处理技术日益成为连接现实与虚拟世界的桥梁。其中,换脸技术作为一项颇受欢迎且富有挑战性的应用,不仅让人惊叹于技术的魔力,更在娱乐、影视制作等领域展现了无限可能。今天,我们就…...

Linux学习笔记9 文件系统的基础
一、查看文件组织结构 Linux中一切都是文件。 Linux和Win的文件系统不是一个结构,Linux存在的根目录是所有目录的起点。 所有的存储空间和设备共享一个根目录,不同的磁盘块和分区挂载在其下,成为某个子目录的子目录,甚至设备也挂…...
Android OpenGL粒子特效
在本篇,我们将开启一个新的项目,探索粒子的世界。粒子是一种基本的图形元素,它们通常被表示为一组点。通过巧妙地组合一些基础的物理效果,我们能够创造出许多令人惊叹的视觉效果。想象一下,我们可以模拟一个水滴从喷泉…...

5 -《本地部署开源大模型》在Ubuntu 22.04系统下ChatGLM3-6B高效微调实战
在Ubuntu 22.04系统下ChatGLM3-6B高效微调实战 无论是在单机单卡(一台机器上只有一块GPU)还是单机多卡(一台机器上有多块GPU)的硬件配置上启动ChatGLM3-6B模型,其前置环境配置和项目文件是相同的。如果大家对配置过程还…...
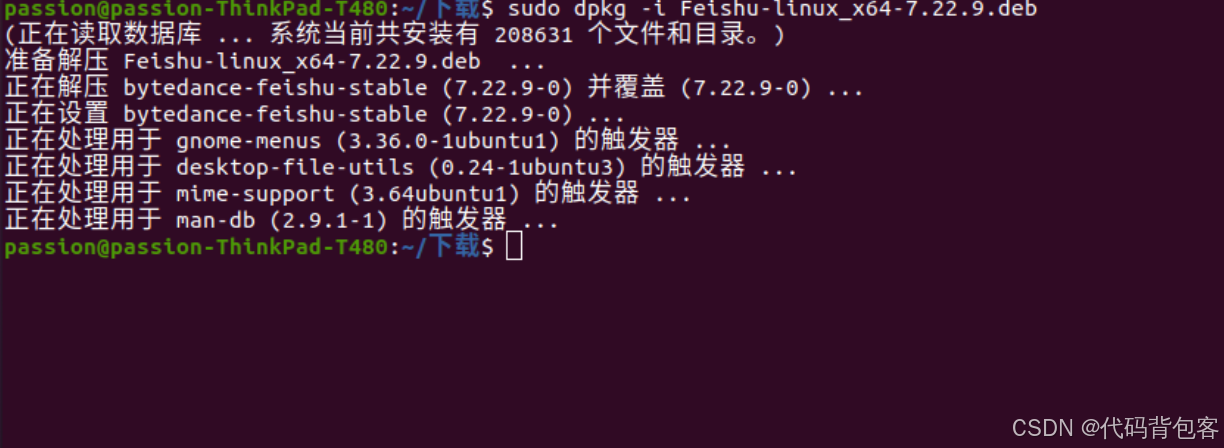
dpkg:错误:另外一个进程已经为dpkg前端锁加锁
一、 问题描述 在新装ubuntu系统时,我们常常会遇见dpkg的错误,dpkg:错误:另外一个进程已经为dpkg前端锁加锁,如下图。 二、问题解决 方法一 先执行sudo rm /var/lib/dpkg/lock-frontend然后再继续安装软件包,如果出现问题dpkg:…...
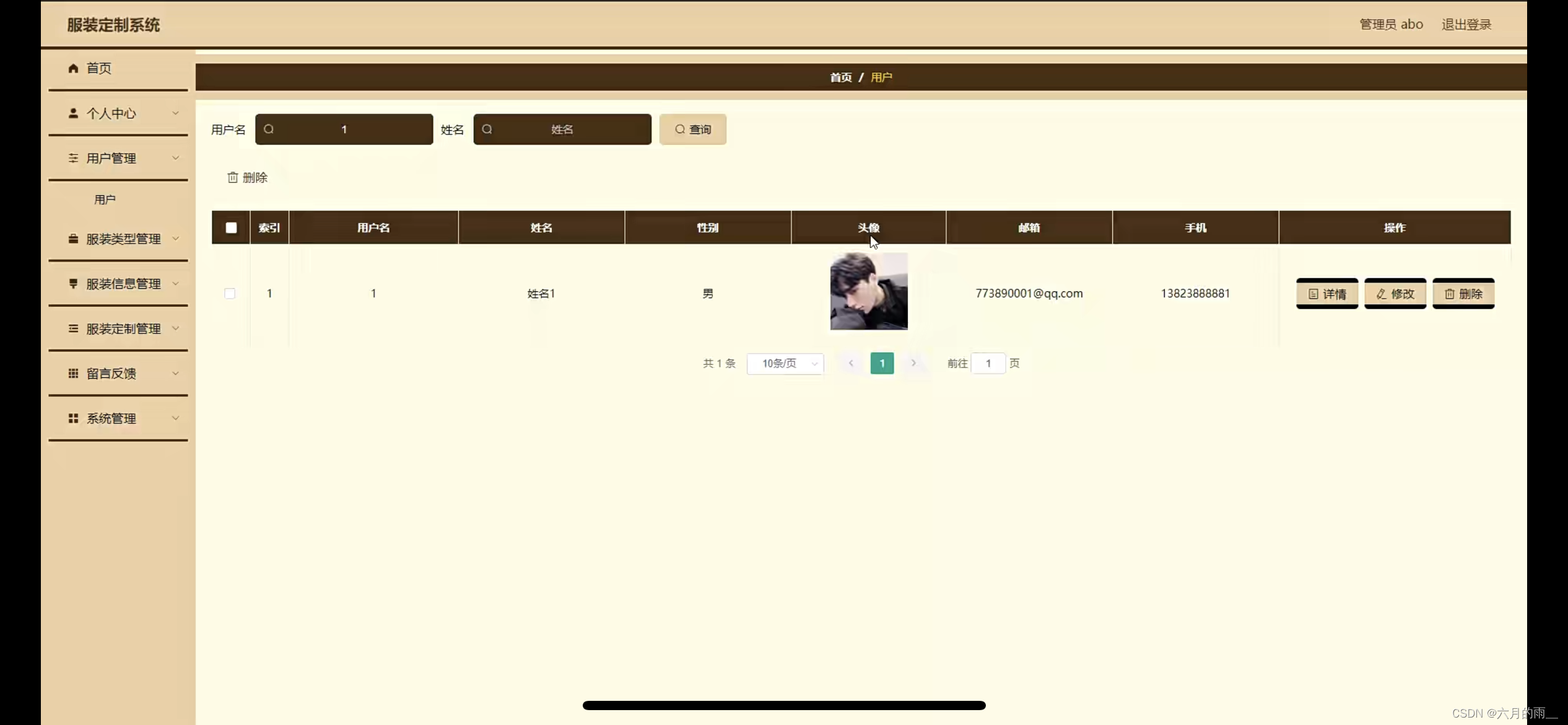
基于SSM服装定制系统的设计
管理员账户功能包括:系统首页,个人中心,用户管理,服装类型管理,服装信息管理,服装定制管理,留言反馈,系统管理 前台账号功能包括:系统首页,个人中心…...

RK3588开发笔记-usb3.0 xhci-hcd控制器挂死问题解决
目录 前言 一、问题现象 二、问题分析 三、问题排查 总结 前言 在使用 RK3588 芯片进行开发的过程中,我遇到了 USB 3.0 xHCI-HCD 控制器外接5G通讯模块偶尔挂死的问题。这个问题导致 USB 设备失去响应,且不能恢复,需要重启整个系统才能恢复使用,针对该问题进行大量测试以…...

深入解析TCP/IP协议:网络通信的基石
1. 引言 TCP/IP 协议是现代计算机网络的核心,它为互联网上的设备提供了通信的基础。在网络通信中,TCP/IP 协议栈是无处不在的,无论是个人设备的浏览器请求,还是大型分布式系统的内部通信,都依赖于它的稳定、高效与可靠…...

基于微信小程序的汽车预约维修系统(lw+演示+源码+运行)
基于微信小程序的汽车预约维修系统 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了基于微信小程序的汽车预约维修系统的开发全过程。通过分析基于微信小程序的汽车预约维修系统管理的不足,创建了…...
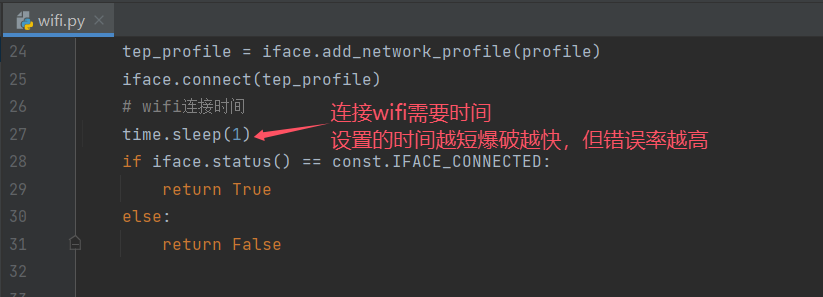
wifi、热点密码破解 - python
乐子脚本,有点小慢,试过多线程,系统 wifi 连接太慢了,需要时间确认,多线程的话系统根本反应不过来。 也就可以试试破解别人的热点,一般都是 123456 这样的傻鸟口令 # coding:utf-8 import pywifi from pyw…...
bean的实例化2024年10月17日
跟不上为基础 1.你的java学习路线 2. 3.课程 注解的装配 contoller调用service用的是注解装配...

告别ELK,APO提供基于ClickHouse开箱即用的高效日志方案——APO 0.6.0发布
ELK一直是日志领域的主流产品,但是ElasticSearch的成本很高,查询效果随着数据量的增加越来越慢。业界已经有很多公司,比如滴滴、B站、Uber、Cloudflare都已经使用ClickHose作为ElasticSearch的替代品,都取得了不错的效果ÿ…...
)
Excel使用技巧:定位Ctrl+G +公式+原位填充 Ctrl+Enter快速填充数据(处理合并单元格)
Excel的正确用法: Excel是个数据库,不要随意合并单元格。 数据输入的时候一定要按照行列输入,中间不要留空,不然就没有关联。 定位CtrlG 公式原位填充 CtrlEnter快速填充数据 如果把合并的单元格 取消合并,只有第一…...

JAVA学习-练习试用Java实现“成绩归类”
问题: 编写程序,输入一批学生的成绩,遇0或负数则输入结束,要求统计并输出优秀(大于85)、通过(60~84)和不及格(小于60)的学生人数。 示例 &#x…...
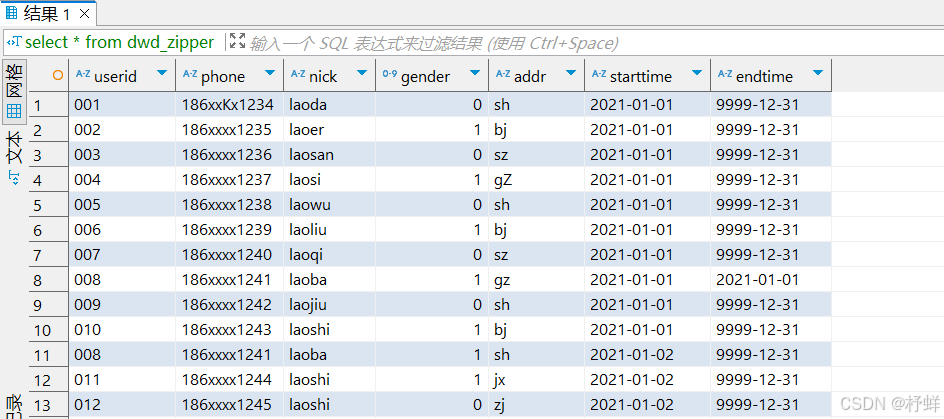
【Hive】7-拉链表的设计与实现
拉链表的设计与实现 数据同步问题 背景 例如:MySQL中有一张用户表: tb_user,每个用户注册完成以后,就会在用户表中新增该用户的信息,记录该用户的id、手机号码、用户名、性别、地址等信息。 每天都会有用户注册,产生…...

Maxwell 底层原理 详解
Maxwell 是一个 MySQL 数据库的增量数据捕获(CDC, Change Data Capture)工具,它通过读取 MySQL 的 binlog(Binary Log)来捕获数据变化,并将这些变化实时地发送到如 Kafka、Kinesis、RabbitMQ 或其他输出端。…...

使用短效IP池的优势是什么?
短效IP池作为代理IP服务中一种独特的资源管理方式,其应用已经在数据采集、市场分析和网络安全等多个领域中展示出强大的功能。尽管“短效”听起来似乎意味着某种限制,然而在某些特定的应用场景下,短效IP池却提供了无可比拟的优势。本文将详细…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
