【C++】红黑树万字详解(一文彻底搞懂红黑树的底层逻辑)
目录
00.引入
01.红黑树的性质
02.红黑树的定义
03.红黑树的插入
1.按照二叉搜索树的规则插入新节点
2.检测新节点插入后,是否满足红黑树的性质
1.uncle节点存在且为红色
2.uncle节点不存在
3.uncle节点存在且为黑色
04.验证红黑树
00.引入
和AVL树一样,红黑树也是一种自平衡的二叉搜索树。AVL树通过平衡因子调整子树的高度,确保树的高度差在 -1 到 1 之间。而红黑树通过在每个节点上增加一个存储位表示节点的颜色,可以是RED或BLACK。通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有任何一条路径会是其他路径的两倍以上长,因而接近平衡。

01.红黑树的性质
红黑树具有以下几种性质,这些性质确保了树的平衡性和高效性:
1.节点颜色:每个节点要么是红色,要么是黑色。
2.根节点颜色:根节点始终是黑色。
3.红色节点限制:没有两个红色节点可以相连。
4.黑色节点数量:从任何节点到其每个叶子节点的所以路径包含相同数量的黑色节点。
5.叶子节点:所有的叶子节点(此处都表示为NULL节点)都是黑色。
其实还有一条潜规则:每一个新插入的节点初始都为红色。
为什么以上性质就可以保证最长路径的节点个数不会超过最短路径节点个数的两倍?
通过性质1/2/5可知,在判断性质4时(计算路径上黑色节点的数量),不需要考虑头节点以及叶子节点,只需要考虑中间节点即可,再根据性质3,可以列举以下几种情况:
1.中间没有黑色节点:
路径: 黑->黑,黑->红->黑。
2.中间只有1个黑色节点:
路径: 黑->黑->黑,黑->红->黑->黑,黑->黑->红->黑,黑->红->黑->红->黑
3.中间有2个黑色节点:
路径: 黑->黑->黑->黑,黑->红->黑->黑->黑,黑->黑->红->黑->黑,黑->黑->黑->红->黑
。。。黑->红->黑->红->黑->红->黑
可以看出,最短路径就是全黑的;最长路径是黑、红相间的。因而我们可以找到规律:
假设中间有n个黑色节点:
最短路径:n+2(中间节点加上首尾)
最长路径:n+(n+1)+2=2n+3(中间有n个黑色节点最多可以有n+1个红色节点)
所以最长路径(2n+3)永远比最短路径的2倍(2n+4)小1。
02.红黑树的定义
红黑树的底层结构在代码实现中使用节点结构体和数来表示。节点结构体 保存每个节点的数据、指向左右子节点、父节点的指针、以及平衡因子;树类管理插入、删除等操作。
// 节点的颜色
enum Color { RED, BLACK };// 红黑树节点的定义
template<class T>
struct RBTreeNode
{RBTreeNode(const T& data = T(), Color color = RED): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _color(color){}RBTreeNode<T>* _pLeft; // 节点的左孩子RBTreeNode<T>* _pRight; // 节点的右孩子RBTreeNode<T>* _pParent; // 节点的双亲T _data; // 节点的值域Color _color; // 节点的颜色
};
在节点的定义中,我们将节点默认颜色给成红色,这是因为如果定义成黑色的话,根据性质4,每一次插入节点都需要重新调整树,而定义成红色,就只需要在父节点也为红色时进行调整,一定程度上保证了插入的效率。
03.红黑树的插入
红黑树是在二叉搜索树的基础上加上平衡限制条件的,因此红黑树的插入可以分为两步:
1.按照二叉搜索树的规则插入新节点
// 在红黑树中插入值为data的节点,插入成功返回true,否则返回false// 注意:为了简单起见,本次实现红黑树不存储重复性元素bool Insert(const T& data){if (!_pRoot) // 根节点为空直接插入{_pRoot = new Node(data);_pRoot->_color = BLACK; // 设置根节点为黑色return true;}Node* pParent = nullptr;Node* pCur = _pRoot;while (pCur){pParent = pCur;if (data == pCur->_data) // 元素重复,不进行插入return false;else if (data > pCur->_data) // 大于向右走pCur = pCur->_pRight;else // 小于向左走pCur = pCur->_pLeft;}pCur = new Node(data);// 更新父节点的子节点指针if (data < pParent->_data)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;pCur->_pParent = pParent;return true;}二叉搜索树的插入过程不在赘述,详细可跳转这篇博客【C++】二叉搜索树。
2.检测新节点插入后,是否满足红黑树的性质
因为新插入节点默认为红色,因此如果双亲节点是黑色,则满足性质,不需要调整;如果双亲节点为红色,违反了性质3,需要进行调整,调整过程需要进行分类讨论:
第一种情况:
我们调整红黑树的底层逻辑是通过改变某些节点的颜色,使整棵树符合性质,看下面这棵树:

cur表示新插入节点,parent为父节点,grandpa为父节点的父节点,uncle为grandpa的另一个节点
(下面用c,p,g,u分别表示cur,parent,grandpa,uncle)
此时c和p是连续的红色节点。破坏了性质3,那么我直接把p的颜色改成黑色,性质3被修复,但同时又破坏了性质4,于是我把u的颜色也改成黑色,这样以g为根节点的这棵树确实被修复了。
 但要注意,如果g不是根节点呢
但要注意,如果g不是根节点呢
 此时性质4还是被破坏了,为此,把g的颜色改成红色
此时性质4还是被破坏了,为此,把g的颜色改成红色
 这样就完成了修复。但如果是下面这种情况呢
这样就完成了修复。但如果是下面这种情况呢
 g的双亲也为红色,此时需要继续向上调整。。
g的双亲也为红色,此时需要继续向上调整。。
所以我们得到了第一种情况:
1.uncle节点存在且为红色
a.祖父节点为根 或 祖父的双亲为黑色
只需要修改u和p的颜色即可

b.祖父节点不为根 且 祖父的双亲为红色
此时需要进一步向上调整

将cur的位置换到grandpa,p、u、g一并转换,此时u一定存在,如果u不存在,则违反了性质4
第二种情况:
2.uncle节点不存在
1.单旋的情况

学习过AVL树可以知道,对于这样的一棵树我们需要通过旋转的方法调整高度,关于旋转的原理,可以调整这篇博客【C++】AVL树
旋转完成之后,我们需要调整颜色,此时p成为了这棵树的根节点,为了满足条件4,我们把p颜色改成黑,g颜色改成红:

这是左单旋的情况,右单旋同理
2.双旋的情况

双旋分为 右左 与 左右 两种情况,右左即p是g的右孩子,c是p的左孩子。右左情况下我们需要对p进行右单旋,在对g进行左单旋,最后调整c和g的颜色,过程如下:

左右的情况同理
3.uncle节点存在且为黑色
a.单旋的情况

此时cur一定不是新插入节点,这种情况就是1.b向上调整的后续了,此时依旧要用到旋转操作,和情况2同理:

b.双旋的情况

由此看来,情况2和情况3其实可以合并。
下面给出插入以及旋转的完整代码:
template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree(){_pRoot = nullptr;}// 在红黑树中插入值为data的节点,插入成功返回true,否则返回false// 注意:为了简单起见,本次实现红黑树不存储重复性元素bool Insert(const T& data){if (!_pRoot) // 根节点为空直接插入{_pRoot = new Node(data);_pRoot->_color = BLACK; // 设置根节点为黑色return true;}Node* pParent = nullptr;Node* pCur = _pRoot;while (pCur){pParent = pCur;if (data == pCur->_data) // 元素重复,不进行插入return false;else if (data > pCur->_data) // 大于向右走pCur = pCur->_pRight;else // 小于向左走pCur = pCur->_pLeft;}pCur = new Node(data);// 更新父节点的子节点指针if (data < pParent->_data)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;pCur->_pParent = pParent;while (pParent && pParent->_color == RED){Node* pGrandpa = pParent->_pParent;if (!pGrandpa)pParent->_color = BLACK;else {if (pParent == pGrandpa->_pRight) {Node* pUncle = pGrandpa->_pLeft;// uncle存在且为红if (pUncle && pUncle->_color == RED){pUncle->_color = pParent->_color = BLACK;pGrandpa->_color = RED;// 继续向上调整pCur = pGrandpa;pParent = pCur->_pParent;}// uncle不存在或者uncle为黑else{// 右右的情况if (pCur == pParent->_pRight){RotateL(pGrandpa);pParent->_color = BLACK;pGrandpa->_color = RED;}// 右左的情况else{RotateR(pParent);RotateL(pGrandpa);pCur->_color = BLACK;pGrandpa->_color = RED;}break;}}else // pParent = pGrandpa->_pLeft{Node* pUncle = pGrandpa->_pRight;// uncle存在且为红if (pUncle && pUncle->_color == RED){pUncle->_color = pParent->_color = BLACK;pGrandpa->_color = RED;// 继续向上调整pCur = pGrandpa;pParent = pCur->_pParent;}// uncle不存在或者uncle为黑else{// 左左的情况if (pCur == pParent->_pLeft){RotateR(pGrandpa);pParent->_color = BLACK;pGrandpa->_color = RED;}// 左右的情况else{RotateL(pParent);RotateR(pGrandpa);pCur->_color = BLACK;pGrandpa->_color = RED;}break;}}}}_pRoot->_color = BLACK;return true;}private:// 左单旋void RotateL(Node* pParent){Node* pCur = pParent->_pRight;pParent->_pRight = pCur->_pLeft; // cur的左孩子作为parent的右孩子if (pCur->_pLeft)pCur->_pLeft->_pParent = pParent;if (pParent->_pParent) // parent不是根节点{pCur->_pParent = pParent->_pParent;if (pParent->_pParent->_pLeft == pParent)pParent->_pParent->_pLeft = pCur;elsepParent->_pParent->_pRight = pCur;}else // parent是根节点{_pRoot = pCur;pCur->_pParent = nullptr;}pParent->_pParent = pCur;pCur->_pLeft = pParent;}// 右单旋void RotateR(Node* pParent){Node* pCur = pParent->_pLeft;pParent->_pLeft = pCur->_pRight; // cur的右孩子作为parent的左孩子if (pCur->_pRight)pCur->_pRight->_pParent = pParent;if (pParent->_pParent) // parent不是根节点{pCur->_pParent = pParent->_pParent;if (pParent->_pParent->_pLeft == pParent)pParent->_pParent->_pLeft = pCur;elsepParent->_pParent->_pRight = pCur;}else // parent是根节点{_pRoot = pCur;pCur->_pParent = nullptr;}pParent->_pParent = pCur;pCur->_pRight = pParent;}private:Node* _pRoot;
};04.验证红黑树
检验上述代码,就得从红黑树的5条性质入手,性质1、5不需要验证,性质2也很容易验证,实际上我们主要验证的是性质3(没有连续的红色节点)以及性质4(每条路径上黑色节点数量一致)
对于性质4,我们可以先记录某一条路径(这里选取最左叶节点这条路径)的黑色节点数量,再遍历每一条路径,只要有一条路径上的黑色节点数量与前者不一样,就返回false,这里选择用递归的方式遍历红黑树。
对于性质3,我们需要再遍历的过程中,碰到红色节点,就验证一下双亲的颜色,如果也为红,则违反性质,返回false
完整代码如下:
// 检测红黑树是否为有效的红黑树,注意:其内部主要依靠_IsValidRBTRee函数检测bool IsValidRBTRee(){if (!_pRoot)return true;if (RED == _pRoot->_color)return false;Node* pCur = _pRoot;size_t blackcount = 0;while (pCur){if (BLACK == pCur->_color)++blackcount;pCur = pCur->_pLeft;}return _IsValidRBTRee(_pRoot, blackcount, 0);}bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t pathBlack) {if (!pRoot) {// 如果到达叶子节点,检查黑色节点数量return pathBlack == blackCount;}// 检查当前节点的颜色if (pRoot->_color == RED) {// 如果是红色,检查父节点是否也是红色if (pRoot->_pParent && pRoot->_pParent->_color == RED) {return false; // 违反红黑树性质}}// 更新路径上的黑色节点数量if (pRoot->_color == BLACK) {pathBlack++;}// 递归检查左子树和右子树return _IsValidRBTRee(pRoot->_pLeft, blackCount, pathBlack) &&_IsValidRBTRee(pRoot->_pRight, blackCount, pathBlack);}最后我们用一万组包含10个1~100随机数的数组验证红黑树:
#include<iostream>
using namespace std;
#include"My_RBTree.h"
#include<vector>bool test1()
{srand(time(0)); // 初始化随机种子// 生成10000组随机向量for (int i = 0; i < 10000; ++i) {RBTree<int> BT;vector<int> nums;// 每组随机生成10个整数(范围为 1 到 100)for (int j = 0; j < 10; ++j) {nums.push_back(rand() % 100 + 1);}// 将每个整数插入 B 树中for (const int& num : nums) {BT.Insert(num);}// 检查 B 树if (!BT.IsValidRBTRee()) {cout << "树不平衡,测试失败!\n";for (auto it : nums){cout << it << ", ";}cout << endl;return 1;}}cout << "所有10000组随机树均平衡,测试通过!\n";
}int main()
{test1();return 0;
}运行结果:

验证通过!
附上完整代码:
//My_RBTree.h
#pragma once
// 节点的颜色
enum Color { RED, BLACK };// 红黑树节点的定义
template<class T>
struct RBTreeNode
{RBTreeNode(const T& data = T(), Color color = RED): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _color(color){}RBTreeNode<T>* _pLeft; // 节点的左孩子RBTreeNode<T>* _pRight; // 节点的右孩子RBTreeNode<T>* _pParent; // 节点的双亲T _data; // 节点的值域Color _color; // 节点的颜色
};template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree(){_pRoot = nullptr;}// 在红黑树中插入值为data的节点,插入成功返回true,否则返回false// 注意:为了简单起见,本次实现红黑树不存储重复性元素bool Insert(const T& data){if (!_pRoot) // 根节点为空直接插入{_pRoot = new Node(data);_pRoot->_color = BLACK; // 设置根节点为黑色return true;}Node* pParent = nullptr;Node* pCur = _pRoot;while (pCur){pParent = pCur;if (data == pCur->_data) // 元素重复,不进行插入return false;else if (data > pCur->_data) // 大于向右走pCur = pCur->_pRight;else // 小于向左走pCur = pCur->_pLeft;}pCur = new Node(data);// 更新父节点的子节点指针if (data < pParent->_data)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;pCur->_pParent = pParent;while (pParent && pParent->_color == RED){Node* pGrandpa = pParent->_pParent;if (!pGrandpa)pParent->_color = BLACK;else {if (pParent == pGrandpa->_pRight) {Node* pUncle = pGrandpa->_pLeft;// uncle存在且为红if (pUncle && pUncle->_color == RED){pUncle->_color = pParent->_color = BLACK;pGrandpa->_color = RED;// 继续向上调整pCur = pGrandpa;pParent = pCur->_pParent;}// uncle不存在或者uncle为黑else{// 右右的情况if (pCur == pParent->_pRight){RotateL(pGrandpa);pParent->_color = BLACK;pGrandpa->_color = RED;}// 右左的情况else{RotateR(pParent);RotateL(pGrandpa);pCur->_color = BLACK;pGrandpa->_color = RED;}break;}}else // pParent = pGrandpa->_pLeft{Node* pUncle = pGrandpa->_pRight;// uncle存在且为红if (pUncle && pUncle->_color == RED){pUncle->_color = pParent->_color = BLACK;pGrandpa->_color = RED;// 继续向上调整pCur = pGrandpa;pParent = pCur->_pParent;}// uncle不存在或者uncle为黑else{// 左左的情况if (pCur == pParent->_pLeft){RotateR(pGrandpa);pParent->_color = BLACK;pGrandpa->_color = RED;}// 左右的情况else{RotateL(pParent);RotateR(pGrandpa);pCur->_color = BLACK;pGrandpa->_color = RED;}break;}}}}_pRoot->_color = BLACK;return true;}// 检测红黑树中是否存在值为data的节点,存在返回该节点的地址,否则返回nullptrNode* Find(const T& data){Node* pCur = _pRoot;while (pCur){if (data == pCur->_data)return pCur;if (data > pCur->_data)pCur = pCur->_pRight;elsepCur = pCur->_pLeft;}return nullptr;}// 检测红黑树是否为有效的红黑树,注意:其内部主要依靠_IsValidRBTRee函数检测bool IsValidRBTRee(){if (!_pRoot)return true;if (RED == _pRoot->_color)return false;Node* pCur = _pRoot;size_t blackcount = 0;while (pCur){if (BLACK == pCur->_color)++blackcount;pCur = pCur->_pLeft;}return _IsValidRBTRee(_pRoot, blackcount, 0);}private:bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t pathBlack) {if (!pRoot) {// 如果到达叶子节点,检查黑色节点数量return pathBlack == blackCount;}// 检查当前节点的颜色if (pRoot->_color == RED) {// 如果是红色,检查父节点是否也是红色if (pRoot->_pParent && pRoot->_pParent->_color == RED) {return false; // 违反红黑树性质}}// 更新路径上的黑色节点数量if (pRoot->_color == BLACK) {pathBlack++;}// 递归检查左子树和右子树return _IsValidRBTRee(pRoot->_pLeft, blackCount, pathBlack) &&_IsValidRBTRee(pRoot->_pRight, blackCount, pathBlack);}// 左单旋void RotateL(Node* pParent){Node* pCur = pParent->_pRight;pParent->_pRight = pCur->_pLeft; // cur的左孩子作为parent的右孩子if (pCur->_pLeft)pCur->_pLeft->_pParent = pParent;if (pParent->_pParent) // parent不是根节点{pCur->_pParent = pParent->_pParent;if (pParent->_pParent->_pLeft == pParent)pParent->_pParent->_pLeft = pCur;elsepParent->_pParent->_pRight = pCur;}else // parent是根节点{_pRoot = pCur;pCur->_pParent = nullptr;}pParent->_pParent = pCur;pCur->_pLeft = pParent;}// 右单旋void RotateR(Node* pParent){Node* pCur = pParent->_pLeft;pParent->_pLeft = pCur->_pRight; // cur的右孩子作为parent的左孩子if (pCur->_pRight)pCur->_pRight->_pParent = pParent;if (pParent->_pParent) // parent不是根节点{pCur->_pParent = pParent->_pParent;if (pParent->_pParent->_pLeft == pParent)pParent->_pParent->_pLeft = pCur;elsepParent->_pParent->_pRight = pCur;}else // parent是根节点{_pRoot = pCur;pCur->_pParent = nullptr;}pParent->_pParent = pCur;pCur->_pRight = pParent;}private:Node* _pRoot;
};//test.cpp
#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>using namespace std;#include"My_RBTree.h"#include<vector>bool test1(){srand(time(0)); // 初始化随机种子// 生成10000组随机向量for (int i = 0; i < 10000; ++i) {RBTree<int> BT;vector<int> nums;// 每组随机生成10个整数(范围为 1 到 100)for (int j = 0; j < 10; ++j) {nums.push_back(rand() % 100 + 1);}// 将每个整数插入 B 树中for (const int& num : nums) {BT.Insert(num);}// 检查 B 树if (!BT.IsValidRBTRee()) {cout << "树不平衡,测试失败!\n";for (auto it : nums){cout << it << ", ";}cout << endl;return 1;}}cout << "所有10000组随机树均平衡,测试通过!\n";}void test2(){RBTree<int> BT1;vector<int> v1 = { 70,25,97,18,51,85 };for (auto it : v1){BT1.Insert(it);}cout << BT1.IsValidRBTRee() << endl;}int main(){test1();return 0;}以上就是红黑树的详解与模拟实现过程,欢迎在评论区留言,码文不易,觉得这篇博客对你有帮助的,可以点赞收藏关注支持一波~😉
相关文章:

【C++】红黑树万字详解(一文彻底搞懂红黑树的底层逻辑)
目录 00.引入 01.红黑树的性质 02.红黑树的定义 03.红黑树的插入 1.按照二叉搜索树的规则插入新节点 2.检测新节点插入后,是否满足红黑树的性质 1.uncle节点存在且为红色 2.uncle节点不存在 3.uncle节点存在且为黑色 04.验证红黑树 00.引入 和AVL树一样&am…...

开源FluentFTP实操,操控FTP文件
概述:通过FluentFTP库,轻松在.NET中实现FTP功能。支持判断、创建、删除文件夹,判断文件是否存在,实现上传、下载和删除文件。简便而强大的FTP操作,提升文件传输效率。 在.NET中,使用FluentFTP库可以方便地…...

论文解读 | ECCV2024 AutoEval-Video:一个用于评估大型视觉-语言模型在开放式视频问答中的自动基准测试...
点击蓝字 关注我们 AI TIME欢迎每一位AI爱好者的加入! 点击 阅读原文 观看作者讲解回放! 作者简介 陈修元,上海交通大学清源研究院硕士生 概述 总结来说,我们提出了一个新颖且具有挑战性的基准测试AutoEvalVideo,用于全…...

postgresql14主从同步流复制搭建
1. 如果使用docker搭建请移步 Docker 启动 PostgreSQL 主从架构:实现数据同步的高效部署指南_docker安装postgresql主从同步-CSDN博客 2. 背景 pgsql版本:PostgreSQL 14.13 on x86_64-pc-linux-gnu, compiled by gcc (GCC) 4.8.5 20150623 (Red Hat 4…...
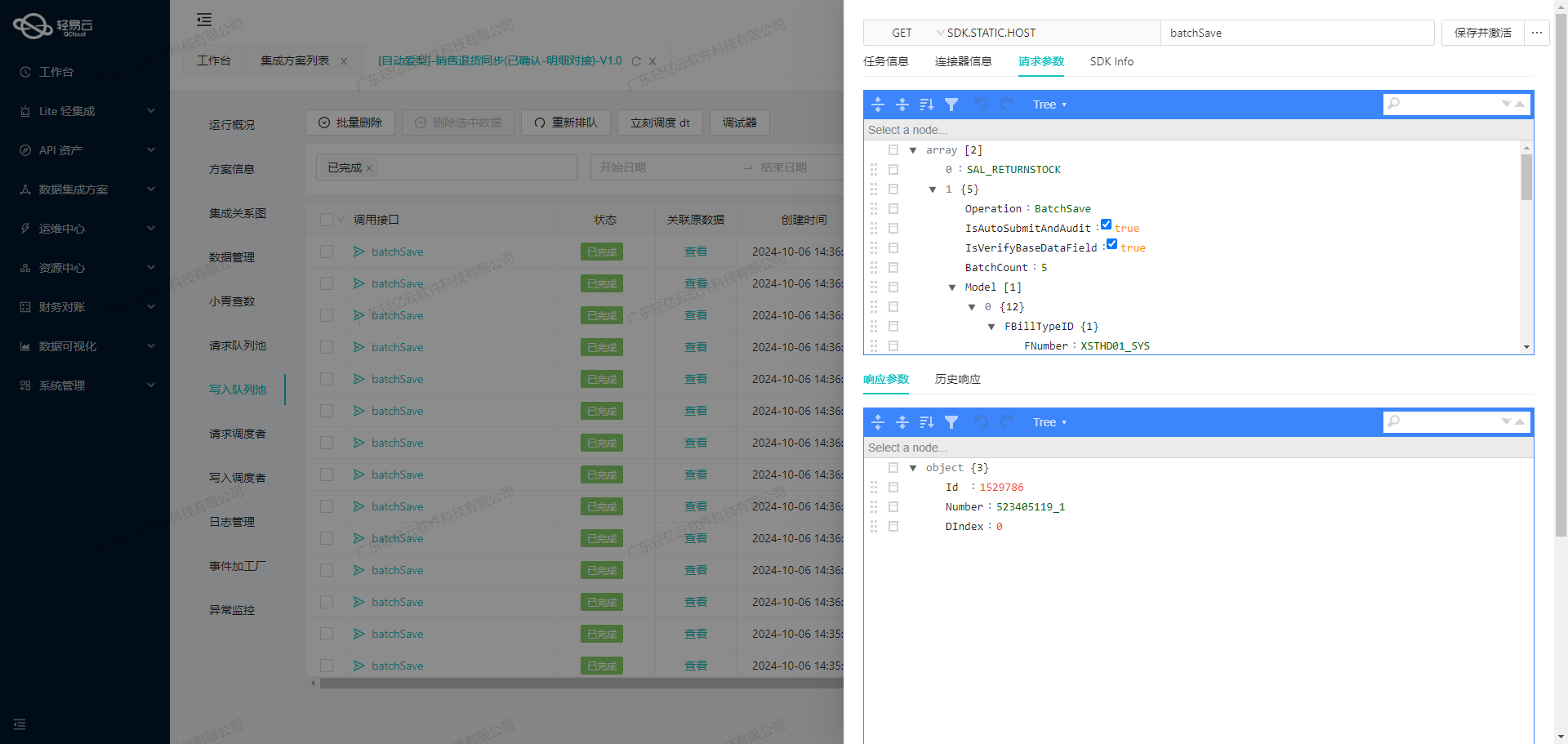
企业信息化管理中的数据集成方案:销售出库单对接
企业信息化管理中的数据集成方案:销售出库单对接 销售出库单旺店通→金蝶:高效数据集成案例分享 在企业信息化管理中,数据的高效流动和准确对接是实现业务流程自动化的关键。本文将聚焦于一个具体的系统对接集成案例:如何将旺店通…...

3.cpp基本数据类型
cpp基本数据类型 1.cpp基本数据类型 1.cpp基本数据类型 C基本数据类型和C语言的基本数据类型差不多 注意bool类型:存储真值 true 或假值 false,C语言编译器C99以上支持。 C语言的bool类型:要添加 #include <stdbool.h>头文件 #includ…...

MCK主机加固与防漏扫的深度解析
在当今这个信息化飞速发展的时代,网络安全成为了企业不可忽视的重要议题。漏洞扫描,简称漏扫,是一种旨在发现计算机系统、网络或应用程序中潜在安全漏洞的技术手段。通过自动化工具,漏扫能够识别出系统中存在的已知漏洞࿰…...

《软件估算之原始功能点:精准度量软件规模的关键》
《软件估算之原始功能点:精准度量软件规模的关键》 一、软件估算的重要性与方法概述二、原始功能点的构成要素(一)数据功能(二)事务功能 三、原始功能点的估算方法(一)功能点分类估算࿰…...

序列化与反序列化
序列化和反序列化是数据处理中的两个重要概念,它们在多种场景下都非常有用,尤其是在分布式系统、网络通信、持久化存储等方面。下面是对这两个概念的详细解释: 序列化(Serialization) 定义:序列化是将对象…...

安装nginx实现多ip访问多网站
[rootlocalhost ~]# systemctl stop firewalld 关防火墙 [rootlocalhost ~]# setenforce 0 关selinux [rootlocalhost ~]# mount /dev/sr0 /mnt 挂载点 [rootlocalhost ~]# dnf install nginx -y 安装nginx [rootlocalhost ~]# nmtui 当前主机添加多地址 [rootlocal…...

每日回顾:简单用C写 冒泡排序、快速排序
冒泡排序 冒泡排序(Bubble Sort)是一种简单的排序算法,它通过重复遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复进行直到没有再需要交换,也就是说该数列已…...

前端_007_Axios库
文章目录 配置响应结构拦截器 引入: 官网: https://www.axios-http.cn/ 一句话简介:浏览器里基于XmlHttpRequests,node.js里基于http模块封装的网络请求库,使用非常方便 //通用例子axios({method:post,url: request…...

NAND FLASH 与 SPI FLASH
面试的时候再有HR针对从数据手册开始做,直接说明:例如RK3588等高速板设计板都有设计指导书,基本把对应的DDR等型号和布局规范都说明,或者DCDC电路直接给一个典型设计原理图,或者BMS更加经典,原理图给的是最…...

QTCreator打不开双击没反应
问题描述 双击后进程里显示有,当过几秒直接消失 解决 找到C\用户\AppData\Roaming\QtProject,删除目录下QtCreator.ini文件(这会重置QtCreator的默认设置),再打开QtCreator时会自动生成对应于默认设置的QtCreator.ini文件&…...

vue npm run ...时 报错-系统找不到指定的路径
vue项目修改时,不知道那一步操作错误了,运行npm run …时报错 系统找不到指定的路径,对此进行记录一下! 解决方法: 1、执行 npm install 命令,重新下载模块 2、根据下方提示执行 npm fund 查看详细信息 …...
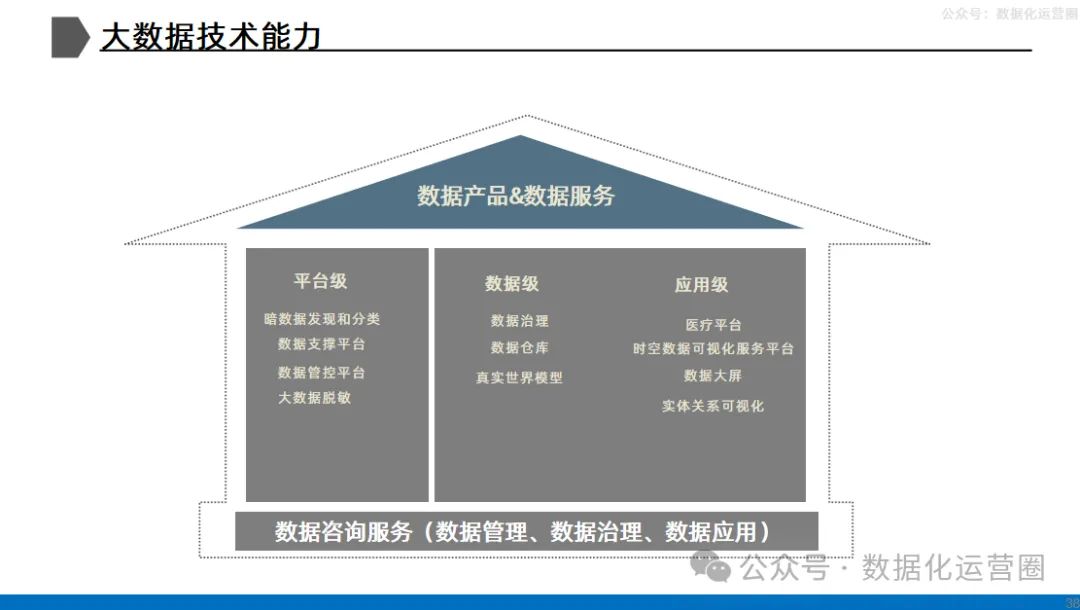
54页可编辑PPT | 大型集团企业数据治理解决方案
这份PPT是关于大型集团企业数据治理的全面解决方案,它详细介绍了数据治理的背景、需求、管理范围、框架、解决思路,以及数据治理在实际操作中的关键步骤。内容涵盖了数据架构、数据质量、数据应用等方面的问题,并提出了数据资产透视、智能搜索…...

STM32嵌入式移植GmSSL库
前言 最近在做一个换电柜的项目,需要和云端平台对接json协议,由于服务端规定了,需要采用sm2 sm3 sm4用来加密。在嵌入式方面只能用北京大学的GmSSL了。 下载GmSSL 在https://github.com/guanzhi/GmSSL下载库 也可以通过git命令下载&#x…...

【mod分享】极品飞车10高清模组,,全新道路,全新建筑,高清植被,全新的道路围栏,全新的天空,画质直逼极品飞车20。支持光追
各位好,今天小编给大家带来一款新的高清重置魔改MOD,本次高清重置的游戏叫《极品飞车10卡本峡谷》。 《极品飞车10:卡本峡谷》该游戏可选择四个模式:生涯、快速比赛、挑战赛、多人连线游戏模式(已不可用)&…...

使用U-KAN训练自己的数据集 — 医疗影像分割
<U-KAN Makes Strong Backbone for Medical Image Segmentation and Generation> U-Net已成为各种视觉应用的基石,如图像分割和扩散概率模型。虽然通过整合变压器或mlp引入了许多创新设计和改进,但网络仍然局限于线性建模模式以及缺乏可解释性。为了应对这些挑战,受到…...

游戏盾在防御DDoS与CC攻击中的作用与实现
随着网络游戏的普及和发展,DDoS(分布式拒绝服务)攻击和CC(Challenge Collapsar)攻击成为了游戏服务器面临的主要威胁之一。游戏盾作为一种专门针对游戏行业设计的防御解决方案,能够在很大程度上减轻甚至消除…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
