PyTorch求导相关
PyTorch是动态图,即计算图的搭建和运算是同时的,随时可以输出结果;而TensorFlow是静态图。
在pytorch的计算图里只有两种元素:数据(tensor)和 运算(operation)
运算包括了:加减乘除、开方、幂指对、三角函数等可求导运算
数据可分为:叶子节点(leaf node)和非叶子节点;叶子节点是用户创建的节点,不依赖其它节点;它们表现出来的区别在于反向传播结束之后,非叶子节点的梯度会被释放掉,只保留叶子节点的梯度,这样就节省了内存。如果想要保留非叶子节点的梯度,可以使用retain_grad()方法。
torch.tensor 具有如下属性:
- 查看 是否可以求导
requires_grad - 查看 运算名称
grad_fn - 查看 是否为叶子节点
is_leaf - 查看 导数值
grad
针对requires_grad属性,自己定义的叶子节点默认为False,而非叶子节点默认为True,神经网络中的权重默认为True。判断哪些节点是True/False的一个原则就是从你需要求导的叶子节点到loss节点之间是一条可求导的通路。
当我们想要对某个Tensor变量求梯度时,需要先指定requires_grad属性为True,指定方式主要有两种:
x = torch.tensor(1.).requires_grad_() # 第一种x = torch.tensor(1., requires_grad=True) # 第二种PyTorch提供两种求梯度的方法:backward() and torch.autograd.grad() ,他们的区别在于前者是给叶子节点填充.grad字段,而后者是直接返回梯度给你,我会在后面举例说明。还需要知道y.backward()其实等同于torch.autograd.backward(y)
一个简单的求导例子是:y=(x+1)∗(x+2) ,计算 ∂y/∂x ,假设给定 x=2
先画出计算图

手算:∂y/∂x=(x+2)*1+(x+1)*1->7
使用backward()
x = torch.tensor(2., requires_grad=True)a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)y.backward()
print(x.grad)
>>>tensor(7.)
看一下这几个tensor的属性
print("requires_grad: ", x.requires_grad, a.requires_grad, b.requires_grad, y.requires_grad)
print("is_leaf: ", x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print("grad: ", x.grad, a.grad, b.grad, y.grad)>>>requires_grad: True True True True
>>>is_leaf: True False False False
>>>grad: tensor(7.) None None None使用backward()函数反向传播计算tensor的梯度时,并不计算所有tensor的梯度,而是只计算满足这几个条件的tensor的梯度:1.类型为叶子节点、2.requires_grad=True、3.依赖该tensor的所有tensor的requires_grad=True。所有满足条件的变量梯度会自动保存到对应的grad属性里。
使用autograd.grad()
x = torch.tensor(2., requires_grad=True)a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)grad = torch.autograd.grad(outputs=y, inputs=x)
print(grad[0])
>>>tensor(7.)因为指定了输出y,输入x,所以返回值就是 ∂x/∂y 这一梯度,完整的返回值其实是一个元组,保留第一个元素就行,后面元素是
二阶求导

求一阶导可以用backward()
x = torch.tensor(2., requires_grad=True)
y = torch.tensor(3., requires_grad=True)z = x * x * yz.backward()
print(x.grad, y.grad)
>>>tensor(12.) tensor(4.)也可以用autograd.grad()
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * ygrad_x = torch.autograd.grad(outputs=z, inputs=x)
print(grad_x[0])
>>>tensor(12.)为什么不在这里面同时也求对y的导数呢?因为无论是backward还是autograd.grad在计算一次梯度后图就被释放了,如果想要保留,需要添加retain_graph=True
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * ygrad_x = torch.autograd.grad(outputs=z, inputs=x, retain_graph=True)
grad_y = torch.autograd.grad(outputs=z, inputs=y)print(grad_x[0], grad_y[0])
>>>tensor(12.) tensor(4.) 再来看如何求高阶导,理论上其实是上面的grad_x再对x求梯度,试一下看
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * ygrad_x = torch.autograd.grad(outputs=z, inputs=x, retain_graph=True)
grad_xx = torch.autograd.grad(outputs=grad_x, inputs=x)print(grad_xx[0])
>>>RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn报错了,虽然retain_graph=True保留了计算图和中间变量梯度, 但没有保存grad_x的运算方式,需要使用creat_graph=True在保留原图的基础上再建立额外的求导计算图,也就是会把 ∂z/∂x=2xy 这样的运算存下来
# autograd.grad() + autograd.grad()
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * ygrad_x = torch.autograd.grad(outputs=z, inputs=x, create_graph=True)
grad_xx = torch.autograd.grad(outputs=grad_x, inputs=x)print(grad_xx[0])
>>>tensor(6.)grad_xx这里也可以直接用backward(),相当于直接从 ∂z/∂x=2xy 开始回传
# autograd.grad() + backward()
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * ygrad = torch.autograd.grad(outputs=z, inputs=x, create_graph=True)
grad[0].backward()print(x.grad)
>>>tensor(6.) 也可以先用backward()然后对x.grad这个一阶导继续求导
# backward() + autograd.grad()
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * yz.backward(create_graph=True)
grad_xx = torch.autograd.grad(outputs=x.grad, inputs=x)print(grad_xx[0])
>>>tensor(6.)那是不是也可以直接用两次backward()呢?第二次直接x.grad从开始回传,我们试一下
# backward() + backward()
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * yz.backward(create_graph=True) # x.grad = 12
x.grad.backward()print(x.grad)
>>>tensor(18., grad_fn=<CopyBackwards>)发现了问题,结果不是6,而是18,发现第一次回传时输出x梯度是12。这是因为PyTorch使用backward()时默认会累加梯度,需要手动把前一次的梯度清零
x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()z = x * x * yz.backward(create_graph=True)
x.grad.data.zero_()
x.grad.backward()print(x.grad)
>>>tensor(6., grad_fn=<CopyBackwards>)向量求导
有没有发现前面都是对标量求导,如果不是标量会怎么样呢?
x = torch.tensor([1., 2.]).requires_grad_()
y = x + 1y.backward()
print(x.grad)
>>>RuntimeError: grad can be implicitly created only for scalar outputs
x = torch.tensor([1., 2.]).requires_grad_()
y = x * xy.sum().backward()
print(x.grad)
>>>tensor([2., 4.])相关文章:

PyTorch求导相关
PyTorch是动态图,即计算图的搭建和运算是同时的,随时可以输出结果;而TensorFlow是静态图。 在pytorch的计算图里只有两种元素:数据(tensor)和 运算(operation) 运算包括了…...

Halcon基础-瓶盖带角度的OCR批量识别
Halcon基础-OCR识别 1、OCR识别素材2、创建路径文件3、Halcon代码实现4、运行效果5、资源获取 1、OCR识别素材 这里我准备了7张不同角度的OCR图片,如下所示: 2、创建路径文件 按照下图所示创建全部文件夹和文件: 01用来存放OCR识别原图 c…...

php语法学习
启动php 进入软件 打开文件:编写代码 $php true; $java false; var_dump($php);//输出变量细节 var_dump($java) 字符串 注意可以使用双引号也可以使用单引号 测试 $php "最好学web语言"; $java 脱胎于c语言; var_dump($php);//输出变量细节 var…...

JavaWeb合集22-Apache POI
二十二、Apache POI Apache POI是一个处理Miscrosoft Office各种文件格式的开源项目。简单来说就是,我们可以使用POI在Java 序中对Miscrosoft Office各种文件进行读写操作。一般情况下,POI都是用于操作Excel文件。 使用场景:银行网银系统导出…...

DDD重构-实体与限界上下文重构
DDD重构-实体与限界上下文重构 概述 DDD 方法需要不同类型的类元素,例如实体或值对象,并且几乎所有这些类元素都可以看作是常规的 Java 类。它们的总体结构是 Name: 类的唯一名称 Properties:属性 Methods: 控制变量的变化和添加行为 一…...

MATLAB Simulink (二)高速跳频通信系统
MATLAB & Simulink (二)高速跳频通信系统 写在前面1 系统原理1.1 扩频通信系统理论基础1.1.1 基本原理1.1.2 扩频通信系统处理增益和干扰容限1.1.3 各种干扰模式下抗干扰性能 1.2 高速跳频通信系统理论基础1.2.1 基本原理1.2.2 物理模型 2 方案设计2…...

智能合约分享
智能合约练习 一、solidity初学者经典示例代码: 1.存储和检索数据: // SPDX-License-Identifier: MIT pragma solidity ^0.8.0; // 声明 Solidity 编译器版本// 定义一个名为 SimpleStorage 的合约 contract SimpleStorage {// 声明一个公共状态变量 d…...
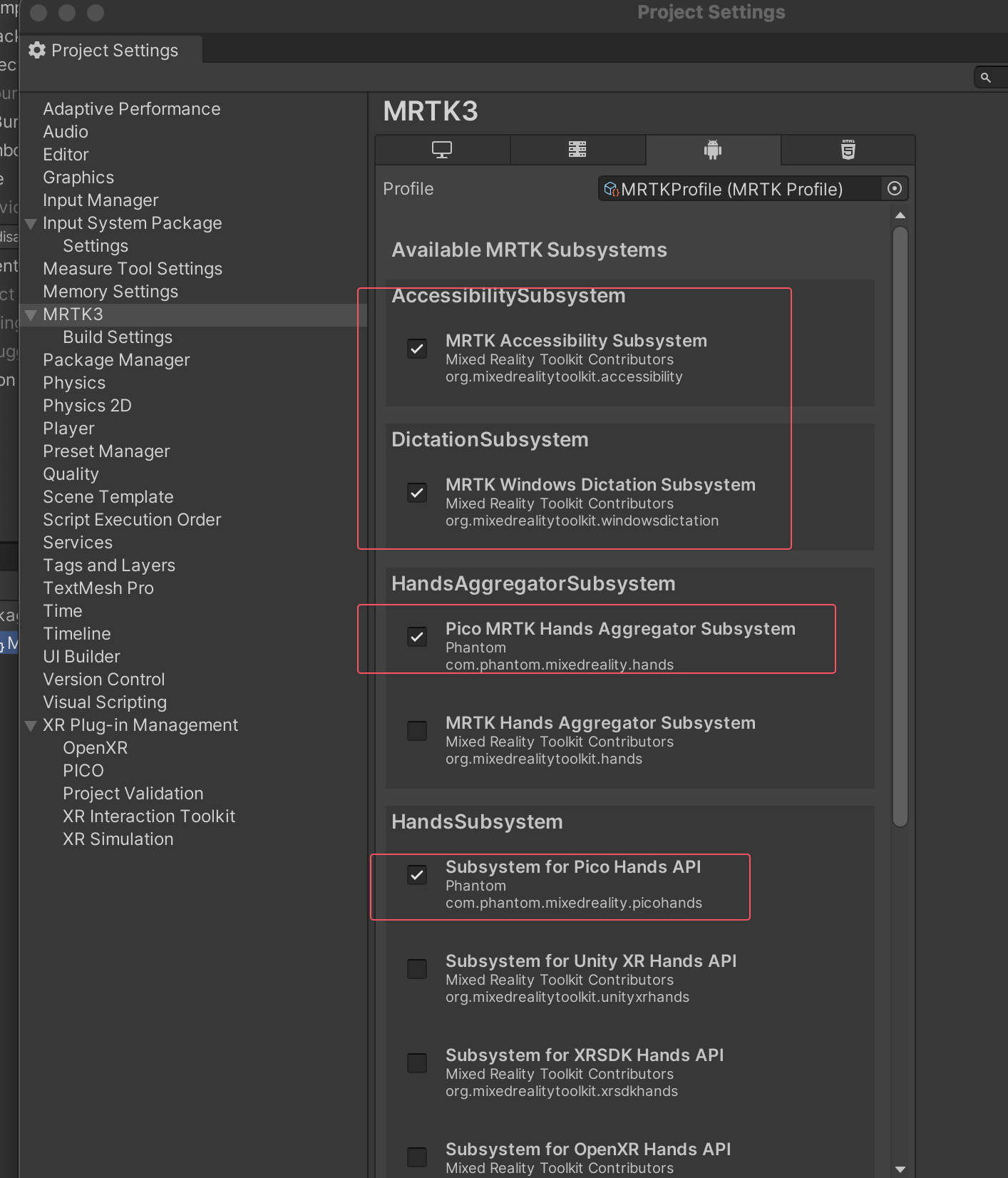
【MR开发】在Pico设备上接入MRTK3(二)——在Unity中配置Pico SDK
上一篇文档介绍了 【MR开发】在Pico设备上接入MRTK3(一)在Unity中导入MRTK3依赖 下面将介绍在Unity中导入Pcio SDK的具体步骤 在Unity中导入Pico SDK 当前Pico SDK版本 Unity交互SDK git仓库: https://github.com/Pico-Developer/PICO-Un…...

【Java】探秘正则表达式:深度解析与精妙运用
目录 引言 一、基本概念 1.1 元字符 1.2 预定义字符类 1.3 边界匹配符 1.4 数量标识符 1.5 捕获与非捕获分组 二、Java中的正则表达式支持 三、正则表达式的使用示例 3.1 匹配字符串 3.2 替换字符串 3.3 分割字符串 3.4 使用Pattern和Matcher 3.5 捕获组和后向…...

2.6.ReactOS系统中从内核中发起系统调用
2.6.ReactOS系统中从内核中发起系统调用 2.6.ReactOS系统中从内核中发起系统调用 文章目录 2.6.ReactOS系统中从内核中发起系统调用前言 前言 上面我们已经可以看到用户空间(R3)进行系统调用的全过程即两种方法的具体实现。 系统调用一般时从R3发起的…...

chat_gpt回答:python获取当前utc时间,将xml里时间tag里的值修改为当前时间
你可以使用 lxml 库来读取、修改 XML 文件中的某个标签的值,并将其保存为新的 XML 文件。以下是一个示例代码,展示如何获取当前的 UTC 时间,并将 XML 文件中的某个时间标签修改为当前时间。 示例代码: from lxml import etree f…...

机器学习-语言分析
机器学习 1.1人工智能概述 1.2.1 机器学习与人工智能,深度学习 深度学习->机器学习->人工智能; 人工智能:1950,实现自动下棋,人机对弈,达特茅斯会议->人工智能的起点,1956年8月。克劳…...

Oracle 常见索引扫描方式概述,哪种索引扫描最快!
一.常见的索引扫描方式 INDEX RANGE SCANINDEX FAST FULL SCANINDEX FULL SCAN(MIN/MAX)INDEX FULL SCAN 二.分别模拟使用这些索引的场景 1.INDEX RANGE SCAN create table t1 as select rownum as id, rownum/2 as id2 from dual connect by level<500000; create inde…...

字符串(3)_二进制求和_高精度加法
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 字符串(3)_二进制求和_高精度加法 收录于专栏【经典算法练习】 本专栏旨在分享学习算法的一点学习笔记,欢迎大家在评论区交流讨论💌 目…...

《神经网络:智能时代的核心技术》
《神经网络:智能时代的核心技术》 一、神经网络的诞生与发展二、神经网络的结构与工作原理(一)神经元模型(二)神经网络训练过程 三、神经网络的应用领域(一)信息领域(二)…...

pdf内容三张以上转图片,使用spire.pdf.free
一、依赖 <spire.pdf.free.version>9.13.0</spire.pdf.free.version><itextpdf.version>5.5.13</itextpdf.version><dependency><groupId>e-iceblue</groupId><artifactId>spire.pdf.free</artifactId><version>$…...

游戏、软件、开源项目和资讯
游戏 标题链接【白嫖正版游戏】IT之家喜加一website 软件 标题链接【白嫖正版软件】反斗限免website 开源项目 标题链接【Luxirty Search】基于Google搜索结果,屏蔽内容农场Github【Video2X】图片/视频超分工具Github 新闻资讯 标题链接分享10个 Claude 3.5 …...

Acrel-1000变电站综合自动化系统及微机在化工企业中的应用方案
文:安科瑞郑桐 摘要:大型化工企业供配电具有的集约型特点,化工企业内35kV变电站和10kV变电所数量大、分布广,对于老的大多大型及中型化工企业而言,其变电站或变电所内高压电气设备为旧式继电保护装置,可靠…...

[Linux] CentOS7替换yum源为阿里云并安装gcc详细过程(附下载链接)
前言 CentOS7替换yum源为阿里云 yum是CentOS中的一种软件管理器,通过yum安装软件,可以自动解决包依赖的问题,免去手工安装依赖包的麻烦。 yum使用了一个中心仓库来记录和管理软件的依赖关系,默认为mirrorlist.centos.org…...

在Java中创建多线程的三种方式
多线程的创建和启动方式 在Java中,创建多线程主要有以下三种方式: 继承Thread类实现Runnable接口使用Callable接口与Future 下面是这三种方式的简单示例,以及如何在主类中启动它们。 1. 继承Thread类 class MyThread extends Thread {Ov…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
