【AI学习】Mamba学习(十二):深入理解S4模型
#1024程序员节|征文#
HiPPO的学习暂告一段落,按照“HiPPO->S4->Mamba 演化历程”,接着学习S4。
S4对应的论文:《Efficiently Modeling Long Sequences with Structured State Spaces》
文章链接:https://ar5iv.labs.arxiv.org/html/2111.00396,https://arxiv.org/abs/2111.00396
上一篇文章初步了解了S4(Structured State Space sequence model)这个序列模型,接下来深入学习一下。
文章的第二章讲述了算法背景,接着学习。从第二章可以看出,发展到S4模型,作者才引入了SSM,而HiPPO那篇论文是没有提到SSM的。
2、S4背景:状态空间

图1中的四个属性描述了状态空间模型(SSM):经典的连续时间表示、用HiPPO框架解决长距离依赖问题、离散时间递归表示,以及可并行化的卷积表示。特别是2.4节介绍了SSM卷积核K,这是我们在第3节中理论贡献的重点。
2.1 状态空间模型:连续时间潜在状态模型
状态空间模型由简单的方程(1)定义。它将一维输入信号u(t)映射到N维潜在状态x(t),然后投影到一维输出信号y(t)。

SSM在许多科学学科中广泛使用,并且与潜在状态模型如隐马尔可夫模型(HMM)相关。我们的目标是简单地将SSM作为一个黑盒表示,用于深度序列模型,其中A、B、C、D是梯度下降学习的参数。在本文的其余部分,为了表述方便,我们将省略参数D(或者等价地,假设D = 0),因为项Du可以被视为一个跳跃连接,并且容易计算。
前面说过,Du项相当于残差连接,而整个模型中一般也有残差连接,可以合并到整个模型,而在SSM方程这里省略。
2.2 用HiPPO解决长距离依赖问题
先前的工作发现基本的SSM(1)在实践中实际上表现非常差。直观地,一个解释是线性一阶ODEs解决为指数函数,因此可能遭受梯度在序列长度上呈指数增长(即,梯度消失/爆炸问题[32])。为了解决这个问题,线性状态空间层(LSSL)利用了连续时间记忆的HiPPO理论[16]。HiPPO指定了一类特定的矩阵A∈RN×N,当它们被纳入(1)时,允许状态x(t)记忆输入u(t)的历史。这个类别中最重要的矩阵由方程(2)定义,我们将称之为HiPPO矩阵。例如,LSSL发现简单地将SSM从随机矩阵A修改为方程(2)将其在顺序MNIST基准测试上的性能从60%提高到98%。

2.3 离散时间SSM:递归表示
为了在离散输入序列(u0, u1, …)上应用而不是连续函数u(t),(1)必须通过一个步长∆来离散化,该步长表示输入的分辨率。从概念上讲,输入uk可以被视为对隐含的连续信号u(t)的采样,其中uk = u(k∆)。
为了离散化连续时间SSM,我们遵循先前的工作,使用双线性方法[43],将状态矩阵A转换为近似A。离散SSM是:

方程(3)现在是序列到序列的映射uk → yk,而不是函数到函数的映射。此外,状态方程现在是一个递归的xk,允许离散SSM像RNN一样计算。具体来说,xk ∈ RN可以被视为具有转换矩阵 的隐藏状态。
的隐藏状态。
从符号上讲,本文中我们使用 、
、 、…来表示由(3)定义的离散SSM矩阵。注意,这些矩阵是A和步长∆的函数;当它清晰时,我们为了符号方便而省略了这种依赖。
、…来表示由(3)定义的离散SSM矩阵。注意,这些矩阵是A和步长∆的函数;当它清晰时,我们为了符号方便而省略了这种依赖。
2.4 训练SSM:卷积表示
递归SSM(3)不适用于在现代硬件上进行训练,因为它是顺序的。相反,线性时不变(LTI)SSM(如(1))和连续卷积之间有一个众所周知的联系。相应地,(3)实际上可以写成一个离散卷积。
为了简单起见,让初始状态为x−1 = 0。然后展开(3)得到

这可以向量化为一个卷积(4),并为卷积核(5)提供一个明确公式。

换句话说,方程(4)是一个单一的(非循环)卷积,并且可以使用FFTs高效计算,前提是K是已知的。然而,计算(5)中的K并非易事,这是我们在第3节中技术贡献的重点。我们称K为SSM卷积核或滤波器。
个人说明
前面介绍部分就提到“SSM由于具体的理论原因,它尚未适用于深度学习。深度 SSM 实际上即使在简单的任务上也很困难,但当配备最近为解决连续时间记忆(就是HiPPO)问题而导出的特殊状态矩阵 A 时,可以表现得非常好”。第二章部分进一步阐释,“基本的 SSM在实践中表现非常差。直观地说,一种解释是线性一阶常微分方程解为指数函数,因此可能会受到序列长度中梯度指数缩放的影响(即消失/爆炸梯度问题)。”其实,熟悉RNN的训练就会知道,RNN的训练就面临梯度爆炸或消失的问题。
S4 这里选取的矩阵 A 为 HiPPO-LegS的矩阵形式, 但是LegS 所满足的 ODE 是矩阵A、B下面要除以t的。就是下面的形式:

不知道为啥HiPPO-LegS的矩阵形式直接用到SSM方程效果就可以很好。
这里面有点奇怪,回头需要再看看相关论文:《Legendre memory units: Continuous-time representation in recurrent neural networks. In Advances in Neural Information Processing Systems, pages 15544–15553, 2019.》
苏神在文章《重温状态空间模型SSM:HiPPO的高效计算(S4)》也进行了分析,这种修改之后,导致时间度量无法对整个历史平均的取权重,而是历史信息呈现指数衰减的效应,就是更看重时间较近的信息。
离散时间 SSM这里的离散化还是使用了双线性的近似方式,没有采用解析解。要在后面Mamba模型才使用离散化的解析解。
在前面介绍部分,就提到,深层 SSM 原则上可以解决 LRD 问题,但是由于状态表示引起的计算和内存要求过高,LSSL 在实践中不可行。以及,“尽管提出了 LSSL 的 理论上有效的算法,但这些算法在数值上是不稳定的。特别是,特殊 A 矩阵在线性代数意义上是高度非正规的,这阻碍了传统算法技术的应用。因此,尽管 LSSL 表明 SSM 具有很强的性能,但它们目前作为通用序列建模解决方案在计算上是不切实际的。”这就引出了下一章,具体的S4方法。
注:正规矩阵的一个重要性质是它可以经过一个酉变换变为对角矩阵。厄米矩阵(Hermitian matrices)和酉矩阵(unitary matrices)都是正规矩阵的典型例子。
3、Method: Structured State Spaces (S4)
具体方法,咱们直接跳到最终方法部分:

这个方法,就是把HiPPO 矩阵A分解为正规矩阵和低秩矩阵的和。这个分解的目的,就是为了方便的实现矩阵A的对角化。
为什么要对角化?为了计算简便。前面的公式5的卷积形式,矩阵A的L次幂,如果是对角矩阵,计算就可以大大简化。
文章3.1节,给出了这种对角化动机的目的。

但是文章接着说,不幸的是,由于数值问题,对角化的简单应用在实践中不可行。尽管有其他方法,数值上也不稳定。
那怎么办,3.2节给出方法:将HiPPO 矩阵A分解为正态矩阵和低秩矩阵的和。这样处理后获得了一个反对称矩阵,“重点来了,反对称矩阵不单单一定可以对角化,它一定可以被正交矩阵(复数域叫做酉矩阵)对角化!酉矩阵一般数值稳定性都非常好”。

这里的生成函数如何理解?其实也简单,熟悉卷积运算的就知道,卷积运算计算量大,可以先做FFT,在频域变成乘法,然后IFFT。这是利用FFT的简化卷积运算经常使用的方法。只不过,这里傅立叶变换所需要的实际是“截断生成函数”,将无限长度截断为L。

最后,再总结一下S4的架构细节。

具体第三章涉及的公式推导,可以参见苏神在文章《重温状态空间模型SSM:HiPPO的高效计算(S4)》中的详细推导。
最后
再重温一下上篇《Mamba学习(十一):S4》提到的问题和S4的方法:
解决的主要问题
- 序列建模中长距离依赖(LRDs)的有效处理。
- 现有模型在处理非常长序列时的局限性。
- 先前基于SSM的方法在计算和内存需求上的高成本问题。
方法
- 提出了S4模型,它基于SSM的新参数化,通过将状态矩阵A分解为低秩和正规项的和,使得A可以被稳定地对角化。
- 利用Woodbury identity和Cauchy核的计算,将SSM的计算复杂度从O(N^2L)降低到O(N+L),其中N是状态维度,L是序列长度。
- 在多个任务和数据集上验证了S4模型的性能,包括顺序CIFAR-10、WikiText-103语言建模、图像分类和时间序列预测等。
相关文章:

【AI学习】Mamba学习(十二):深入理解S4模型
#1024程序员节|征文# HiPPO的学习暂告一段落,按照“HiPPO->S4->Mamba 演化历程”,接着学习S4。 S4对应的论文:《Efficiently Modeling Long Sequences with Structured State Spaces》 文章链接:https://ar5iv…...

linux入门之必掌握知识点
#1024程序员节|征文# Linux基础 top命令详解 top命令是用来查看进程系统资源使用情况的工具,它可以动态的现实。 top命令执行后,按大写M可以按内存使用情况进行排序,大写P可以按CPU使用情况进行排序,大写H可以显示线…...

【Web.路由]——路由原理
这篇文章,我们来讲一讲什么是路由。 路由是 将用户请求地址映射为一个请求委托的过程,负责匹配传入的Http请求,然后将这些请求发送到应用的可执行终结点。 这里需要注意一个内容,发送到应用的可执行终结点。 路由的分类&#x…...

Spring Boot技术在中小企业设备管理中的应用
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...
)
Lua表(Table)
软考鸭微信小程序 过软考,来软考鸭! 提供软考免费软考讲解视频、题库、软考试题、软考模考、软考查分、软考咨询等服务 Lua中的表(table)是一种核心数据结构,它既是数组也是字典,能够存储多种类型的数据,包括数字、字符…...

51单片机应用开发(进阶)---外部中断(按键+数码管显示0-F)
实现目标 1、巩固数码管、外部中断知识 2、具体实现:按键K4(INT1)每按一次,数码管从0依次递增显示至F,再按则循环显示。 一、共阳数码管 1.1 共阳数码管结构 1.2 共阳数码管码表 共阳不带小数点0-F段码为ÿ…...

怎么区分主谓宾I love you与主系表I am fine? 去掉宾语看句子完整性 主系表结构则侧重于描述主语的状态、特征或性质
主谓宾与主系表是英语句子结构中的两种基本类型,它们在关注点、动词分类以及句子完整性方面有所区别。具体分析如下: 关注点 主谓宾I love you:主谓宾结构主要关注动作和影响对象之间的关系[1]。这种结构强调的是动态和行为,通常描…...

私域流量运营的误区
私域流量运营是近年来营销领域的重要趋势,但在实际操作中,很多企业和个人容易陷入一些误区。以下是几个常见的私域流量运营误区及其解决方法: 1. 只关注流量,不重视内容 误区:许多运营者认为,只要吸引到足…...

VirtualBox虚拟机桥接模式固定ip详解
VirtualBox虚拟机桥接模式固定ip详解 VirtualBox 桥接设置Ubuntu 24.04使用固定IP问题记录 VirtualBox 桥接设置 为什么设置桥接模式?桥接模式可以实现物理机和虚拟机互相通信,虚拟机也可以访问互联网(推荐万金油),物…...

面试问题基础记录24/10/24
面试问题基础记录24/10/24 问题一:LoRA是用在节省资源的场景下,那么LoRA具体是节省了内存带宽还是显存呢?问题二:假如用pytorch完成一个分类任务,那么具体的流程是怎么样的?问题三:详细介绍一下…...

中国区 Microsoft365主页链接请您参考:
Microsoft365主页链接请您参考: Redirecting PPAC链接请您参考: Power Platform admin center 关于Power Automate开启工单是在 https://portal.partner.microsoftonline.cn/Support/SupportOverview.aspx进行提交的。 对应所需对应管理员可以分配以下…...

Go encoding/json库
JSON在网络上广泛使用,是一种基于文本的数据传输方式。在本集中,我们将与 Daniel Marti 一起探索 Go 的 encoding/json 包和其他包。 本篇内容是根据2020年7月份[#141 {“encoding”:“json”}](https://changelog.com/gotime/141 “#141 {“encoding”…...
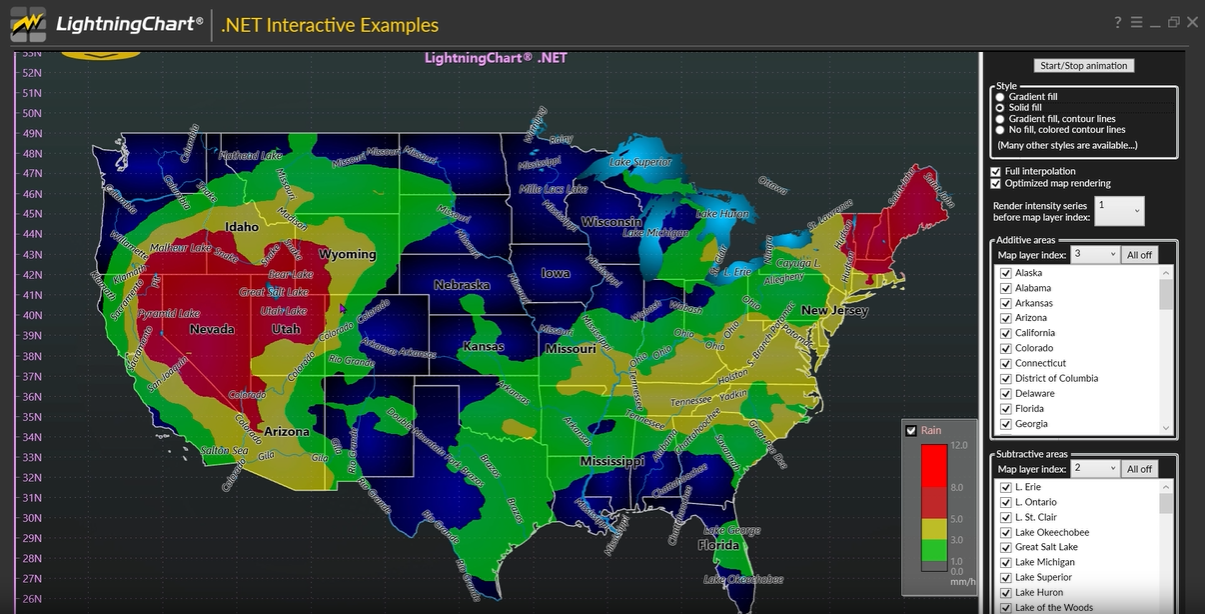
「实战应用」如何用图表控件LightningChart可视化天气数据?(二)
LightningChart.NET完全由GPU加速,并且性能经过优化,可用于实时显示海量数据-超过10亿个数据点。 LightningChart包括广泛的2D,高级3D,Polar,Smith,3D饼/甜甜圈,地理地图和GIS图表以及适用于科学…...

苹果瑕疵数据集苹果质量数据集YOLO格式VOC格式 深度学习 目标检测 数据集
一、数据集概述 数据集名称:2类苹果图像数据集 数据集包含两类样本:正常苹果和有瑕疵的苹果。正常苹果样本代表完好的苹果,而有瑕疵的苹果样本代表苹果表面可能存在的损伤、瑕疵或病害。每个样本都经过详细标记和描述,以便训练模…...
旧电脑安装Win11提示“这台电脑当前不满足windows11系统要求”,安装中断。怎么办?
前言 最近有很多小伙伴也获取了LTSC版本的Win11镜像,很大一部分小伙伴安装这个系统也是比较顺利的。 有顺利安装完成的,肯定也有安装不顺利的。这都是很正常的事情,毕竟这个镜像对电脑硬件要求还是挺高的。 有一部分小伙伴在安装Windows11 …...

深入理解QT多线程编程
文章目录 多线程用法QThread类QtConcurrent类QFutureSynchronizer类获取线程信息线程优先级获取线程状态线程局部存储使用线程池监听线程事件Qt是一个跨平台的应用程序开发框架,广泛应用于图形用户界面(GUI)开发。它提供了强大的多线程支持,允许开发者在应用程序中创建和管理…...

React四官方文档总结一UI与交互
代码下载 React官网已经都是函数式组件文档,没有类组件文档,但是还是支持类组件这种写法。 UI 描述 组件 组件 是 React 的核心概念之一,它们是构建用户界面(UI)的基础。React 允许你将标签、CSS 和 JavaScript 组…...

如何理解 HTTP 是无状态的,以及它与 Cookie 和 Session 之间的联系
文章目录 一、什么是 HTTP?无状态的含义 二、为什么 HTTP 是无状态的?三、Cookie 和 Session 的引入1. Cookie特点:示例: 2. Session特点:示例(Java Servlet): 四、HTTP、Cookie 和 …...

OpenCV视觉分析之运动分析(2)背景减除类:BackgroundSubtractorKNN的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 K-最近邻(K-nearest neighbours, KNN)基于的背景/前景分割算法。 该类实现了如 319中所述的 K-最近邻背景减除。如果前景…...

android黑屏问题记录
近期出现了一个黑屏问题: 仪表显示,主副屏黑的 :原因背光开启太晚,导致拍照时候是黑的,太晚的原因是绘制进程出现异常导致重启延后了时间,绘制进程crash原因是hwc调用底层库卡住,需更新hwc对应的…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
