分布式解决方案---分布式ID
目录
是什么
特点
全局唯一
高并发
高可用
怎么做
实现方案
是什么
分布式ID是指在分布式系统中生成的唯一标识符。由于分布式系统的特点,多个节点可能会同时生成ID,因此需要确保每个ID在整个系统中是唯一的。
重点就是唯一性!!!!
特点
-
全局唯一
-
高并发
-
高可用
怎么做
-
UUID
-
缺点:长 占用空间大 无序的放到数据库做id索引性能下降
-
java实现
public static void main(String[] args) {// 生成随机UUIDUUID uuid = UUID.randomUUID();// 将UUID转换为字符串String uuidString = uuid.toString();// 输出UUIDSystem.out.println("生成的UUID: " + uuidString);}
-
-
数据库主键自增
-
缺点:并发性能不高,分库分表比较麻烦,自增泄露数据库数据量
-
-
Redis自增
-
缺点:自增泄露数据量, 不够稳定,会造成数据丢失,redis负载过高的情况下造成ID生成速度慢
-
-
雪花算法
-
缺点:时钟回拨(可以解决,选用)
-
实现方案
推荐 美团Leaf
相关文章:

分布式解决方案---分布式ID
目录 是什么 特点 全局唯一 高并发 高可用 怎么做 实现方案 是什么 分布式ID是指在分布式系统中生成的唯一标识符。由于分布式系统的特点,多个节点可能会同时生成ID,因此需要确保每个ID在整个系统中是唯一的。 重点就是唯一性!&#x…...

httpd服务
文章目录 1、搭建一个网络yum源2、基于域名访问的虚拟主机3、基于端口来访问域名4、搭建个人网站5、加密访问显示自定义网页内容 1、搭建一个网络yum源 [roottest01 conf.d]# cat repo.conf <virtualhost *:80>documentroot /var/www/html/ServerName 10.104.43.154ali…...
Linux系统安装Redis详细操作步骤(二进制发布包安装方式)
安装方式介绍 在Linux系统中,安装软件的方式主要有四种,这四种安装方式的特点如下: 安装方式特点二进制发布包安装软件已经针对具体平台编译打包发布,只要解压,修改配置即可rpm安装软件已经按照redhat的包管理规范进…...
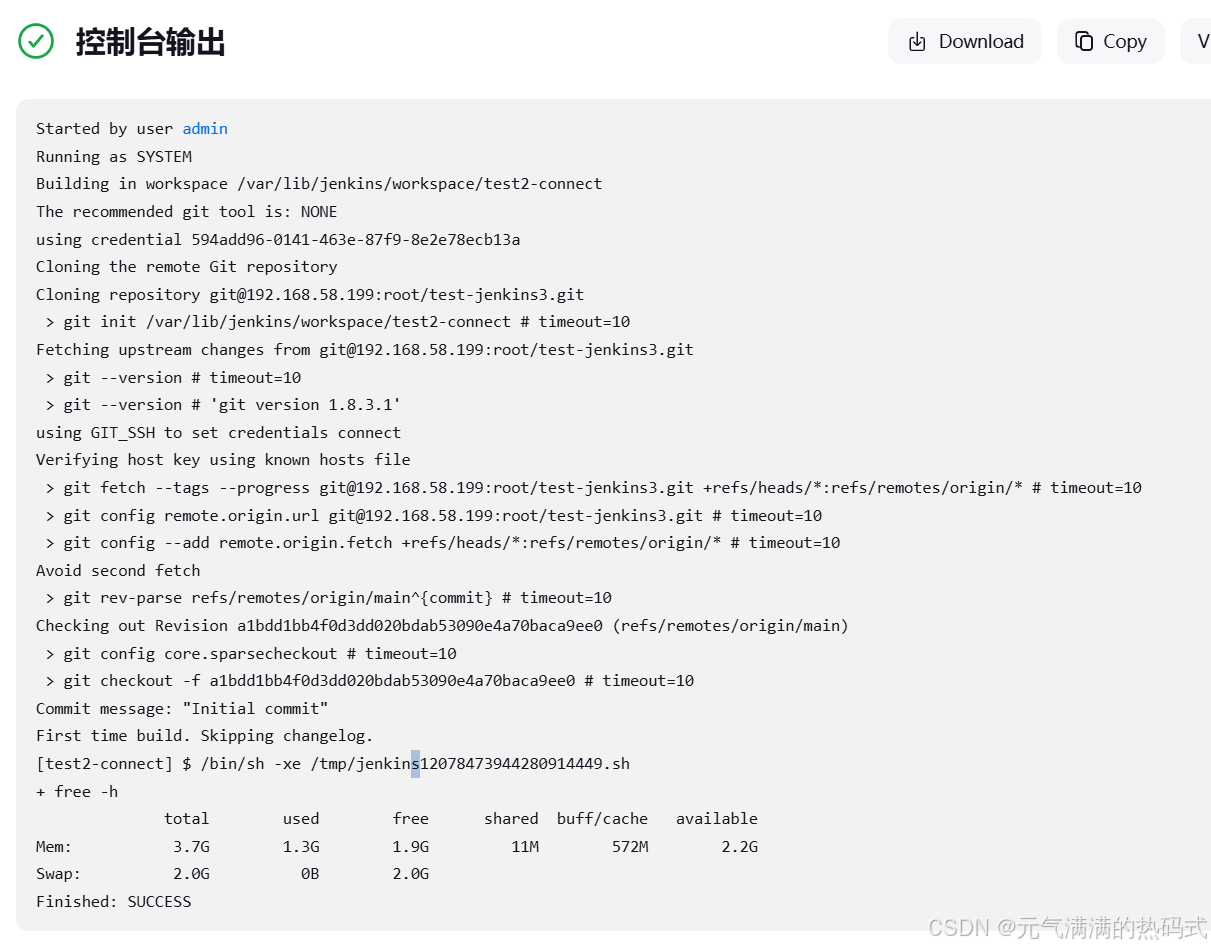
Jenkins和Gitlab整合构建CI/CD流水线
配置环境 虚拟机建议4G起步 192.168.58.199 192.168.58.200 部署Jenkins 部署Jenkins参考这篇文章:Jenkins安装部署_connecting to pkg.jenkins.io (pkg.jenkins.io)|151.-CSDN博客 安装完毕之后根据下图操作 选择git,添加git仓库克隆url,选…...

14 C语言中的关键字
C语言中的关键字 在C语言中,关键字是一些预定义的单词,它们具有特殊的意义和用途。这些关键字不能用作标识符,比如变量名、函数名等,因为它们被保留用于特定的语言结构和操作。 关键字的分类 C语言的关键字可以分为几个主要类别…...

(11)(2.1.7) FETtec OneWire ESCs(一)
文章目录 前言 1 去哪里买 2 连接 3 组态 前言 !Note 此功能在固件版本 4.1.1 及更高版本上可用。 OneWire 是 FETtec 的 ESC 双向通信协议(ESC bi-directional communication protocol)。 FETtec OneWire ESC 的遥测信息被发送回自动驾驶仪: 电…...

Python 异步编程:使用 `asyncio.to_thread` 和 `asyncio.Queue` 处理任务队列
Python 异步编程:使用 asyncio.to_thread 和 asyncio.Queue 处理任务队列 1. 什么是 asyncio.to_thread?2. 什么是 asyncio.Queue?3. 示例代码:使用 asyncio.to_thread 和 asyncio.Queue 处理任务队列示例代码代码解释运行结果 4.…...
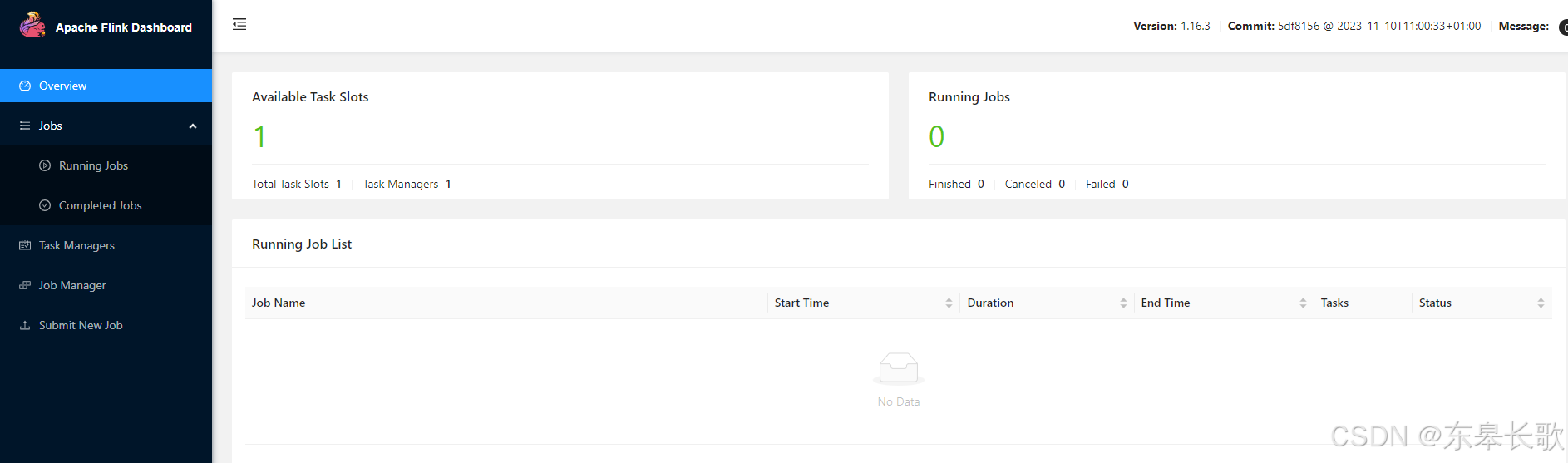
【问题解决】Flink在linux上运行成功但是无法访问webUI界面
一,问题 在搭建Flink的时候,已经在linux服务器上运行了./start-cluster.sh, 而且日志显示已经成功了。 服务器上也没有开启防火墙 正常来说应该能通过ip:8081来访问(8081是Flink WebUI的默认端口),但是访问的时候,显示…...

【问题解决】pnpm : 无法将“pnpm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。
今天配置完poetry环境变量之后pnpm不能用了 具体报错 pnpm : 无法将“pnpm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确保路径正确,然后再试一次。 所在位置 行:1 字符: 1pnpm run dev~~~~ Ca…...
微信网页授权回调地址放多个参数的方法
https://open.weixin.qq.com/connect/oauth2/authorize?appidAPPID&redirect_uriREDIRECT_URI&response_typecode&scopeSCOPE&stateSTATE#wechat_redirect 跳转后地址 redirect_uri/?codeCODE&stateSTATE。 redirect_uri如果不进行urlencode编码, 跳转后…...

相机工作距离计算
镜头 基础参数 焦距 例如,使用1英寸靶面(12.8mm x 9.6mm)的相机,工作距离WD是300mm,视野FOV的高度是120mm,那么光学放大倍率𝛽 9.6𝑚𝑚/120𝑚𝑚0.08 ,…...

Pandas模块之垂直或水平交错条形图
目录 df.plot() 函数Pandas模块之垂直条形图Pandas模块之水平交错条形图 df.plot() 函数 df.plot() 是 Pandas 中的一个函数,用于绘制数据框中的数据。它是基于 Matplotlib 库构建的,可以轻松地创建各种类型的图表,包括折线图、柱状图、散点…...
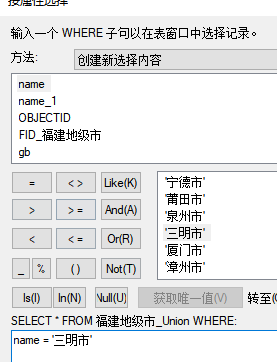
ArcGIS必会的选择要素方法(AND、OR、R、IN等)位置选择等
今天来看看ArcGIS中的几个选择的重要使用方法 1、常规选择、 2、模糊查询、 3、组合复合条件查询(AND、OR、IN), 4、空值NULL查询 5、位置选择 推荐学习: 以梦为马,超过万名学员学习ArcGIS入门到实战的应用课程…...

快速创建一个微信小程序,详细步骤以及示范程序代码
创建一个微信小程序涉及前端和后端的搭建与联调。以下是一个快速创建微信小程序的详细步骤以及示范程序代码。 一、注册微信小程序账号 前往微信公众平台,注册一个小程序账号并完成相关设置。注册完成后,获取小程序的AppID,这是后续开发过程…...

【继承】讲解
访问控制 传递下去可以一共分为四个特性 公有保护私有存在但不可见 虽然它们各自的特性不同,能不能使用也另说,但是在建立类对象的时候,系统都会申请相应的内存,也就是说,无论它们能不能用,它们都存在。 …...

无人机之低空管控技术
无人机的低空管控技术是对低空飞行活动进行管理和控制的一系列措施和技术的总称,旨在确保低空飞行活动的安全、有序和高效。 一、主要技术手段 雷达系统监测 原理:雷达是利用电磁波探测目标的电子设备,通过发射电磁波对目标进行照射并接收…...

探索 DevOps:从概念到实践
引言 在现代软件开发的世界中,DevOps 已成为一个热门词汇。它不仅改变了开发和运维的合作方式,还显著提升了软件交付的速度和质量。那么,究竟什么是 DevOps?它的定义和目标是什么?本文将为你详细解释 DevOps 的基本概念,并通过代码示例和图片帮助你更好地理解这一重要的…...

联通国际云视频:高清、稳定、易用的云端会议平台
一、产品概述 中国联通国际公司推出的云视频产品,是一款基于先进云计算技术的云会议架构平台。它旨在为用户提供高品质、方便快捷、简单易用、灵活多变、稳定可靠的视频通讯解决方案,满足用户随时随地高效沟通的需求。 二、主要功能 音视频及数据共享 …...
)
表达式求值(2020cspj)
题目描述 给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。 输入格式 一行,为需要你计算的表达式,表达式中只包含数字、加法运算符 和乘法运算符 *,且没有括号,所有参与运算的数字均为 0 到 231−1…...

算法的学习笔记—数组中只出现一次的数字(牛客JZ56)
😀前言 在数组中寻找只出现一次的两个数字是一道经典的问题,通常可以通过位运算来有效解决。本文将详细介绍这一问题的解法,深入解析其背后的思路。 🏠个人主页:尘觉主页 文章目录 🥰数组中只出现一次的数字…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
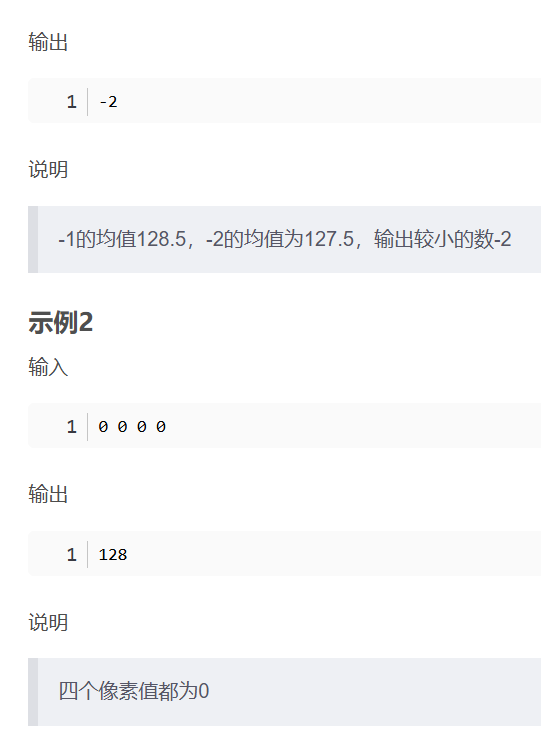
华为OD机考- 简单的自动曝光/平均像素
import java.util.Arrays; import java.util.Scanner;public class DemoTest4 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint[] arr Array…...

Android Settings 数据库生成、监听与默认值配置
一、Settings 数据库生成机制 传统数据库生成(Android 6.0 前) 路径:/data/data/com.android.providers.settings/databases/settings.db创建流程: SQL 脚本初始化:通过 sqlite 工具创建数据库文件…...

AcWing 3417:砝码称重——位集合
【题目来源】 3417. 砝码称重 - AcWing题库 【题目描述】 你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1,W2,⋅⋅⋅,WN。 请你计算一共可以称出多少种不同的正整数重量? 注意砝码可以放在天平两边。 【输入格式】 输入的第一行包含一个整数 N。 …...
