Go语言基础教程:可变参数函数
Go 语言允许函数接收可变数量的参数,这种特性对于处理数量不确定的参数特别有用。在本教程中,我们将通过示例代码讲解如何定义和使用 Go 的可变参数函数。
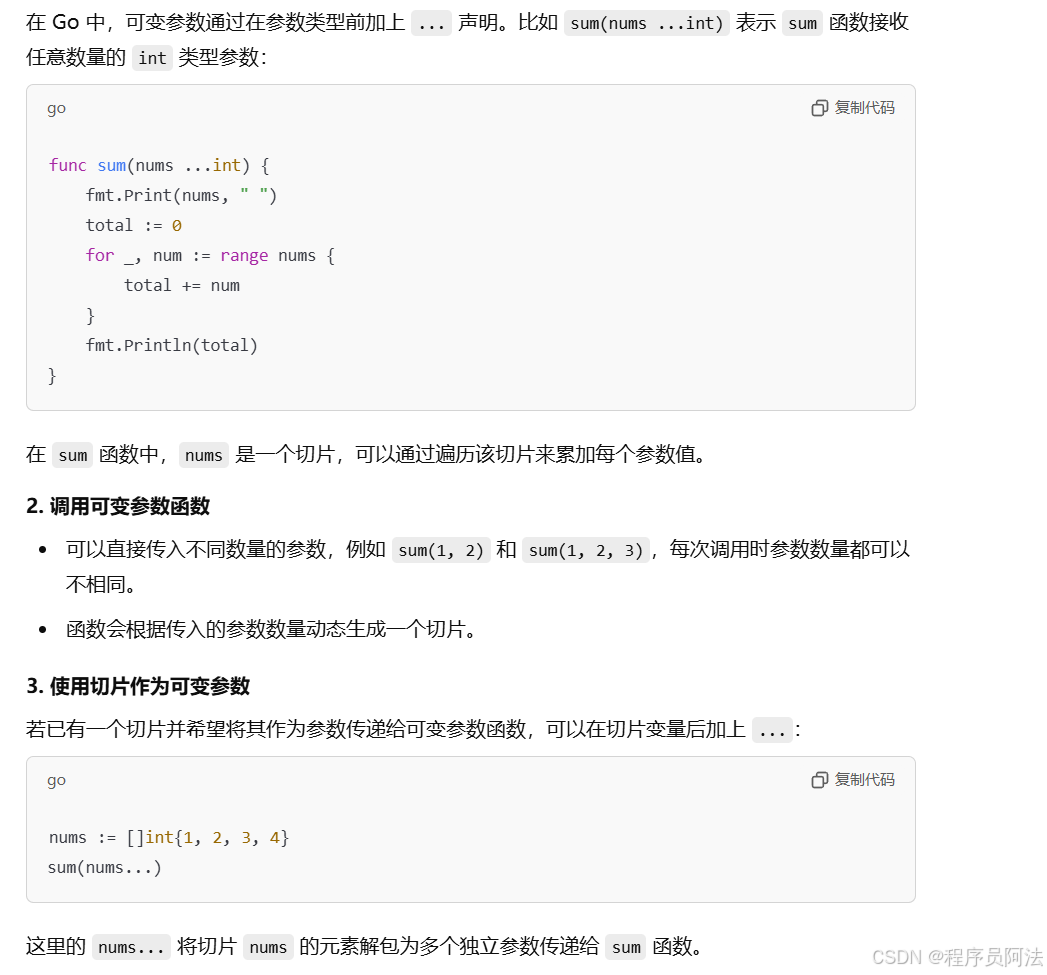
package mainimport "fmt"// 定义一个可变参数函数 sum,接收任意数量的整型参数
func sum(nums ...int) {fmt.Print(nums, " ")total := 0for _, num := range nums {total += num}fmt.Println(total)
}func main() {// 直接传入不同数量的参数sum(1, 2) // 输出: [1 2] 3sum(1, 2, 3) // 输出: [1 2 3] 6// 使用切片作为参数nums := []int{1, 2, 3, 4}sum(nums...) // 输出: [1 2 3 4] 10
}
相关文章:

Go语言基础教程:可变参数函数
Go 语言允许函数接收可变数量的参数,这种特性对于处理数量不确定的参数特别有用。在本教程中,我们将通过示例代码讲解如何定义和使用 Go 的可变参数函数。 package mainimport "fmt"// 定义一个可变参数函数 sum,接收任意数量的整…...

高并发场景下解决并发数据不一致
简单的场景: 全量数据更新的情况下, 不在乎同一秒的请求都必须要成功, 只留下最新的更新请求数据 方案常用的是 1、数据库增加时间戳标识实现的乐观锁, 请求参数从源头带上微秒或者毫秒时间戳数据库存储, 然后在更新SQL语句上比较 (数据库的时间 < 参数传递的时间) 例如: A…...
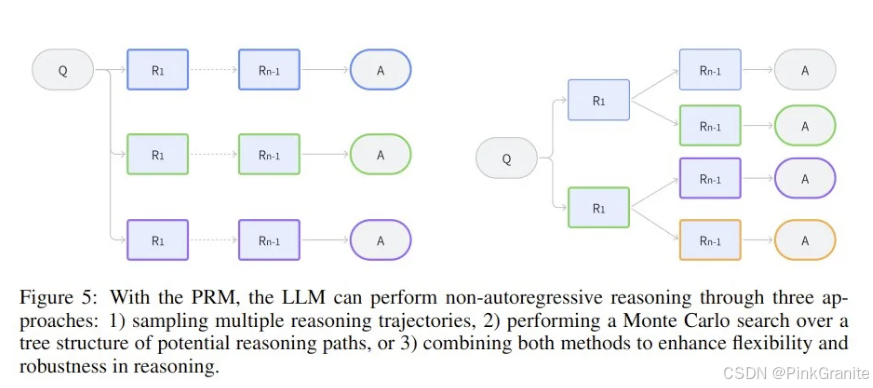
OpenAI GPT-o1实现方案记录与梳理
本篇文章用于记录从各处收集到的o1复现方案的推测以及介绍 目录 Journey Learning - 上海交通大学NYUMBZUAIGAIRCore IdeaKey QuestionsKey TechnologiesTrainingInference A Tutorial on LLM Reasoning: Relevant methods behind ChatGPT o1 - UCL汪军教授Core Idea先导自回归…...
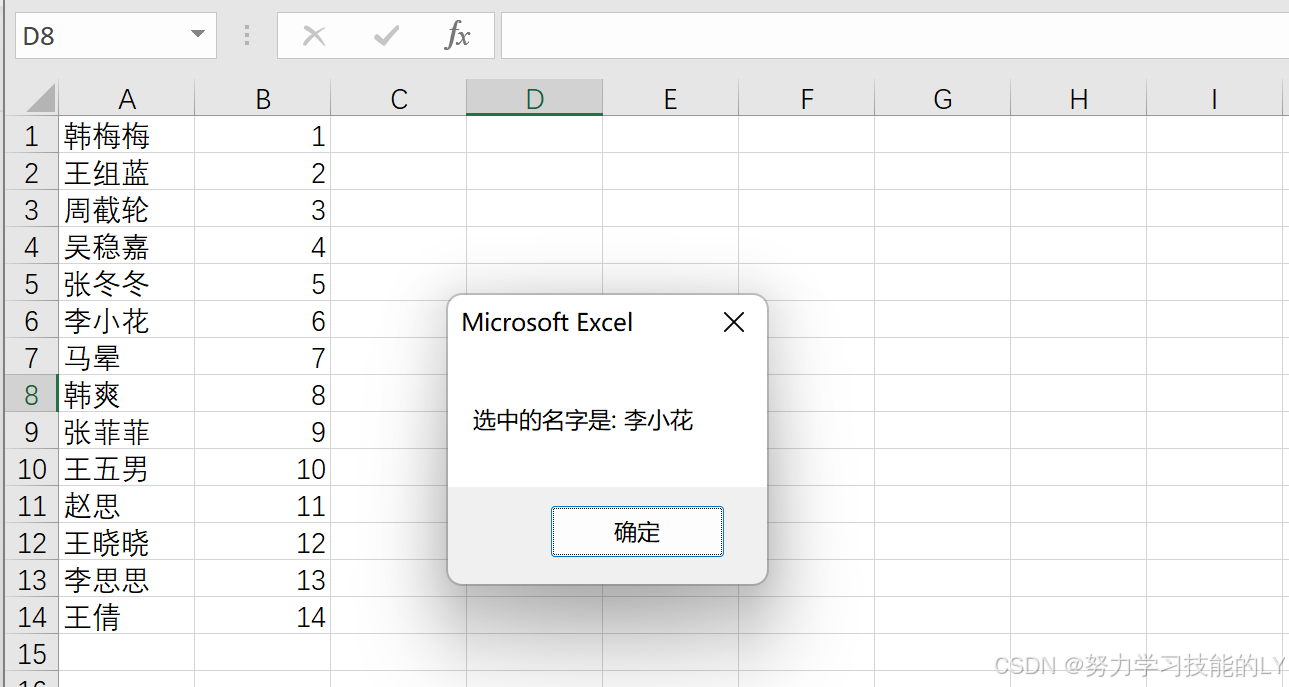
Excel:vba实现生成随机数
Sub 生成随机数字()Dim randomNumber As IntegerDim minValue As IntegerDim maxValue As Integer 设置随机数的范围(假入班级里面有43个学生,学号是从1→43)minValue 1maxValue 43 生成随机数(在1到43之间生成随机数)randomNumber Application.WorksheetFunctio…...

Python | Leetcode Python题解之第506题相对名次
题目: 题解: class Solution:desc ("Gold Medal", "Silver Medal", "Bronze Medal")def findRelativeRanks(self, score: List[int]) -> List[str]:ans [""] * len(score)arr sorted(enumerate(score), …...
)
安全见闻(6)
声明:学习视频来自b站up主 泷羽sec,如涉及侵权马上删除文章 感谢泷羽sec 团队的教学 视频地址:安全见闻(6)_哔哩哔哩_bilibili 学无止境,开拓自己的眼界才能走的更远 本文主要讲解通讯协议涉及的安全问题。…...

Promise、async、await 、异步生成器的错误处理方案
1、Promise.all 的错误处理 Promise.all 方法接受一个 Promise 数组,并返回所有解析 Promise 的结果数组: const promise1 Promise.resolve("one"); const promise2 Promise.resolve("two");Promise.all([promise1, promise2]).…...

腾讯云:数智教育专场-学习笔记
15点13分2024年10月21日(短短5天的时间,自己的成长速度更加惊人)-开始进行“降本增效”学习模式,根据小米手环对于自己的行为模式分析(不断地寻找数据之间的关联性),每天高效记忆时间࿰…...

Ovis: 多模态大语言模型的结构化嵌入对齐
论文题目:Ovis: Structural Embedding Alignment for Multimodal Large Language Model 论文地址:https://arxiv.org/pdf/2405.20797 github地址:https://github.com/AIDC-AI/Ovis/?tabreadme-ov-file 今天,我将分享一项重要的研…...

python的Django的render_to_string函数和render函数模板的使用
一、render_to_string render_to_string 是 Django 框架中的一个便捷函数,用于将模板渲染为字符串。 render_to_string(template_name.html, context, requestNone, usingNone) template_name.html:要渲染的模板文件的名称。context:传递给…...
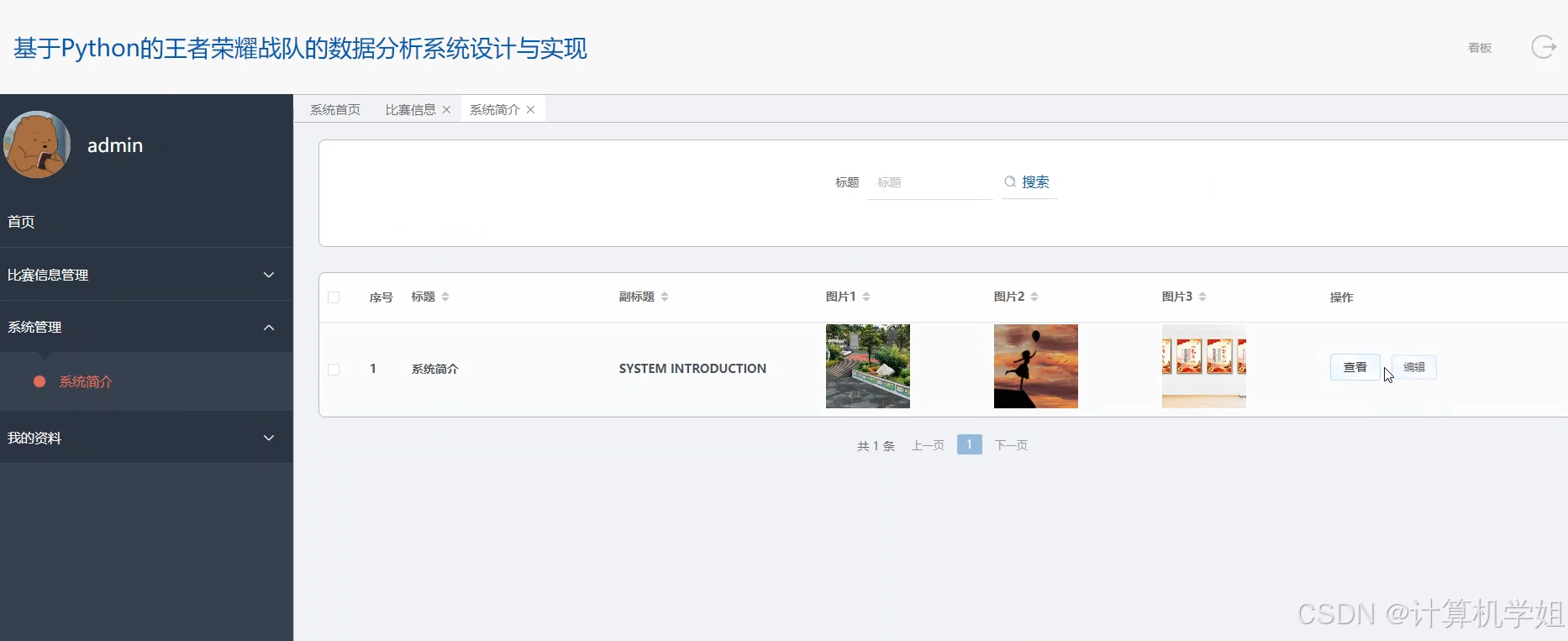
基于Python大数据的王者荣耀战队数据分析及可视化系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

【Linux学习】(3)Linux的基本指令操作
前言 配置Xshell登录远程服务器Linux的基本指令——man、cp、mv、alias&which、cat&more&less、head&tail、date、cal、find、grep、zip&tar、bc、unameLinux常用热键 一、配置Xshell登录远程服务器 以前我们登录使用指令: ssh 用户名你的公网…...

Mac 使用脚本批量导入 Apple 歌曲
最近呢,买了一个 iPad,虽然家里笔记本台式都有,显示器都是 2个,比较方便看代码(边打游戏边追剧)。 但是在床上拿笔记本始终还是不方便,手机在家看还是小了点,自从有 iPad 之后&…...

全桥PFC电路及MATLAB仿真
一、PFC电路原理概述 PFC全称“Power Factor Correction”(功率因数校正),PFC电路即能对功率因数进行校正,或者说是能提高功率因数的电路。是开关电源中很常见的电路。功率因数是用来描述电力系统中有功功率(实际使用…...
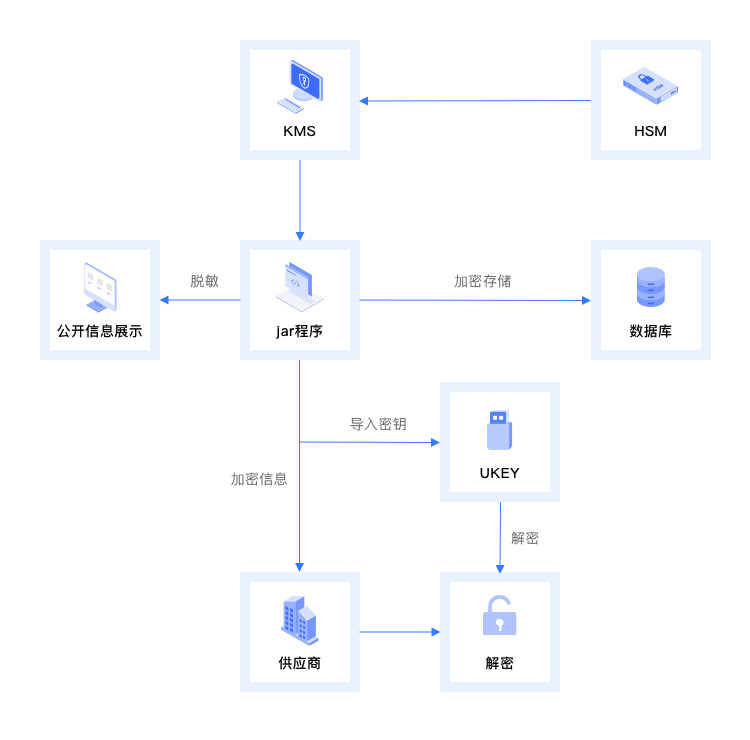
【安当产品应用案例100集】025-确保数据安全传输——基于KMS与HSM的定期分发加密解决方案
引言: 在当今快速发展的数字化时代,企业面临着前所未有的信息安全挑战。尤其是在需要向供应商定期分发敏感数据的情况下,如何保证这些数据在传输过程中的安全性变得至关重要。为此,我们推出了结合安当KMS密钥管理平台与HSM密码机…...

十 缺陷检测解决策略之三:频域+空域
十 缺陷检测解决策略之三:频域空域 read_image (Image, 矩形) * 中间低频,四周高频 fft_image (Image, ImageFFT) * 中间低频,四周高频 fft_generic (Image, ImageFFT1, to_freq, -1, sqrt, dc_center, complex) * 中间高频,四周低频 rft_ge…...

有望第一次走出慢牛
A股已走完30多年历程。 大约每十年,会经历一轮牛熊周期。特点是每一轮周期,大约九成的时间都是熊市主导。就是我们常说的 快牛慢熊。 这一次,会不会重复历史? 历史不会简单重复。已经感受到了盘面的变化。 有人说,股市爆涨爆…...
计算机网络(十二) —— 高级IO
#1024程序员节 | 征文# 目录 一,预备 1.1 重新理解IO 1.2 五种IO模型 1.3 非阻塞IO 二,select 2.1 关于select 2.2 select接口参数解释 2.3 timeval结构体和fd_set类型 2.4 socket就绪条件 2.5 select基本工作流程 2.6 简单select的服务器代…...

电力行业 | 等保测评(网络安全等级保护)工作全解
电力行业为什么要做网络安全等级保护? 电力行业是关系到国家安全和社会稳定的基础性行业,电力行业信息化程度相对较高,是首批国家信息安全等级保护的重点行业。 01 国家法律法规的要求 1994《计算机信息系统安全保护条例》(国务…...

总裁主题CeoMax-Pro主题7.6开心版
激活方式: 1.授权接口源码ceotheme-auth-api.zip搭建一个站点,绑定www.ceotheme.com域名,并配置任意一个域名的 SSL 证书。 2.在 hosts 中添加:127.0.0.1 www.ceotheme.com 3.上传class-wp-http.php到wp-includes目录ÿ…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
