数据结构之堆和二叉树的简介
1.树
1.1 树的概念与结构

注意:
1.树形结构中,子树之间不能有交集,否则就不是树形结构 !!!(相交了称为图,而不是树)
2.除了根结点外,每个结点有且仅有⼀个父结点
1.2 树相关术语

1.3 树的表示
struct TreeNode
{
struct Node* child; // 左边开始的第⼀个孩⼦结点
struct Node* brother; // 指向其右边的下⼀个兄弟结点
int data; // 结点中的数据域
};示例说明:


2. 二叉树
2.1 概念与结构


2.2 特殊的二叉树
2.2.1 满二叉树


💡 ⼆叉树性质
2.3 二叉树存储结构
2.3.1 顺序结构
2.3.2 链式结构
相关文章:

数据结构之堆和二叉树的简介
1.树 1.1 树的概念与结构 如图所示,树是⼀种非线性的数据结构,它是由 n (n>0) 个有限结点组成⼀个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 …...

微信小程序上传图片添加水印
微信小程序使用wx.chooseMedia拍摄或从手机相册中选择图片并添加水印, 代码如下: // WXML代码:<canvas canvas-id"watermarkCanvas" style"width: {{canvasWidth}}px; height: {{canvasHeight}}px;"></canvas&…...

xshell5找不到匹配的host key算法
xshell5找不到匹配的host key算法,是因为电脑客户端不支持服务器的算法,因此需要再服务器增加算法。 下面以Ubuntu系统为例,修改下面的文件 sudo vim /etc/ssh/sshd_config 增加下面算法 KexAlgorithms diffie-hellman-group-exchange-…...

Linux中安装Tomcat
文章目录 一、Tomcat介绍1.1、Tomcat是什么1.2、Tomcat的工作原理1.3、Tomcat适用的场景1.4、Tomcat与Nginx、Apache比较1.4.1、优势1.4.2、劣势1.4.3、定位功能 1.5、Tomcat 的主要组件1.6、Tomcat 的主要配置文件 二、Tomcat安装2.1、查看可用的JDK2.2、安装OpenJDK 112.3、配…...

RV1126音视频学习(二)-----VI模块
文章目录 前言2.RV1126的视频输入vi模块2.1什么是VI模块2.3RV1126VI模块主要APIRK_MPI_SYS_Init()RK_MPI_VI_SetChnAttrRK_MPI_VI_EnableChnRK_S32 RK_MPI_VI_DisableChnRK_MPI_VI_StartStreamRK_MPI_SYS_GetMediaBufferRK_MPI_MB_GetPtrRK_MPI_MB_GetSizeRK_MPI_MB_ReleaseBuf…...

「C/C++」C++17 之 std::string_view 轻量级字符串视图
✨博客主页何曾参静谧的博客📌文章专栏「C/C」C/C程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasoli…...
Linux内核-内核模块内核参数
作者介绍:简历上没有一个精通的运维工程师。希望大家多多关注作者,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 我们的Linux进阶部分,到目前为止,已经讲过:硬件,日常运维,基础软…...
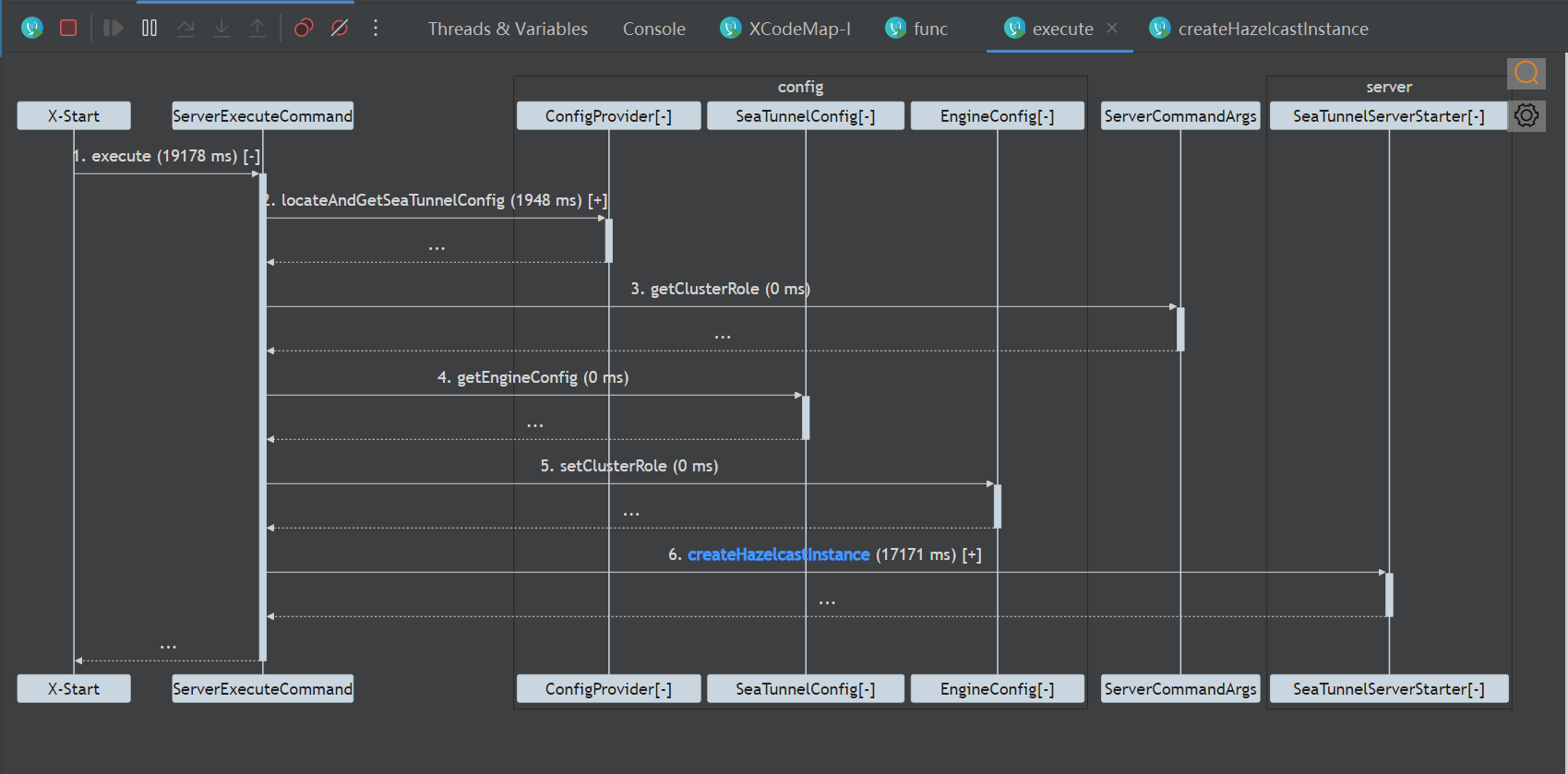
中电信翼康工程师:我在 Apache SeaTunnel 社区的贡献之旅
贡献者Github ID:luckyLJY 文章整理:曾辉 Apache SeaTunnel 作为一款强大的数据同步和转换工具,凭借其部署易用性、容错机制、数据源支持、性能优势、功能丰富性以及活跃的社区支持,成为了数据工程师们不可或缺的利器。 因其具有的…...

【ESP32S3】VSCode 开发环境搭建
ESP32S3 有多种开发方式,主流的有 Eclipse 和 VSCode 两种。本文来介绍一下基于 VSCode 的开发环境搭建。 VSCode 环境需要依赖于 ESP-IDF 插件,因此需要在 VSCode 插件市场中搜索并安装 ESP-IDF 插件: 安装完成后侧边栏会多出一个 ESP-IDF …...

大模型,多模态大模型面试问题基础记录24/10/24
大模型,多模态大模型面试问题基础记录24/10/24 问题一:LoRA是用在节省资源的场景下,那么LoRA具体是节省了内存带宽还是显存呢?问题二:假如用pytorch完成一个分类任务,那么具体的流程是怎么样的?…...

使用TimeShift备份和恢复Ubuntu Linux
您是否曾经想过如何备份和恢复您的Ubuntu或Debian系统?TimeShift是一个强大的备份和还原工具。TimeShift允许您创建系统快照,提供了一种在出现意外问题或系统故障时恢复到先前状态的简便方式。您可以使用RSYNC或BTRFS创建快照。 有了这个介绍࿰…...
win7现在还能用吗_哪些配置的电脑还可以安装win7系统
2024年了都,win7现在还能用吗?答案是肯定的。那么哪些配置的电脑还可以安装win7系统呢?下面就针对这两个问题详细分区。 win7现在还能用吗? Windows 7系统虽然已经停止官方支持,但仍然可以使用。以下是关于Windows 7系…...

基于GPT的智能客服落地实践
📍前言 在日常生活中,「客服」这个角色几乎贯穿着我们生活的方方面面。比如,淘宝买东西时,需要客服帮你解答疑惑。快递丢失时,需要客服帮忙找回。报名参加培训课程时,需要客服帮忙解答更适合的课程…… 基…...

Sourcetree和GitLab的结合使用
一、写在前面 为什么是Sourcetree和GitLab?因为遇到的坑最少,在不用梯子的情况下,推送速度还可以。 这篇文章主要介绍的是,怎么把自己写的代码文件打包放到GitLab上去,方便别人下载使用,也方便自己在另一…...

双十一开启极速达夜派;黑神话获泰国年度最佳游戏;AI 模型可帮助识别 17000 多种疾病的候选药物....| 网易数智日报
双 11 菜鸟在北京、上海、广州、杭州等城市开启「预售极速达夜派」服务 10 月 21 日,菜鸟在北京、上海、广州、杭州等城市开启「预售极速达夜派」服务,批量大促包裹实现小时级送达。 据介绍,在消费者支付尾款前,菜鸟供应链就已经…...

深入理解JAVA虚拟机(一)
介绍JAVA虚拟机的运行时数据区域 按照物理结构来划分:java虚拟机主要由以下几部分构成栈、堆和程序计数器,其中栈又可以分为虚拟机栈VM stack 和 本地方法栈 Native Method Statck,堆可以划分方法区和普通的堆内存。按照逻辑划分线程私有空间…...

从Excel文件中读取数据
笔记 import openpyxl # 打开工作簿 workbookopenpyxl.load_workbook(景区天气.xlsx) # 选择要操作的工作表 sheetworkbook[景区天气] # 表格数据是二维列表,先遍历的是行,后遍历的是列 lst[] # 存储的是行数据 for row in sheet.rows:sublst[] # 存储单…...

深入剖析MySQL的索引机制及其选型
在数据库管理系统中,索引是一种重要的优化工具,用于加速数据的检索和查询处理。在MySQL中,合理使用索引可以显著提高数据库的性能。本文将深入探讨MySQL的索引机制,包括不同类型索引的优势、劣势及在实际使用中的选型策略。 1. 什…...
校园表白墙源码修复版
此校园表白墙源码基于thinkphp,因为时代久远有不少bug,经本人修复已去除大部分bug,添加了美化元素。 https://pan.quark.cn/s/1f9b3564c84b https://pan.baidu.com/s/1bb9vu9VV2jJoo9-GF6W3xw?pwd7293 https://caiyun.139.com/m/i?2hoTc…...

Android 内存优化——常见内存泄露及优化方案
看到了一篇关于内存泄漏的文章后,就想着分享给大家,最后一起学习,一起进步: 如果一个无用对象(不需要再使用的对象)仍然被其他对象持有引用,造成该对象无法被系统回收,以致该对象在…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
