当前位置： 首页 > news >正文

西南大学软件专硕考研难度分析！

news 2026/2/7 22:27:41

 C哥专业提供——计软考研院校选择分析+专业课备考指南规划

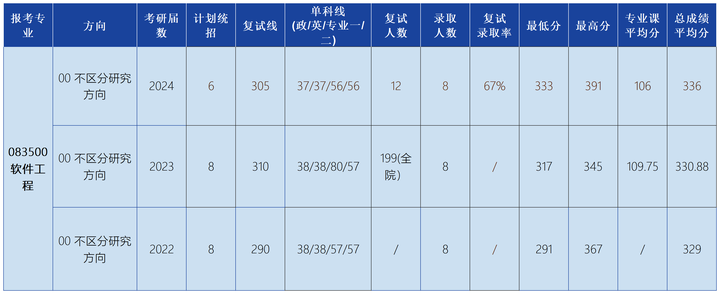
西南大学软件工程学硕近三年呈现出招生规模稳定、复试线稳中有升的特点。2024届实际录取8人，复试分数线305分，复试录取率67%，相比去年复试线略有下降但仍高于2022届，显示出温和的竞争态势。

详细分析

1. 统招录取人数分析

2022-2024届实际录取人数均为8人，计划招生6-8人之间波动：

  • 2024届：计划6人，实际录取8人，扩招明显

  • 2023届：计划8人，实际录取8人

  • 2022届：计划8人，实际录取8人

趋势预测：2025届计划招生大概率维持在6-8人区间，且仍有扩招可能。

2. 复试分数线分析

近三年复试线变化：

  • 2024届：305分

  • 2023届：310分

  • 2022届：290分

复试线呈现"稳中有升"趋势，但2024届略有回落，显示专业难度趋于平稳。

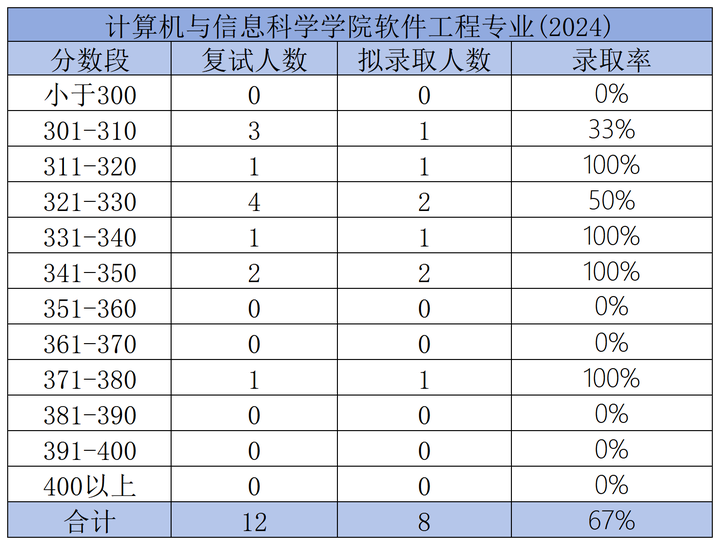
3. 录取分数分布分析（2024届）

  • 390分以上：1人，录取率100%

  • 331-350分：3人，录取率100%

  • 321-330分：2人，录取率50%

  • 311-320分：1人，录取率100%

  • 301-310分：1人，录取率33%

值得注意的是：

  • 分数分布相对分散，跨度较大（310-391分）

  • "过线就有机会录取"特征明显

  • 稳定录取线约在330分左右（录取率接近60%的分数段）

2025届报考建议

1. 报考难度预测

基于近三年数据和考研大环境变化，2025届"大概率稳定，小概率升"：

  • 复试分数线预计在305-315分之间

  • 统招人数可能维持在8人左右

  • 扩招可能性较大

2. 建议目标分数

  • 保底线：310分

  • 稳定录取线：330分+

  • 绝对安全线：350分+

3. 报考性价比分析

西南大学软件工程学硕具有以下优势：

  1. 双一流院校品牌

  2. 较低的录取分数要求

  3. "过线即有机会"的特点

  4. 稳定的扩招趋势

综合来看，该专业在2025届"依然具备性价比，值得报考"。建议：

  1. 优先考虑：适合英语数学基础扎实、专业课有把握的考生

  2. 择优备选：可作为985/211计算机类考生的保底院校

  3. "抄底"机会：适合想考双一流但分数实力暂时不够的考生

4. 重要提醒

  1. 复试比例较高，建议考生在准备初试的同时也要重视复试

  2. 专业课分数要求不高，可适当将精力向公共课倾斜

  3. 建议密切关注2025届具体招生计划，尤其是招生人数变化

总体而言，西南大学软件工程学硕是2025届考研"性价比较高"的选择，尤其适合想考双一流但担心高分门槛的考生。

希望C哥的文章能够帮到大家更清晰明了计算机软件的考研院校选择解决考研相关问题；

需计软考研院校选择规划及备考指南，欢迎找C哥唠嗑儿~

也祝大家都能金榜题名，一战上岸！

希望C哥的文章能够帮到大家更清晰明了计算机软件的考研院校选择解决考研相关问题；

需计软考研院校选择规划及备考指南，欢迎找C哥唠嗑儿~

也祝大家都能金榜题名，一战上岸！

相关文章：

西南大学软件专硕考研难度分析！

C哥专业提供——计软考研院校选择分析专业课备考指南规划 西南大学软件工程学硕近三年呈现出招生规模稳定、复试线稳中有升的特点。2024届实际录取8人，复试分数线305分，复试录取率67%，相比去年复试线略有下降但仍高于2022届，显示出…...

编程日记 2024/10/28 0:19:05

计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-21

计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-21 目录 文章目录 计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-21目录1. The Fair Language Model Paradox摘要研究背景问题与挑战如何解决创新点算法模型实验效果重要数据与结论推荐阅读指数&…...

编程日记 2024/10/28 0:18:04

安全芯片 OPTIGA TRUST M 使用介绍与示例（基于STM32裸机）

文章目录 目的资料索引硬件电路软件框架介绍数据存储框架移植框架使用 使用示例示例地址与硬件连接通讯测试功能测试 总结 目的 OPTIGA TRUST M 是英飞凌推出的安全芯片，芯片通提供了很多 slot ，用于存放各类安全证书、密钥、用户数据等，内置…...

编程日记 2024/10/28 0:17:03

【AI换装整合及教程】CatVTON：时尚与科技的完美融合

在当今数字化时代，时尚行业正经历着一场前所未有的变革，而 CatVTON 作为一款由中山大学、Pixocial 等机构联合研发的轻量化 AI 虚拟换装工具，无疑是这场变革中的璀璨明星。 一、独特的技术架构 CatVTON 基于 Stable Diffusion v1.5 inpainit…...

编程日记 2024/10/28 0:15:01

接口测试（七）jmeter——参数化（RandomString函数）

一、RandomString函数 需求：模拟10个用户注册 1. 【工具】–>【函数助手对话框】 2. 选择RandomString函数 假设手机号码前3位设置为固定数值136，后8位可用RandomString函数随机产生数值 ① Random string length：8（随机长度…...

编程日记 2024/10/28 0:14:00

simple_php

访问靶场 这里传入a和b参数，绕过三个if即可拿到flag a a a_GET[ a’ ];中是抑制报错信息的。 第一个if非常的抽象， if($a0 and $a){echo $flag1; }处理a 要输出flag1,a0，但是，在php中0被视为假也就是Flase 如果a0&#xff0…...

编程日记 2024/10/28 0:12:59

网络搜索引擎Shodan（4）

声明：学习视频来自b站up主 泷羽sec，如涉及侵权马上删除文章 声明：本文主要用作技术分享，所有内容仅供参考。任何使用或依赖于本文信息所造成的法律后果均与本人无关。请读者自行判断风险，并遵循相关法律法规。 感谢泷…...

编程日记 2024/10/28 0:11:58

【Flask】一、安装与第一个测试程序

目录 Flask简介 安装Flask 安装pip（Python包管理器） 使用pip安装Flask 验证安装 创建Flask程序 创建应用 运行 访问测试 Flask简介 Flask是一个用Python编写的轻量级Web应用框架。它被设计为易于使用和扩展，使其成为构建简单网站或复…...

编程日记 2024/10/28 0:10:56

R语言笔记（二）：向量

文章目录 一、Data structure: vectors二、Indexing vectors三、Re-assign values to vector elements四、Generic function for vectors五、Vector of random samples from a distribution六、Vector arithmetic七、Recycling八、Element-wise comparisons of vectors九、Comp…...

编程日记 2024/10/28 0:09:55

信息安全工程师（71）隐私保护技术与应用

前言 隐私保护技术是指通过一系列的技术手段来保护人们的隐私不被公开泄露。随着数字化和网络化社会的发展，个人隐私的保护变得尤为重要，隐私保护技术也因此得到了广泛的应用和发展。 一、隐私保护技术概述 隐私保护技术主要包括数据加密技术、身份认证技…...

编程日记 2024/10/28 0:04:51

层和块学习

1.生成一个网络，其中包含一个具有256个单元和ReLU激活函数的全连接隐藏层，然后是一个具有10个隐藏单元且不带激活函数的全连接输出层。 import torch from torch import nn from torch.nn import functional as Fnet nn.Sequential(nn.Linear(20, 256)…...

编程日记 2024/10/28 0:03:50

Zookeeper面试整理-源码及实现细节

Zookeeper 的源码和实现细节是理解其高可用性、分布式一致性和高效性的关键。以下是 Zookeeper 的核心实现细节，涵盖其架构、关键模块、以及具体的代码实现机制。 1. Zookeeper 架构 Zookeeper 采用 Leader-Follower 架构，集群由多个节点组成。主要分为三种角色：Leader、Fol…...

编程日记 2024/10/28 0:01:48

岭回归的MATLAB步骤

MATLAB 实现框架，它涵盖了从数据导入到岭回归的步骤，包括计算共线性、使用 MAE、MSE、R、MAPE 进行评价，以及绘制相应的可视化图表。 1. 数据导入 首先，导入你的 Excel 文件 data.xlsx。假设前面的列是因变量（特征&a…...

编程日记 2024/10/28 0:00:47

智能指针(unique_ptr，shared_ptr，weak_ptr)

在实际的C开发中，我们经常会遇到诸如程序运行中突然崩溃，程序运行所用内存越来越多最终不得不重启等问题，这些问题往往都是内存资源管理不当造成的(内存泄漏) 比如： 有些内存资源已经被释放，但指向它的指针并没有改变指…...

编程日记 2024/10/27 23:59:45

Sql执行较慢的排查方式

SQL执行较慢的排查方式涉及多个方面，包括检查SQL语句本身、数据库配置、硬件资源等。以下是一些具体的排查步骤和优化建议： 一、检查SQL语句 启用慢查询日志： 大多数数据库管理系统（如MySQL、PostgreSQL）都支持慢查询…...

编程日记 2024/10/27 23:58:44

CesiumJS 案例 P6：添加图片图层、添加图片图层并覆盖指定区域

CesiumJS CesiumJS API&#xff1a;https://cesium.com/learn/cesiumjs/ref-doc/index.html CesiumJS 是一个开源的 JavaScript 库&#xff0c;它用于在网页中创建和控制 3D 地球仪&#xff08;地图&#xff09; 一、添加图片图层 <!DOCTYPE html> <html lang"…...

编程日记 2024/10/27 23:56:41

Python画笔案例-094 绘制 神奇彩条动画

1、绘制 神奇彩条动画 通过 python 的turtle 库绘制 神奇彩条动画，如下图： 2、实现代码 绘制 神奇彩条动画，以下为实现代码： """神奇彩条动画.py一个用海龟画图的图章功能配合颜色渐变和动画原理做成的动画。 """ from random import randi…...

编程日记 2024/10/27 23:55:40

javaScript整数反转

function _reverse(number) { // 补全代码 return (number ).split().reverse().join(); } number &#xff1a;首先&#xff0c;将数字 number 转换为字符串。在 JavaScript 中&#xff0c;当你将一个数字与一个字符串相加时&#xff0c;JavaScript 会自动将数字转换为字符串…...

编程日记 2024/10/27 23:54:39

Zookeeper面试整理-故障排查和调试

在使用 Zookeeper 的过程中，可能会遇到各种问题，如性能下降、节点失效、集群不可用等。为了保持系统的稳定性和高可用性，掌握 Zookeeper 的故障排查和调试方法至关重要。以下是一些常见的故障排查技巧和调试方法： 1. 日志分析 Zookeeper 的日志是最直接的调试和故障排查工具…...

编程日记 2024/10/27 23:53:38

PG数据库之索引详解

PostgreSQL数据库中的索引是一种用于提高查询性能的重要数据结构。通过索引&#xff0c;数据库可以快速定位到表中的特定行&#xff0c;而无需进行全表扫描。PostgreSQL支持多种索引类型&#xff0c;每种类型都有其特定的应用场景和性能特点。下面将详细介绍PostgreSQL中的索引…...

编程日记 2024/10/27 23:51:36

【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验

系列回顾&#xff1a; 在上一篇中&#xff0c;我们成功地为应用集成了数据库&#xff0c;并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了&#xff01;但是&#xff0c;如果你仔细审视那些 API&#xff0c;会发现它们还很“粗糙”&#xff1a;有…...

编程新知 2026/1/22 20:46:43

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2026/1/27 18:13:23

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...

编程新知 2025/11/25 19:50:27

Webpack性能优化：构建速度与体积优化策略

一、构建速度优化 1、​​升级Webpack和Node.js​​ ​​优化效果​​&#xff1a;Webpack 4比Webpack 3构建时间降低60%-98%。​​原因​​&#xff1a; V8引擎优化&#xff08;for of替代forEach、Map/Set替代Object&#xff09;。默认使用更快的md4哈希算法。AST直接从Loa…...

编程新知 2025/12/26 15:05:09

基于PHP的连锁酒店管理系统

有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发&#xff0c;数据库mysql&#xff0c;前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

编程新知 2026/1/31 6:20:15

Kafka主题运维全指南：从基础配置到故障处理

#作者&#xff1a;张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1&#xff1a;主题删除失败。常见错误2&#xff1a;__consumer_offsets占用太多的磁盘。 主题日常管理 …...

编程新知 2025/6/10 21:14:43

LangChain 中的文档加载器（Loader）与文本切分器（Splitter）详解《二》

&#x1f9e0; LangChain 中 TextSplitter 的使用详解&#xff1a;从基础到进阶&#xff08;附代码&#xff09; 一、前言 在处理大规模文本数据时&#xff0c;特别是在构建知识库或进行大模型训练与推理时&#xff0c;文本切分&#xff08;Text Splitting&#xff09; 是一个…...

编程新知 2025/10/10 9:24:44

rm视觉学习1-自瞄部分

首先先感谢中南大学的开源&#xff0c;提供了很全面的思路&#xff0c;减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接&#xff1a;https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架&#xff1a; 代码框架结构&#xff1a;readme有…...

编程新知 2026/2/7 21:45:37

React核心概念：State是什么？如何用useState管理组件自己的数据？

系列回顾&#xff1a; 在上一篇《React入门第一步》中&#xff0c;我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目&#xff0c;并修改了App.jsx组件&#xff0c;让页面显示出我们想要的文字。但是&#xff0c;那个页面是“死”的&#xff0c;它只是静态…...

编程新知 2025/11/3 8:29:51

RLHF vs RLVR：对齐学习中的两种强化方式详解

在语言模型对齐&#xff08;alignment&#xff09;中&#xff0c;强化学习&#xff08;RL&#xff09;是一种重要的策略。而其中两种典型形式——RLHF&#xff08;Reinforcement Learning with Human Feedback&#xff09; 与 RLVR&#xff08;Reinforcement Learning with Ver…...

编程新知 2026/1/15 4:23:13