当前位置： 首页 > news >正文

matlab线性度计算程序

news 2026/2/7 6:48:17

matlab线性度计算程序

环境

matlab2023a
ads2020

原理

其中f(v)是曲线，fmax是f(v)的最大值，fmin是f(v)的最小值，vmax为fmax对应v值，vmin为fmin对应v值。
L=∆fmax/(fmax-fmin) (1)
∆fmax=max⁡[f(v)-[fmin-K*(v-vmin)]] (2)
K=(fmax-fmin)/(vmax-vmin) (3)

代码

data1=importdata('schematic24.txt');%改变输入的文件名，文件数据的格式不一致需要自己调节
data2=data1.data; 
vt=data2(:,1); %X轴的数据  若不要前十个数据==》vt=data2(10:end,1); 若全部==》改为  vt=data2(:,1);
freq=data2(:,2); %Y轴的数据 若不要前十个数据==》freq=data2(10:end,2); 若全部==》改为  freq=data2(:,2);
vt1=min(vt):0.05:max(vt);
freq1=interp1(vt,freq,vt1,"linear");K=(max(freq1)-min(freq1))/(max(vt1)-min(vt1));
DeltaFreq=abs(freq1-(min(freq1)+K.*(vt1-min(vt1))));
DeltaFreqMax=max(DeltaFreq);
L=DeltaFreqMax/(max(freq1)-min(freq1));%线性度IdealCurve=(min(freq1)+K.*(vt1-min(vt1)));
plot(vt1,freq1,vt1,IdealCurve);
xlabel("Vt(V)");
ylabel("F(GHz)");
RelativeBandwidth=(max(freq1)-min(freq1))/(max(freq1)+min(freq1))*2;

输入数据

ads导出的Vt-f数据

Vt	f
4.00000000000000000E0	9.94315915744877721E-1
4.25000000000000000E0	1.01493151204090859E0
4.50000000000000000E0	1.03422490807067180E0
4.75000000000000000E0	1.05164280768404428E0
5.00000000000000000E0	1.06777990432062753E0
5.25000000000000000E0	1.08310328336644468E0
5.50000000000000000E0	1.09770768003155950E0
5.75000000000000000E0	1.11172932575729133E0
6.00000000000000000E0	1.12531380108596224E0
6.25000000000000000E0	1.13860792898479035E0
6.50000000000000000E0	1.15175718538421945E0
6.75000000000000000E0	1.16490578392067912E0
7.00000000000000000E0	1.17819886343963476E0
7.25000000000000000E0	1.19178584077378091E0
7.50000000000000000E0	1.20582289238475937E0
7.75000000000000000E0	1.22047052795578836E0
8.00000000000000000E0	1.23587824306338967E0
8.25000000000000000E0	1.25213803071271568E0
8.50000000000000000E0	1.26913562979576611E0
8.75000000000000000E0	1.28555359654201840E0
9.00000000000000000E0	1.30713158672056151E0
9.25000000000000000E0	1.32704294998017724E0
9.50000000000000000E0	1.34599061749011306E0
9.75000000000000000E0	1.36427848181836309E0
1.00000000000000000E1	1.38159593690375027E0

结果

在这里插入图片描述
在这里插入图片描述
可以看到线性度为4.29%。

相关文章：

matlab线性度计算程序

matlab线性度计算程序 环境 matlab2023a ads2020 原理 其中f(v)是曲线，fmax是f(v)的最大值，fmin是f(v)的最小值，vmax为fmax对应v值，vmin为fmin对应v值。 L∆fmax/(fmax-fmin) (1) ∆fmaxmax⁡[f(v)-[fmin-K*(v-vmin)]] (2) K(…...

编程日记 2024/10/31 23:26:28

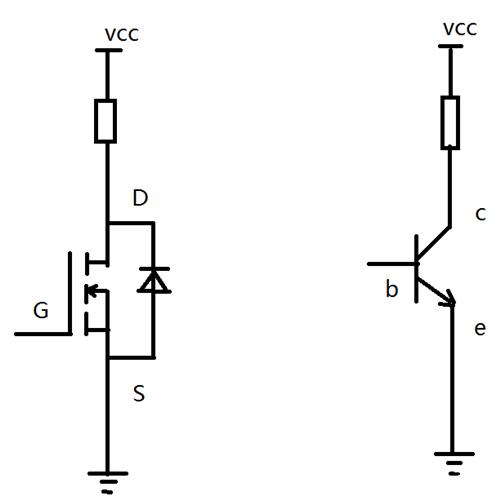
为什么NMOS管比PMOS管更受欢迎？

NMOS在实际应用中为何比PMOS要更受欢迎。本文将从导电沟道、电子迁移率和器件速度等多个方面来展开讲解。 首先是在性能方面考虑： 与NMOS管驱动能力相同的一个PMOS管，其器件面积可能是NMOS管的2～3倍，然而器件面积会影响导通电阻…...

编程日记 2024/10/31 23:24:27

【论文复现】短期电力负荷

作者主页： 七七的个人主页 文章收录专栏： 论文复现 欢迎大家点赞 👍 收藏 ⭐ 加关注哦！💖💖 短期电力负荷 论文发表问题背景一. 基本问题二. 本论文发现的问题 对于论文发现问题的解决方案：复现…...

编程日记 2024/10/31 23:23:25

pytest脚本常用的执行命令

pytest脚本常用的执行命令 一、一般执行的脚本，执行.py文件整个脚本二、执行.py文件脚本中的一个模块三、执行脚本，执行.py文件整个脚本，或则一个模块，查看对应的日志信息3.1.py文件执行allure的脚本3.2去dos框下去执行对应的脚本…...

编程日记 2024/10/31 23:18:20

OpenCv入门

一.OpenCv简介 1 图像的起源 1.1图像是什么？ 图：是物体反射或透射光的分布 像：是人的视觉系统所接受的图在人脑中所形版的印象或认识 1.2模拟图像和数字图像 模拟图像：连续存储的图像 数字图像：分级存储的图像 2 数字…...

编程日记 2024/10/31 23:17:19

超详细的flex教程（面试必考）

引言 为什么存在？ Flex 布局的出现是为了解决传统 CSS 布局方式（如浮动布局、定位布局等）在处理复杂布局时的诸多限制和不便。 优势 1. 简化布局 Flex 布局的语法简洁明了，代码更易读。 2. 强大的对齐能力 提供丰富的对齐属…...

编程日记 2024/10/31 23:16:18

C++的输入与输出

一.格式和注意要点 1. #include<iostream>; using namespace std; 标准库定义了4个IO对象&#xff0c;IO(输入输出)&#xff0c;以下&#xff1a; cin是一个istream流对象&#xff0c;现在理解为标准输入即可。cout是一个ostream流对象&#xff0c;理解为标准输出即可。…...

编程日记 2024/10/31 23:12:13

上海剧某文化传播有限公司与喜某（上海）网络科技有限公司、上海喜某科技有限公司侵害著作权及不正当竞争纠纷案

上海剧某文化传播有限公司与喜某&#xff08;上海&#xff09;网络科技有限公司、上海喜某科技有限公司侵害著作权及不正当竞争纠纷案的详细情况如下&#xff1a; 基本案情&#xff1a; 上海剧某文化传播有限公司&#xff08;以下简称剧某公司&#xff09;是电视剧《宸汐缘》的…...

编程日记 2024/10/31 23:08:10

【c++篇】：模拟实现string类--探索字符串操作的底层逻辑

✨感谢您阅读本篇文章&#xff0c;文章内容是个人学习笔记的整理&#xff0c;如果哪里有误的话还请您指正噢✨ ✨ 个人主页&#xff1a;余辉zmh–CSDN博客 ✨文章所属专栏&#xff1a;c篇–CSDN博客 文章目录 前言一.string类的默认成员函数以及深拷贝1.基本框架2.默认成员函数…...

编程日记 2024/10/31 23:06:06

springboot配置logback.xml遇到的几个问题

最近项目用到对日志脱敏&#xff0c;经过研究通过logback实现了对日志脱敏&#xff0c;上篇文章中详细讲解了如果配置。但是还是对logback的配置不太了解。比如springboot怎么加载这个logback.xml的。 首先&#xff0c;默认情况下&#xff0c;logback.xml文件是放在类目录下&am…...

编程日记 2024/10/31 23:05:05

MySQL 5.7与MySQL 8.0对比

一、功能对比 JSON支持 MySQL 5.7&#xff1a;引入了JSON数据类型&#xff0c;允许用户存储和操作JSON格式的数据&#xff0c;这是NoSQL功能的一个重要补充。但相对于MySQL 8.0&#xff0c;其功能和性能较弱。MySQL 8.0&#xff1a;在JSON支持方面进行了重大改进&#xff0c;引…...

编程日记 2024/10/31 23:04:05

【代码随想录Day55】图论Part07

prim 算法精讲 题目链接/文章讲解&#xff1a;代码随想录 import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner new Scanner(System.in);// 读取顶点数和边数int vertexCount scanner.nextInt();int edgeCount scanner.nextI…...

编程日记 2024/10/31 23:03:04

软考在即!这些注意事项你提前了解！

11月软考马上就要开始了&#xff0c;但是&#xff0c;还有很多的考生&#xff0c;可能还不知道自己到底应该去了解些什么&#xff1f;本文将详细介绍机考注意事项及系统操作提示&#xff0c;帮助考生们备考无忧。 一、考试入场要求和考场规则 1、入场时间&#xff1a;考生需提…...

编程日记 2024/10/31 23:02:02

CMake知识点

参考&#xff1a; https://zhuanlan.zhihu.com/p/661284252 cmake使用教程&#xff08;实操版&#xff09;-CSDN博客 【CMake】CMake从入门到实战系列&#xff08;二&#xff09;——实例入手&#xff0c;讲解CMake的基本流程_cmake创建一个可执行目标的过程-CSDN博客 一、…...

编程日记 2024/10/31 23:01:02

git ls-remote

文章目录 1.简介2.格式3.选项4.示例5.小结参考文献 1.简介 git ls-remote 是一个 Git 命令&#xff0c;用于列出远程 Git 仓库的引用&#xff08;refs&#xff09;&#xff0c;包括分支、标签等。 这个命令非常有用&#xff0c;可以帮助你查看远程仓库中可用的分支和标签&…...

编程日记 2024/10/31 23:00:01

低代码平台如何通过AI赋能，实现更智能的业务自动化？

引言 随着数字化转型的加速推进&#xff0c;企业在日常运营中面临的业务复杂性与日俱增。如何快速响应市场需求&#xff0c;优化流程&#xff0c;并降低开发成本&#xff0c;成为各行业共同关注的核心问题。低代码平台作为一种能够快速构建应用程序的工具&#xff0c;因其可视化…...

编程日记 2024/10/31 22:58:59

计算疫情扩散时间

该专栏题目包含两部分&#xff1a; 100 分值部分题目 200 分值部分题目 所有题目都会陆续更新&#xff0c;订阅防丢失 题目描述 在一个地图中(地图由 N ∗ N N*N N∗N 个区域组成)&#xff0c;有部分区域被感染病菌。 感染区域每天都会把周围(上下左右)的4个区域感染。 请…...

编程日记 2024/10/31 22:50:47

【Windows11】24H2 内存占用高（截至10月31日）

文章目录 一、问题二、解决三、原因 一、问题 系统版本&#xff1a; 内存只有32GB。 以前只有我在运行数据处理程序的时候内存占用才会很高&#xff0c;日常情况下应该只有40%、50%左右的。 但是24H2&#xff0c;日常情况下内存占用80%以上。 而我只开了很少的应用&#…...

编程日记 2024/10/31 22:45:42

题目：多个字符从两端移动，向中间汇聚

【多个字符从两端移动&#xff0c;向中间汇聚】 char arr1[] "Good Good Study,Day Day Up!" ; char arr2[] "***************************"; 【思路】 首先两字符串中的元素个数要相同&#xff0c;将两串字符分别存放在数组中&#xff0c;那么字符串中…...

编程日记 2024/10/31 22:43:40

前端如何安全存储密钥，防止信息泄露

场景 把公钥硬编码在前端代码文件里&#xff0c;被公司安全检测到了要整改&#xff0c;于是整理几种常见的前端密钥存储方案。 1. 设置环境变量再读取 在打包或部署前端应用时&#xff0c;可以将密钥配置为环境变量&#xff0c;在应用运行时通过环境变量读取密钥。这样可以将密…...

编程日记 2024/10/31 22:42:39

Spark 之 入门讲解详细版（1）

1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室&#xff08;Algorithms, Machines, and People Lab&#xff09;开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目&#xff0c;8个月后成为Apache顶级项目&#xff0c;速度之快足见过人之处&…...

编程新知 2026/2/5 4:17:31

【入坑系列】TiDB 强制索引在不同库下不生效问题

文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1：执行计划绑定问题？尝试：SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库，并对 SQL 进行优化了，添加了强制索引。 UAT 环境已经生效，但 PROD 环境强制索…...

编程新知 2026/1/31 21:56:58

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2026/1/31 6:04:01

Nginx server_name 配置说明

Nginx 是一个高性能的反向代理和负载均衡服务器&#xff0c;其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机&#xff08;Virtual Host&#xff09;。 1. 简介 Nginx 使用 server_name 指令来确定…...

编程新知 2025/9/6 16:47:17

EtherNet/IP转DeviceNet协议网关详解

一&#xff0c;设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络&#xff0c;本网关连接到EtherNet/IP总线中做为从站使用&#xff0c;连接到DeviceNet总线中做为从站使用。 在自动…...

编程新知 2026/1/31 6:53:51

【OSG学习笔记】Day 16: 骨骼动画与蒙皮（osgAnimation）

骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术&#xff0c;它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton)&#xff1a;由层级结构的骨头组成&#xff0c;类似于人体骨骼蒙皮 (Mesh Skinning)&#xff1a;将模型网格顶点绑定到骨骼上&#xff0c;使骨骼移动…...

编程新知 2026/2/1 5:42:50

RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程

本文较长&#xff0c;建议点赞收藏&#xff0c;以免遗失。更多AI大模型应用开发学习视频及资料&#xff0c;尽在聚客AI学院。 本文全面剖析RNN核心原理&#xff0c;深入讲解梯度消失/爆炸问题&#xff0c;并通过LSTM/GRU结构实现解决方案&#xff0c;提供时间序列预测和文本生成…...

编程新知 2026/1/20 17:16:46

MinIO Docker 部署：仅开放一个端口

MinIO Docker 部署：仅开放一个端口 在实际的服务器部署中，出于安全和管理的考虑，我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务，支持 Docker 部署，但默认情况下它需要两个端口：一个是 API 端口（用于存储和访问数据），另一个是控制台端口（用于管理界面…...

编程新知 2025/12/23 11:08:56

第7篇：中间件全链路监控与 SQL 性能分析实践

7.1 章节导读 在构建数据库中间件的过程中&#xff0c;可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中&#xff0c;必须做到&#xff1a; &#x1f50d; 追踪每一条 SQL 的生命周期&#xff08;从入口到数据库执行&#xff09;&#…...

编程新知 2025/12/11 0:27:15

解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist

现象&#xff1a; android studio报错&#xff1a; [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决&#xff1a; 不要动CMakeLists.…...

编程新知 2025/12/15 0:46:42