动态规划 —— 路径问题-下降路径最小和
1. 下降路径最小和
题目链接:
931. 下降路径最小和 - 力扣(LeetCode)
https://leetcode.cn/problems/minimum-falling-path-sum/description/



2. 算法原理
状态表示:以莫一个位置位置为结尾
dp[i,j]表示:到达[i,j]位置的时候,此时的最小下降路径
2. 状态转移方程
根据最近的一步来划分问题:
以最小的下降路径到达A位置,然后再走一步到达目的地
到达dp[i][j]有三种情况:
1. 从左上方位置过来:[i-1,j-1] -> [i,j],dp[i-1,j-1] + m[i][j]
(缩写为x)
2. 从正上方位置过来:[i-1,j] -> [i,j],dp[i-1,j] + m[i][j]
(缩写为y)
3. 从右上方位置过来:[i-1,j+1] -> [i,j],dp[i-1,j+1] + m[i][j]
(缩写为z)
本题的状态转移方程是:dp[i][j] = min(x,y,z)+m[i][j]
3. 初始化 :把dp表填满不越界,让后面的填表可以顺利进行
我们可以在上面的一行和左边还有右边的一列再额外的加上一行和两列的虚拟节点
原始矩阵里第一行的值是不能被改变的,不然会影响到最终结果,所以第一行的虚拟节点应该全部初始化为0,而左右两列不能初始化为0,因为为0的话就可能会参与最小值的计算,会影响到最终结果,所以应该初始化为正无穷大
本题的下标映射关系:因为本题给了一个矩阵,而我们又额外的加上一行和两列的虚拟节点,所以我们的下标都统一往右下角移动了一位,如果想找回之前对应的位置,那么下标需要进行统一减1(横纵坐标)
4. 填表顺序
本题的填表顺序是:从上往下填写每一行,每一行的值是从左往右
5. 返回值 :题目要求 + 状态表示
本题的返回值是:最后一行里面的最小值
3.代码
动态规划的固定四步骤:1. 创建一个dp表
2. 在填表之前初始化
3. 填表(填表方法:状态转移方程)
4. 确定返回值
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//本题是方形,所以不需要mint n = matrix.size();//多加了一行两列,初始化先把虚拟节点都初始化为正无穷大vector<vector<int>>dp(n + 1, vector<int>(n + 2, INT_MAX));//将虚拟节点的第一行初始化为0for (int j = 0; j < n + 2; j++) dp[0][j] = 0;//额外的加上一行和两列的虚拟节点,所以从1开始for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)//这里的matrix[i-1][j-1]也是加上一行和一列的虚拟节点,所以要横纵-1dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1]))+ matrix[i - 1][j - 1];//返回最后一行里面的最小值//定义一个临时变量ret,不能将ret的的值定义为0,不然会影响到最终结果int ret = INT_MAX;for (int j = 1; j <= n; j++)ret = min(ret, dp[n][j]);//找到最后一行的最小和return ret;}
};完结撒花~
相关文章:

动态规划 —— 路径问题-下降路径最小和
1. 下降路径最小和 题目链接: 931. 下降路径最小和 - 力扣(LeetCode)https://leetcode.cn/problems/minimum-falling-path-sum/description/ 2. 算法原理 状态表示:以莫一个位置位置为结尾 dp[i,j]表示:到…...

【Linux网络】TCP_Socket
目录 TCP协议(传输控制协议) listen状态 accept和connect TCP_echo_server (1)创建套接字 (2)绑定 (3)设置listen状态 (4)loop (5)客户端 多线程远程…...

NVR批量管理软件/平台EasyNVR多个NVR同时管理支持视频投放在电视墙上
在当今智能化、数字化的时代,视频监控已经成为各行各业不可或缺的一部分,无论是公共安全、交通管理、企业监控还是智慧城市建设,都离不开高效、稳定的视频监控系统的支持。而在这些应用场景中,将监控视频实时投放到大屏幕电视墙上…...
Springboot集成阿里云通义千问(灵积模型)
我这里集成后,做成了一个工具jar包,如果有不同方式的,欢迎大家讨论,共同进步。 集成限制: 1、灵积模型有QPM(QPS)限制,每个模型不一样,需要根据每个模型适配 集成开发思路: 因有…...

微信公众号(或微信浏览器)获取openId(网页授权)
下单支付需要openId 首先授权去拿到code --然后调用后太换取openId 1.去拿取code 下图中执行到window.location.href ( redirect_uri 传入当前路径-)–执行后重新跳转到当前页面–但是路径上会带上code参数 //然后调用后台方法–将code传给后台得到 o…...

C++算法第五天
本篇文章继续和大家一起刷算法题 第一题 题目链接 . - 力扣(LeetCode) 题目解析 题目要求: 这是一个连续的子数组 计算子数组内元素的和,若数组内元素的和符合 > target的值并且该子数组的长度是最短的,则返回…...

牛客网剑指Offer-树篇-JZ26 树的子结构
题目 来源:JZ26 树的子结构 描述 输入两棵二叉树A,B,判断B是不是A的子结构。(我们约定空树不是任意一个树的子结构) 假如给定A为{8,8,7,9,2,#,#,#,#,4,7},B为{8,9,2},2个树的结构如下ÿ…...

FFmpeg 4.3 音视频-多路H265监控录放C++开发六,使用SDLVSQT显示yuv文件
使用QT 显示YUV 文件 在最后一帧的时候会不停的显示最后一帧图片。 Vsqtshowyuv.h #pragma once#include <QtWidgets/QWidget> #include "ui_vsqtshowyuv.h" #include <sdl/SDL.h> #include <iostream> #include <fstream> #include <Q…...

Spring 设计模式之适配器模式
Spring 设计模式之适配器模式 适配器模式用到的场景java举例 适配器模式 适配器模式(Adapter Pattern)是一种结构型设计模式,它允许接口不兼容的类一起工作。 其核心思想是通过一个适配器类将不兼容的接口转换成客户端期望的另一个接口&…...

多传感器数字化分析系统
在工业飞速发展的今天,设备的安全稳定运行成为企业高效生产的关键因素。然而,传统的人工巡检方式面临着诸多挑战,如效率低下、漏检误检以及难以精准掌握设备运行状态等。旗晟凭借深厚的技术积累和创新精神,推出了多传感器数字化分…...

Java 基础教学:面向对象编程基础-封装、继承与多态
面向对象编程(OOP)是现代编程的重要范式,Java 语言提供了丰富的 OOP 特性,主要包括封装、继承和多态。本文将详细讲解这三个概念及其实现方式,并提供相应的代码示例。 1. 封装 1.1 概念 封装是将对象的状态…...
Ubuntu环境本地部署DbGate数据库管理工具并实现无公网IP远程访问
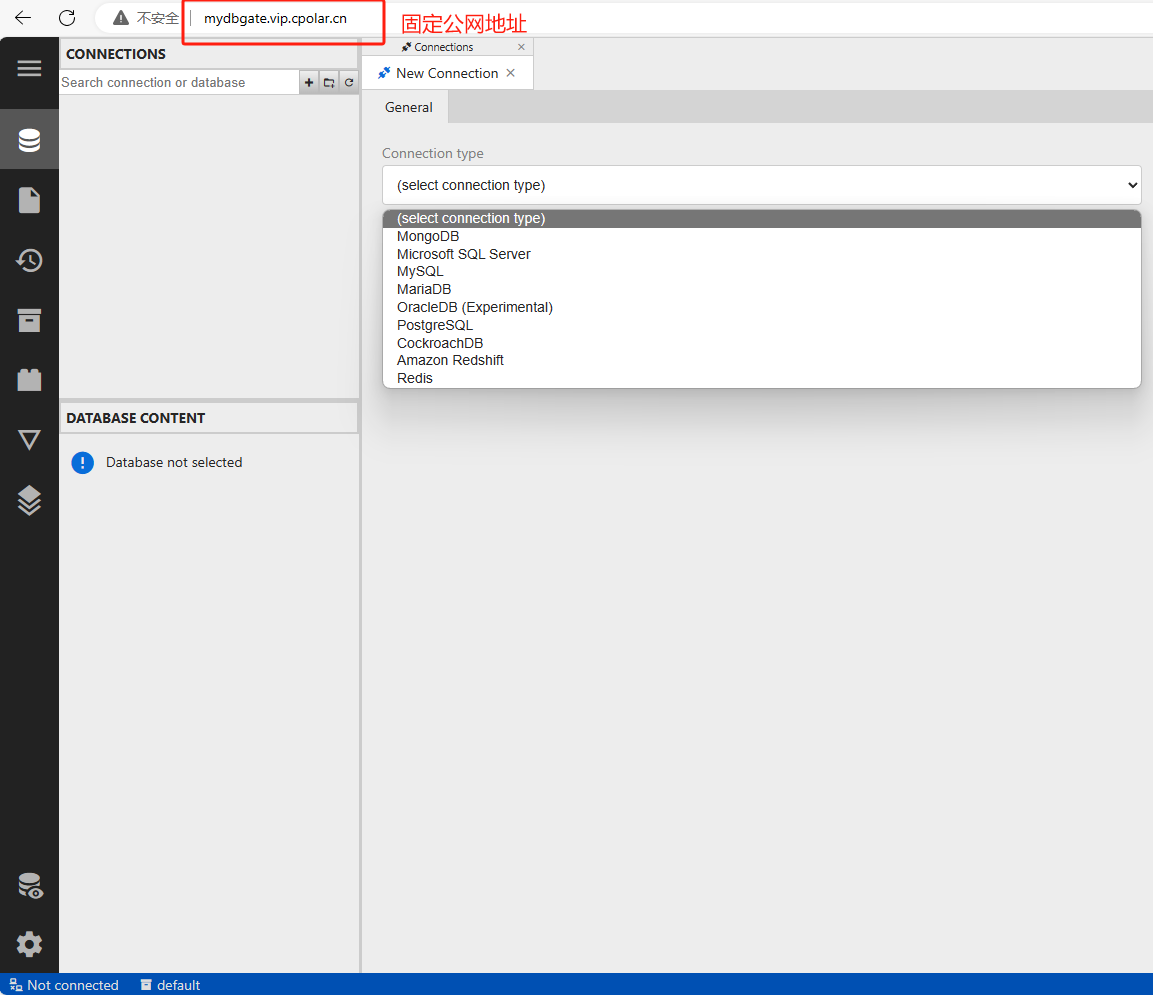
文章目录 前言1. 安装Docker2. 使用Docker拉取DbGate镜像3. 创建并启动DbGate容器4. 本地连接测试5. 公网远程访问本地DbGate容器5.1 内网穿透工具安装5.2 创建远程连接公网地址5.3 使用固定公网地址远程访问 前言 本文主要介绍如何在Linux Ubuntu系统中使用Docker部署DbGate数…...

【AI抠图整合包及教程】Meta SAM 2:视觉分割的革命性飞跃
在人工智能的浪潮中,每一次技术的革新都如同一场视觉盛宴,让我们见证着数字时代的变迁。Meta再次以Segment Anything Model 2(SAM 2)引领了图像和视频分割技术的新纪元。作为首个用于实时、可提示的图像和视频对象分割的统一模型&…...

使用语言模型进行文本摘要的五个级别(llm)
视频链接:5 Levels Of LLM Summarizing: Novice to Expert...

ubuntu交叉编译libffi库给arm平台使用
1.下载并解压: 2.生成makefile 编译: make 编译成功: 安装: make install 安装成功 查看安装后的libffi库...

【jvm】空间分配担保策略
目录 1. 说明2. 工作原理2.1 估算新生代存活对象大小2.2 判断老年代的剩余空间2.3 触发Full GC的条件 3. 相关参数与配置3.1 -XX:HandlePromotionFailure3.2 -XX:PretenureSizeThreshold3.3 -XX:MaxTenuringThreshold3.4 -XX:TargetSurvivorRatio 4.作用与意义 1. 说明 1.在Ja…...

iQOO手机怎样将屏幕投射到MacBook?可以同步音频吗?
众所周知,苹果品牌的设备自己有AirPlay的投屏功能,iPhone要投屏到MacBook只要连接同一网络,然后开启AirPlay就可以投屏。但其他品牌的手机没有AirPlay,怎么将手机屏幕投射到MacBook呢? 安卓系统的手机可以使用无线投屏…...

BUU usualCrypt1
查壳,32bit,丢进ida32中进行反编译,简单的不多说,直接进main分析 简单分析,打上注释,没啥好看的,就一个加密函数,加密完后和一个字符串进行比较,由此可以逆推出加密前的字…...

第十七章 标准库特殊设施
17.1 tuple类型 当希望将一些数据合成单一对象,但又不想麻烦地定义一个新数据结构来表示这些数据时,tuple非常有用。tuple是类似pair的模板。 tuple<size_t, size_t, size_t> threeD; //三个成员都设置为0//为每个成员提供初始值 tuple<strin…...

【格言分享】程序员的经典名言解读
上一期文章我们分享了一些程序员的经典名言,每一句都蕴含着深刻的道理。 接下来就给大家一个一个分析一下 这些格言确实捕捉到了编程和软件开发的精髓,每一条都蕴含着丰富的经验和智慧。下面我将逐一解释这些格言,并分享一些我的看法。 C程序员永远不会灭亡。他们只是cast…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...

关于 ffmpeg设置摄像头报错“Could not set video options” 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/148515355 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

HarmonyOS-ArkUI 自定义弹窗
自定义弹窗 自定义弹窗是界面开发中最为常用的一种弹窗写法。在自定义弹窗中, 布局样式完全由您决定,非常灵活。通常会被封装成工具类,以使得APP中所有弹窗具备相同的设计风格。 自定义弹窗具备的能力有 打开弹窗自定义布局,以…...

安装最新elasticsearch-8.18.2
1.环境我的环境是linux麒麟服务器 (安装 es 7.8以上 java环境必须11以上,可以单独配置es的java目录) 2.下载 官网的地址:下载 Elastic 产品 | Elastic Download Elasticsearch | Elastic Elasticsearch 入门 | Elasticsearch 中文文档 文档 3.我下载的是8.18的 Elasti…...

matlab模糊控制实现路径规划
路径规划是机器人和自动驾驶系统中的重要问题之一,它涉及确定如何在给定环境中找到最优路径以达到特定目标。模糊控制是一种有效的控制方法,可以应用于路径规划问题。 路径规划算法的目标是在避免障碍物的情况下,找到机器人或车辆从起点到终…...

