力扣11.1
2518. 好分区的数目
给你一个正整数数组 nums 和一个整数 k 。
分区 的定义是:将数组划分成两个有序的 组 ,并满足每个元素 恰好 存在于 某一个 组中。如果分区中每个组的元素和都大于等于 k ,则认为分区是一个好分区。
返回 不同 的好分区的数目。由于答案可能很大,请返回对 109 + 7 取余 后的结果。
如果在两个分区中,存在某个元素 nums[i] 被分在不同的组中,则认为这两个分区不同。
数据范围
1 <= nums.length, k <= 10001 <= nums[i] <= 109
分析
逆向思维,由于元素和大于等于 k k k的个数不是很好算,因此我们计算元素和小于 k k k的个数,由于每个数都必须被选择,因此实际我们考虑第一个集合的方案个数即可,这样就可以转化为01背包问题,我们令 d p [ i ] [ j ] dp[i][j] dp[i][j]为前 i i i个数,总和为 j j j的个数,对于第 i i i个数,有两种决策
- 选第 i i i个数: d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − n u m s [ i ] ] dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]] dp[i][j]=dp[i−1][j]+dp[i−1][j−nums[i]]
- 不选第 i i i个数: d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j]=dp[i-1][j] dp[i][j]=dp[i−1][j]
对于不选第 i i i个数,实际就是将他放到第二个集合
最后不合法的方案个数为 e r r = ∑ i = 0 k − 1 d p [ n ] [ i ] err=\sum_{i=0}^{k-1}dp[n][i] err=∑i=0k−1dp[n][i](其中n为nums的个数),因为集合一和二若互换元素也算一种方案,最后不合法方案 e r r ∗ 2 err*2 err∗2
**注意:**若 ∑ i = 0 n − 1 n u m s [ i ] < 2 ∗ k \sum_{i=0}^{n-1}nums[i]<2*k ∑i=0n−1nums[i]<2∗k,此时需要进行特判,因为在计算不合法数组方案的时候最后 e r r ∗ 2 err*2 err∗2会重复计算
考虑这样的例子, k = 10 , n u m s [ ] = 1 , 2 , 3 , 4 k=10,nums[]={1,2,3,4} k=10,nums[]=1,2,3,4
此时若第一个集合方案有{1}{2}{3}{4}{1,2}{1,3}{1,4}{2,3}{2,4}{3,4}{1,2,3}{1,2,4}{1,3,4}{2,3,4}{1,2,3,4},对于集合1为{1}的情况,集合2为{2,3,4},但是{2,3,4}也在集合1的方案中,因此实际此时已经包含了集合1:{1}集合2:{2,3,4},和集合1:{2,3,4},集合2:{1}的情况,但是最后err仍然乘了2,所以多算了一倍
代码
typedef long long LL;
class Solution {
public:const static LL N = 1005, mod = 1e9 + 7;LL dp[N][N];LL qpow(LL a, LL n) {LL res = 1;while(n) {if(n & 1) res = res * a % mod;a = a % mod * a % mod;n >>= 1;}return res;}int countPartitions(vector<int>& nums, int k) {int n = nums.size();LL tres = 0;for(auto tk : nums) {tres += tk;}if(tres < 2 * k) return 0;dp[0][0] = 1;for(int i = 0; i < n; i ++ ) {for(int j = 0; j < k; j ++ ) {dp[i + 1][j] = dp[i][j];if(j >= nums[i]) dp[i + 1][j] += dp[i][j - nums[i]];dp[i + 1][j] %= mod;}}LL t = 0;for(int i = 0; i < k; i ++ ) {t += dp[n][i];t %= mod;}t *= 2;LL res = ((qpow(2, n) - t + mod) % mod + mod) % mod; return res;}
};
3259. 超级饮料的最大强化能量
来自未来的体育科学家给你两个整数数组 energyDrinkA 和 energyDrinkB,数组长度都等于 n。这两个数组分别代表 A、B 两种不同能量饮料每小时所能提供的强化能量。
你需要每小时饮用一种能量饮料来 最大化 你的总强化能量。然而,如果从一种能量饮料切换到另一种,你需要等待一小时来梳理身体的能量体系(在那个小时里你将不会获得任何强化能量)。
返回在接下来的 n 小时内你能获得的 最大 总强化能量。
注意 你可以选择从饮用任意一种能量饮料开始。
数据范围
n == energyDrinkA.length == energyDrinkB.length3 <= n <= 1051 <= energyDrinkA[i], energyDrinkB[i] <= 105
分析
类似于打家劫舍,令dp[i][0]表示第i个数选择A数组的最大能量和,dp[i][1]表示第i个数选择B数组的最大能量和,状态转移如下:
- d p [ i ] [ 0 ] = m a x ( d p [ i − 2 ] [ 1 ] , d p [ i − 1 ] [ 0 ] ) + A [ i ] dp[i][0]=max(dp[i-2][1],dp[i-1][0])+A[i] dp[i][0]=max(dp[i−2][1],dp[i−1][0])+A[i]
- d p [ i ] [ 1 ] = m a x ( d p [ i − 2 ] [ 0 ] , d p [ i − 1 ] [ 1 ] ) + B [ i ] dp[i][1]=max(dp[i-2][0],dp[i-1][1])+B[i] dp[i][1]=max(dp[i−2][0],dp[i−1][1])+B[i]
考虑先选A和先选B两种情况
代码
typedef long long LL;
class Solution {
public:const static int N = 1e5 + 5;LL dp[N][2];LL maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {int n = energyDrinkA.size();dp[1][0] = energyDrinkA[0];for(int i = 1; i < n; i ++ ) {dp[i + 1][1] = max(dp[i - 1][0], dp[i][1]) + energyDrinkB[i];dp[i + 1][0] = max(dp[i][0], dp[i - 1][1]) + energyDrinkA[i];}LL res = max(dp[n][0], dp[n][1]);cout << dp[n][0] << " " << dp[n][1] << endl;memset(dp, 0, sizeof(dp));dp[1][1] = energyDrinkB[0];for(int i = 1; i < n; i ++ ) {dp[i + 1][0] = max(dp[i - 1][1], dp[i][0]) + energyDrinkA[i];dp[i + 1][1] = max(dp[i][1], dp[i - 1][0]) + energyDrinkB[i];}res = max(res, dp[n][0]);res = max(res, dp[n][1]);return res;}
};
相关文章:

力扣11.1
2518. 好分区的数目 给你一个正整数数组 nums 和一个整数 k 。 分区 的定义是:将数组划分成两个有序的 组 ,并满足每个元素 恰好 存在于 某一个 组中。如果分区中每个组的元素和都大于等于 k ,则认为分区是一个好分区。 返回 不同 的好分区…...

打印室预约系统|基于java和小程序的打印室预约系统设计与实现(源码+数据库+文档)
打印室预约系统 目录 基于java和小程序的打印室预约系统设计与实现 一、前言 二、系统设计 三、系统功能设计 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: 博主介绍:✌️大厂码农|毕设布道师&#x…...

操作系统-多线程案例
一、单例模式(是一种设计模式) 设计模式有很多种,不同的语法中也有不同的设计模式 单例 单个实例(对象) 某个类,在一个进程中,只应该创建出一个实例,(原则上不该有多个ÿ…...
什么是FUSE用户态文件系统
零. 文件系统 1. 为什么要有文件系统 文件系统是操作系统中管理文件和目录的一种机制。它提供了组织、存储、检索和更新文件的方法,主要如下: 数据组织:文件系统将数据组织成文件和目录,使用户能够更方便地管理和查找文件。每个…...
)
[每日一练]销售分析(通过数据的0/1转换进行是否存在的查询)
#该题目来源于力扣: 1083. 销售分析 II - 力扣(LeetCode) 题目要求: 表:Product----------------------- | Column Name | Type | ----------------------- | product_id | int | | product_name | varch…...

.NET Core WebApi第7讲:项目的发布与部署
一、理解 前端跟后端拿数据,然后在前端页面中展示,就是我们要完成的事情。 把前端跟后端开发好之后,我们需要落地部署,这个时候就需要一个服务器。 服务器就是一台电脑,只要windows里面有一个叫IIS的管理器。 二、项目…...

【python 将数据写入csv文件】正确方式
data [{username: jack, password: 1234}, ……]# 保存为CSV文件 with open(IP_output.csv, w, newline, encodingutf-8) as file:fieldnames [username, password]writer csv.DictWriter(file, fieldnamesfieldnames, quotingcsv.QUOTE_NONE)writer.writeheader() # 写入列…...

OpenCV4.8 开发实战系列专栏之 10 - 像素值统计
大家好,欢迎大家学习OpenCV4.8 开发实战专栏,长期更新,不断分享源码。 专栏代码全部基于C++ 与Python双语演示,专栏答疑群 请联系微信 OpenCVXueTang_Asst 本文关键知识点:像素值统计 最小(min)最大(max)均值(mean)标准方差(standard deviation)API知识点 最大最小值min…...

pandas计算相关性并画热力图
实现这个功能有很多方法,但是下面的方法还是比较优雅的: cols ["ASSET", "HOUSES", "INCOME", "DEBT", "EDUC"] corr df[cols].corr() corr.style.background_gradient(axisNone)讲解: …...
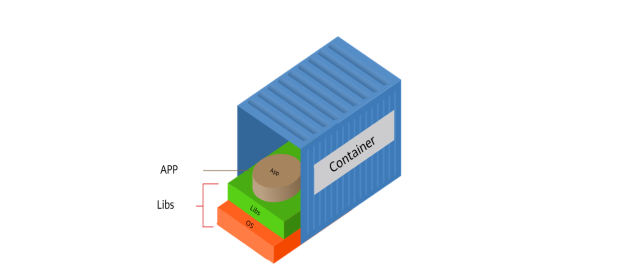
初始Docker
概述: 容器,作为云原生技术的重要组成部分,与虚拟机一样,均属于虚拟化技术的范畴。然而,容器技术以其独特的优势,在虚拟化领域中脱颖而出。与虚拟机不同,容器能够摆脱操作系统的束缚࿰…...

Redis-概念、安装、基本配置
文章目录 一、Redis及Redis集群概念、分布式系统概念一-1 Redis是什么一-2 什么是分布式系统、分布式缓存一-3 什么是Redis集群、实现Redis集群的方法有哪些、这些跟Redis的sentinel和cluster有什么关系一-4 Redis的库一-5 Redis中的Key与Value是什么、如何进行操作使用它们添加…...

qt QPlainTextEdit详解
QPlainTextEdit是一个功能强大、易于使用的纯文本编辑器/查看器。它使用与QTextEdit相同的技术和概念,但是为纯文本的处理进行了优化,因此更适合处理大型纯文本文档。QPlainTextEdit不提供富文本编辑功能,如字体、颜色、大小等的格式化&#…...

【机器学习】23. 聚类-GMM: Gaussian Mixture Model
1. 定义和假设 定义:probabilistic clustering(model-base) 假设:数据服从正态分布 2. 算法内容 我们假设数据是由k个高斯(正态)分布混合生成的。每个分布有2个参数:μ和σ。 一个分布对应一…...

深度探索C++对象模型
文章目录 前言一、关于对象C对象模型 二、构造函数实例分析 拷贝构造函数程序转化语意学(Program Transformation Semantics)成员初始化列表 三、数据语义学(The Semantics of Data)数据存取多种继承情况讨论仅单一继承加上虚函数多重继承虚拟继承 Pointer to Data Members 四、…...
电脑怎么设置开机密码:保障个人信息安全的第一步
在数字化时代,个人信息的安全至关重要。电脑作为我们日常工作和生活中不可或缺的设备,存储了大量的私人数据和敏感信息。为了防止未经授权的访问,设置开机密码是保护个人隐私和信息安全的基本措施之一。本文将详细介绍如何在不同操作系统下为…...

MybatisPlus入门(六)MybatisPlus-null值处理
一、MybatisPlus-null值处理 1.1)问题引入: 在查询中遇到如下情况,有部分筛选条件没有值,如商品价格有最大值和最小值,商品价格部分时候没有值。 1.2)解决办法: 步骤一:新建查询实…...

红帽认证有必要考吗?这四大人群推荐考取!
红帽认证(Red Hat Certification)作为全球公认的Linux技能认证,对于某些特定人群来说,考取这一认证无疑是一个明智的选择。本文将探讨红帽认证的必要性,并为四类人群提供考取红帽认证的建议。 1. IT专业人士 对于IT专业人士来说࿰…...
基于SSM+微信小程序的社团登录管理系统(社团1)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1 、功能描述 2、项目技术 3、开发环境 4、功能介绍 1、项目介绍 基于SSM微信小程序的社团登录管理系统实现了管理员及社团、用户。 1、管理员实现了首页、用户管理、社团管理、社团信息管理、社…...

html中cookie如何存储
在HTML中,可以使用JavaScript来创建、读取和删除cookie。以下是创建和读取cookie的基本示例: 创建cookie: function setCookie(name, value, daysToLive) { var cookie name "" encodeURIComponent(value); if (typeof daysToLive …...

C++基础三(构造函数,形参默认值,函数重载,单例模式,析构函数,内联函数,拷贝构造函数)
C有六个默认函数,分别是: 1、默认构造函数; 2、默认拷贝构造函数; 3、默认析构函数; 4、赋值运算符; 5、取址运算符; 6、取址运算符const; 构造函数 构造函数(初始化类成员变量): 1、属于类的成员函数之一 …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
