【笔面试常见题:三门问题】用条件概率、全概率和贝叶斯推导
1. 问题介绍
三门问题,又叫蒙提霍尔问题(Monty Hall problem),以下是蒙提霍尔问题的一个著名的叙述,来自Craig F. Whitaker于1990年寄给《展示杂志》(Parade Magazine)玛丽莲·沃斯·莎凡特(Marilyn vos Savant)专栏的信件:
假设你正在参加一个游戏节目,你被要求在三扇门中选择一扇:其中一扇后面有一辆车;其余两扇后面则是山羊。你选择了一道门,假设是一号门,然后知道门后面有什么的主持人,开启了另一扇后面有山羊的门,假设是三号门。他然后问你:“你想选择二号门吗?”变换你的选择对你来说是一种优势吗?

2. 事件定义
不失一般性,假设我们最初选择1号门,然后主持人打开3号门。定义事件如下:
- A 1 = A_1= A1= 汽车在1号门后
- A 2 = A_2= A2= 汽车在2号门后
- A 3 = A_3= A3= 汽车在3号门后
- B 3 = B_3= B3= 主持人打开3号门
根据题意不难得到:
- P ( A 1 ) = P ( A 2 ) = P ( A 3 ) = 1 3 P(A_1)=P(A_2)=P(A_3)=\frac{1}{3} P(A1)=P(A2)=P(A3)=31
- 如果汽车在1号门后,那么主持人可以选择打开2号门或3号门。主持人打开3号门的概率是二分之一,此时: P ( B 3 ∣ A 1 ) = 1 2 P(B_3|A_1)=\frac{1}{2} P(B3∣A1)=21
- 如果汽车在2号门后,主持人只能打开3号门(因为门1是你选的,门2有汽车),此时: P ( B 3 ∣ A 2 ) = 1 P(B_3|A_2)=1 P(B3∣A2)=1
- 如果汽车在3号门后,主持人不会打开3号门,此时: P ( B 3 ∣ A 3 ) = 0 P(B_3|A_3)=0 P(B3∣A3)=0
计算概率
如果我们选择换门,则赢得汽车的概率就等于主持人打开3号门后,汽车在2号门的概率,即: P ( A 2 ∣ B 3 ) P(A_2|B_3) P(A2∣B3)。
根据贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
P ( A 2 ∣ B 3 ) = P ( B 3 ∣ A 2 ) P ( A 2 ) P ( B 3 ) = P ( B 3 ∣ A 2 ) P ( A 2 ) ∑ i = 1 3 P ( B 3 ∣ A i ) P ( A i ) = 1 / 3 1 / 2 = 2 3 \begin{align} P(A_2|B_3)=&\frac{P(B_3|A_2)P(A_2)}{P(B_3)}\notag\\ =&\frac{P(B_3|A_2)P(A_2)}{\sum_{i=1}^3P(B_3|A_i)P(A_i)}\notag\\ =&\frac{1/3}{1/2}\notag\\ =&\frac{2}{3}\notag \end{align} P(A2∣B3)====P(B3)P(B3∣A2)P(A2)∑i=13P(B3∣Ai)P(Ai)P(B3∣A2)P(A2)1/21/332
相似的,如果我们选择不换门,则赢得汽车的概率就等于主持人打开3号门后,汽车还在1号门后的概率: P ( B 3 ∣ A 1 ) = P ( B 3 ∣ A 1 ) P ( A 1 ) P ( B 3 ) = 1 3 P(B_3|A_1)=\frac{P(B_3|A_1)P(A_1)}{P(B_3)}=\frac{1}{3} P(B3∣A1)=P(B3)P(B3∣A1)P(A1)=31
总结,选择换门,赢得汽车的概率是2/3,选择不换,赢得汽车的概率是1/3,所以果断换门。
相关文章:

【笔面试常见题:三门问题】用条件概率、全概率和贝叶斯推导
1. 问题介绍 三门问题,又叫蒙提霍尔问题(Monty Hall problem),以下是蒙提霍尔问题的一个著名的叙述,来自Craig F. Whitaker于1990年寄给《展示杂志》(Parade Magazine)玛丽莲沃斯莎凡特&#x…...

刘艳兵-DBA011-应用使用Oracle数据库,必须启动哪些服务?
应用使用Oracle数据库,必须启动哪些服务( ) A OracleServiceSID B OracleJobSchedulerSID C OracleMTSRecoveryService D OracleHOME_NAMETNSListener 答: A OracleServiceSID D OracleHOME_NAMETNSListener…...

注释多行代码的vim插件
编写vim 插件代码 add_comments.vim function! AddComment()let l:comment #if &filetype cpplet l:comment //elseif &filetype clet l:comment //endiflet [l:start, l:end][ line("<"), line(">") ]let l:commented_lines []for …...

Docker 安装HomeAssistant智能家居系统
HomeAssistant 介绍 简介 Home Assistant是一个自由开源的智能家居自动化平台,它可以控制并监测各种智能家居设备、传感器和其他物联网设备。Home Assistant可以运行在树莓派、NVIDIA Jetson Nano等低功耗设备上,使用户可以快速搭建自己的智能家居系统。…...

21 Docker容器集群网络架构:四、Docker集群网络验证
文章目录 Docker容器集群网络架构:四、Docker集群网络验证4.1 创建网络4.2 查看创建的网络4.2.1 查看节点1创建的网络4.2.2 查看节点2创建的网络4.2.3 查看节点3创建的网络4.3 运行容器并查看4.3.1 运行容器4.3.2 节点1查看4.3.3 节点2查看4.3.4 节点3查看Docker容器集群网络架…...

【Kaggle | Pandas】练习5:数据类型和缺失值
文章目录 1. 获取列数据类型.dtype / .dypes2. 转换数据类型.astype()3. 获取数据为空的列 .isnull()4. 将缺少值替换并且排序.fillna(),.sort_values() 1. 获取列数据类型.dtype / .dypes 数据集中points列的数据类型是什么? # Your code here dtype …...

《YOLO 目标检测》—— YOLO v4 详细介绍
文章目录 一、整体网络结构1. YOLO v4 网络结构图2.对之前版本改进创新的概括 二、对改进创新部分的具体介绍1. 输入端创新2. Backbone主干网络创新CSPDarknet53Mish激活函数Dropblock正则化 3. 特征融合创新SPP模块PAN结构 4. Prediction输出层创新(未写完…...

Ubuntu:通过ssh链接另外一台Ubuntu
本文将介绍通过ssh链接另外一台Ubuntu的方法。 一、安装openssh-server sudo apt update sudo apt install openssh-server二、查看SSH是否运行 sudo systemctl status ssh三、链接 ssh usernameremote_ip_address四、复制A电脑的文件到本地 scp usernameremote_ip_addres…...

黄山谷捷提交创业板IPO注册,募资扩产提升综合竞争力
近日,黄山谷捷股份有限公司(下文称“黄山谷捷”)申请深交所创业板IPO审核状态变更为“提交注册”。据悉,本次IPO黄山谷捷拟募资50,201.19万元,分别用于功率半导体模块散热基板智能制造及产能提升项目,研发中…...
如何进行加密)
(python)如何进行加密
代码效果是将输入的四个数字每个加上7,然后除以10的余数,接着再将第一个数字和第三个数字对调,第二个数字和第四个数字对调 # 获取用户输入的四位数字符串 list1 input("请输入你四位数密码:") # 初始化一个空列表来存…...
夸克网盘免费扩容 20T 福利,无限次叠加,亲测有效
新用户用夸克 APP 存资源可得 1T 永久存储空间 🚨此方法仅试用于新用户,并且只能在手机上打开夸克 APP 中去领取!pc,ipad 都不行!!! 使用手机打开夸克 APP,保存以下资源可获取 1T …...
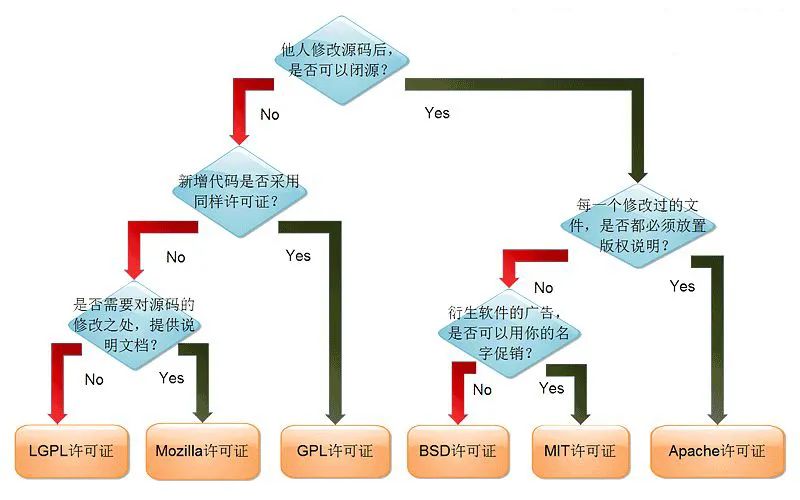
开源协议类型及长安链开源协议介绍
截至目前,我国参与国际开源社区协作的开发者数量排名全球第二并推出了众多社区活跃度较高的高质量开源项目,是全球开源生态的重要贡献力量,但在开源治理方面我国还处于发展初期,大部分开发者对开源的印象还限于开放代码、免费使用…...
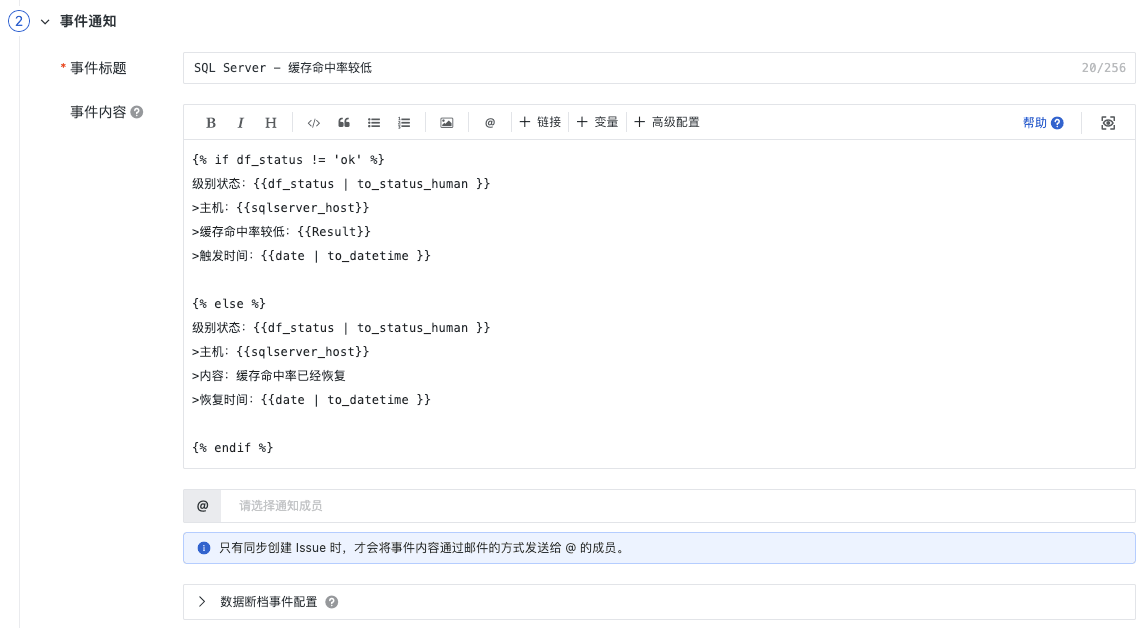
SQL Server 可观测最佳实践
SQL Server 简介 SQL Server 是微软公司开发的一款关系数据库管理系统,支持企业 IT 环境中的各种事务处理、商业智能和分析应用程序。它支持多种操作系统平台,而无论是物理还是虚拟形式,自建部署环境还是在云环境中,运行的操作系…...

青少年编程能力等级测评CPA Python编程(一级)
青少年编程能力等级测评CPA Python编程(一级) (考试时间90分钟,满分100分) 一、单项选择题(共20题,每题3.5分,共70分) 下列语句的输出结果是( )。 print(35*2) A&a…...

WebSocket 连接频繁断开的问题及解决方案
文章目录 WebSocket 连接频繁断开的问题及解决方案1. 引言2. 什么是 WebSocket?2.1 WebSocket 的优势2.2 WebSocket 的工作原理 3. WebSocket 连接频繁断开的常见原因3.1 服务器端问题3.1.1 服务器负载过高3.1.2 服务器配置不当3.1.3 超时设置 3.2 网络问题3.2.1 网…...

[CSP篇] CSP2024 游记(上)
Part.0 前言 在刚刚过去的 CSP-J2024 以及 CSP-S2024 中,不知大家十分用自己最好的状态参加了这次重要的测试,取得了令自己努力的成绩呢? 文章发布在 2024 年 11 月 1 日,距离出结果还有 3 − 5 3-5 3−5 天,如有需…...

Mac “屏幕保护程序启动或显示器关闭后需要密码“无效
屏幕保护程序启动或显示器关闭后需要密码只能选择“立即”的解决方法: 在 iPhone mirror中设置,每次询问权限。 参考:https://support.apple.com/en-us/120421...

架构师之路-学渣到学霸历程-35
Nginx的配置文件说明 nginx的学习,到了关键的部分,其实想要学好nginx就一定要了解配置文件;我们看看配置文件是怎么样的? 1、nginx的配置文件路径 不同的安装方式、nginx的配置文件路径也有所不同 源码安装配置文件路径&#…...

2024-10月的“冷饭热炒“--解读GUI Agent 之computer use?phone use?——多模态大语言模型的应用进阶之路
GUI Agent 之computer use?phone use?——多模态大语言模型的进阶之路 1.最新技术事件浅析三、思考和方案设计工具代码部分1.提示词2.工具类API定义,这里主要看computer tool就够了 总结 本文会总结概括这一应用的利弊,然后给出分析和工具代…...

sheng的学习笔记-AI基础-激活函数
ai目录:sheng的学习笔记-AI目录-CSDN博客 目录 Sigmoid Tanh 函数 ReLU(Rectified Linear Unit)函数 Leaky ReLU ELU(Exponential Linear Unit) SEIU Swish 激活函数的选择 激活函数(Activation F…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
