动态规划 - 编辑距离
115. 不同的子序列
困难
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 + 7 取模。

算法思想:利用动态规划,分s[i - 1] 与 t[j - 1]相等,s[i - 1] 与 t[j - 1] 不相等两种情况具体讨论如何匹配。
1、dp数组及其下标含义:dp[i][j] 以i-1为结尾的字符串s中包含以j-1为结尾的字符串t
的个数。
2、递推公式:
- s[i - 1] 与 t[j - 1]相等: dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
- s[i - 1] 与 t[j - 1] 不相等: dp[i][j] = dp[i - 1][j]
如果s[i-1] == t[j-1],dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配.
如果s[i-1] != t[i-1],那么不能用s[i-1]来匹配(模拟在s中删除这个元素),dp[i][j] = dp[i-1][j]
3、初始化
dp[0][0] = 1, dp[i][0] = 1(s匹配空字符串,删除到为空这一种方法),dp[0][j] = 0()
4、遍历
从前到后,从上到下
class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(len(s)):dp[i][0] = 1for j in range(1, len(t)):dp[0][j] = 0for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j] #用s[i - 1]来匹配和不用else:dp[i][j] = dp[i-1][j]# 不能用s[i-1]来匹配(模拟在s中删除这个元素)return dp[-1][-1]583. 两个字符串的删除操作
中等
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。

直接删
算法思想:利用动态规划,如果word1[i-1] == word2[j-1]相等,那么不需要删除操作,如果不相等,那么可以删word1、word2或者都删,取最小值。
1、dp数组及其下标含义:dp[i][j] 以i-1为结尾的字符串word1和以j-1为结尾的字符串word2
最少需要删除几次可以相等。
2、递推公式:
- s[i - 1] 与 t[j - 1]相等: dp[i][j] = dp[i - 1][j - 1]
- s[i - 1] 与 t[j - 1] 不相等: dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1,dp[i-1][j-1]+2)
如果s[i-1] == t[j-1],不需要删。dp[i][j] = dp[i - 1][j - 1]
如果s[i-1] != t[i-1],有三种删除方式,删word1/word2/都删,取最小值
3、初始化
dp[0][0] = 1, dp[i][0] = i;dp[0][j] = j
4、遍历
从前到后,从上到下
class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(1, len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1] # 相等的话,不需要删else: # 不相等,可以删word1\word2\都删 dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1,dp[i-1][j-1]+2)return dp[-1][-1]求最长公共子序列
class Solution(object):def minDistance(self, word1, word2):m, n = len(word1), len(word2)# dp 求解两字符串最长公共子序列dp = [[0] * (n+1) for _ in range(m+1)]for i in range(1, m+1):for j in range(1, n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])# 删去最长公共子序列以外元素return m + n - 2 * dp[-1][-1]72. 编辑距离
中等
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符

1、dp数组及其下标含义:dp[i][j] 以i-1为结尾的字符串word1和以j-1为结尾的字符串word2
最少需要操作几次可以相等。
2、递推公式:
- s[i - 1] 与 t[j - 1]相等: dp[i][j] = dp[i - 1][j - 1]
- s[i - 1] 与 t[j - 1] 不相等: dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1,dp[i-1][j-1]+1)
如果s[i-1] == t[j-1],不需要操作。dp[i][j] = dp[i - 1][j - 1]
如果s[i-1] != t[i-1],可以插入、删除、替换
- 删除:删word1: dp[i][j] = dp[i - 1][j] +1;删word2: dp[i][j] = dp[i][j-1] +1
- 插入:相当于删除
- 替换:只需一次操作,dp[i][j] = dp[i - 1][j - 1] + 1
3、初始化
dp[0][0] = 1, dp[i][0] = i;dp[0][j] = j
4、遍历
从前到后,从上到下
class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:# 相等无需操作dp[i][j] = dp[i-1][j-1]else: # 不相等,进行删除或替换操作,取最小值dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1return dp[-1][-1]
相关文章:

动态规划 - 编辑距离
115. 不同的子序列 困难 给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 7 取模。 算法思想:利用动态规划,分s[i - 1] 与 t[j - 1]相等,s[i - 1] 与 t[j - 1] 不相等两种情况具…...
力扣——113. 路径总和
113. 路径总和 II 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [5,4,8,11,null,13,4,7,2,null,null,5,1], t…...

C02S04-Ubuntu基本使用
一、Ubuntu初始配置 1. 使用root用户 Ubuntu系统默认只能使用普通用户,要想使用root用户,需要先设置root用户密码。 进入终端,配置root用户密码。按照提示输入密码。 sudo passwd root配置完成后,执行下面的密码,切换…...

C语言 | Leetcode C语言题解之第525题连续数组
题目: 题解: struct HashTable {int key, val;UT_hash_handle hh; };int findMaxLength(int* nums, int numsSize) {int maxLength 0;struct HashTable* hashTable NULL;struct HashTable* tmp malloc(sizeof(struct HashTable));tmp->key 0, tm…...

Qml-Transition的使用
Qml-Transition的使用 Transition的概述 Transition:定义了当状态发生改变时应用的动画属性animations : list:(Transition)过渡的动画属性enabled : bool:状态发生变化时,是否使能此过渡(Transition)动画…...

Notepad++检索包含多个关键字的行
Notepad检索包含多个关键字的行 在Notepad中,你可以使用正则表达式来检索包含多个关键字的行。以下是具体步骤: 打开Notepad,打开要搜索的文件。 点击菜单栏上的“搜索”选项,然后选择“查找”。 在弹出的查找对话框中…...

C语言:水仙花树,要求三位以上的N位整数每位的N次方等于数本身,全部输出出来
#include <stdio.h> int main() { int n; scanf("%d",&n);//这里是说明多少n位整数 int first1; int i1; while(i<n){//此while循环可以得到n位数的最小位,例如3位的100. first*10; i; } ifirst; whil…...
金融贷款口子超市V2源码 Thinkphp开发的贷款和超市平台源码(亲测源码含安装视频教程)
金融贷款口子超市V2源码 Thinkphp开发的贷款和超市平台源码 源码下载:https://download.csdn.net/download/m0_66047725/89938268 更多资源下载:关注我。...

redis的三种客户端
在 Redis 中,常用的 Java 客户端有三种:Jedis、Lettuce 和 Redisson。它们各有特点,适用于不同的场景。以下是它们的详细介绍,以及如何在 Spring Boot 中集成 Redis。 一、Redis 三种常用客户端详解 1.1 Jedis Jedis 是 Redis 官…...
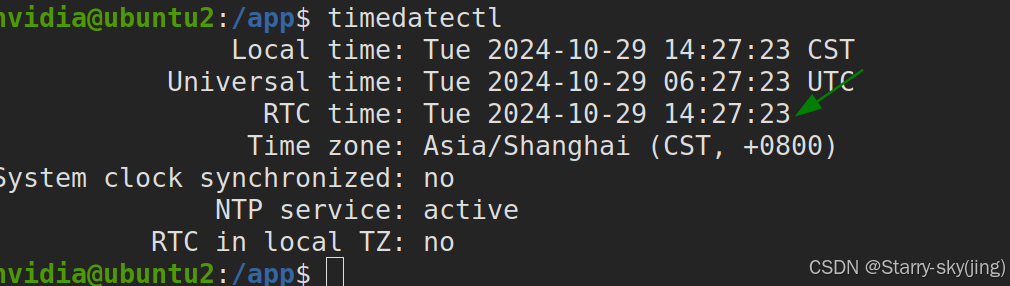
边缘计算【智能+安全检测】系列教程--agx orin解决RTC时间问题
因为是离线运行,首要问题是时间不准确,就在主板上加装了纽扣电池,但是会有一系列问题,比如无法将RTC时间回写到系统时间,或者无法将系统时间写到RTC中等等一些列问题。为解决这些问题,一劳永逸的方式&#…...

数据库动态扩容:Java实现与技术策略
引言 数据库动态扩容是应对数据量增长和业务需求变化的关键技术。它允许数据库系统在不停机的情况下,通过增加或减少资源来适应业务负载的变化。本文将详细介绍数据库动态扩容的工作原理、技术策略,并提供Java代码示例。 1. 数据库动态扩容的工作原理 …...

Golang | Leetcode Golang题解之第525题连续数组
题目: 题解: func findMaxLength(nums []int) (maxLength int) {mp : map[int]int{0: -1}counter : 0for i, num : range nums {if num 1 {counter} else {counter--}if prevIndex, has : mp[counter]; has {maxLength max(maxLength, i-prevIndex)} …...

低代码架构浅析
低代码的定义与应用场景 定义 低代码平台是一种通过可视化工具和预定义组件实现快速应用开发的环境,显著减少了编码量。它旨在简化开发流程,加快应用交付,提高开发效率,使非技术人员也能参与应用开发。 应用场景 企业内部应用 …...

mysql字段是datetime如何按照小时来统计
在 MySQL 中,如果你有一个包含 DATETIME 类型的列,并且你想按照小时来统计数据,可以使用 DATE_FORMAT 函数将 DATETIME 列格式化为仅包含日期和小时的形式,然后使用 GROUP BY 子句来分组。 假设你有一个名为 events 的表…...

nacos快速启动
预备环境准备: 确保是64 bit OS(推荐Linux/Unix/Mac),安装64 bit JDK 1.8并下载&配置,安装Maven 3.2.x并下载&配置。 下载源码或者安装包: 从Github上下载源码方式: git clone https://…...

@Excel若依导出异常/解决BusinessBaseEntity里面的字段不支持导出
今天发现所有实体类继承BusinessBaseEntity里面的这些通用字段不支持导出,debug时发现是这样: 导出效果 这里我把能查到的方法都汇总了,如果你也遇到这个异常,可以去逐步排查 1.先看库里有没有数据 2.看字段名是否对齐 3.所需要…...

虚拟机 Email 恢复专用工具:Virtual Machine Email Recovery
天津鸿萌科贸发展有限公司从事数据安全服务二十余年,致力于为各领域客户提供专业的数据恢复、数据备份解决方案与服务,并针对企业面临的数据安全风险,提供专业的相关数据安全培训。 天津鸿萌科贸发展有限公司是 SysTools 系列数据恢复、取证及…...

代理人工智能如何应对现代威胁的速度和数量
Seven AI首席执行官 Lior Div 讨论了代理 AI 的概念及其在网络安全中的应用。他解释了代理 AI 与传统自动化安全系统的区别,即代理 AI 具有更大的自主性和决策能力。 Div 强调,通过实时处理大量警报,代理 AI 特别适合对抗现代 AI 驱动的威胁…...

element-plus版本过老,自写选项弹框增删功能
title: element-plus版本过老,自写选项弹框增删功能 date: 2024-10-31 10:53:18 tags: element-plus 1.情景 发现代码怎么都用不了el-select的#footer插槽从而实现不了相关的操作,发现el-select自带的管理相关数据的属性popper-class用不了。 2.原因与…...

Python毕业设计选题:基于django+vue的宠物寄养平台的设计与实现
开发语言:Python框架:djangoPython版本:python3.7.7数据库:mysql 5.7数据库工具:Navicat11开发软件:PyCharm 系统展示 1. 前台系统功能模块 系统首页界面 用户注册界面 用户登录界面 宠物商城界面 宠物店…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
