动态规划应该如何学习？

动态规划如何学习

参考灵神的视频和题解做的笔记（灵神YYDS，以后也都会用这套逻辑去思考）

枚举选哪个：

动态规划入门：从记忆化搜索到递推_哔哩哔哩_bilibili

746. 使用最小花费爬楼梯 - 力扣（LeetCode）
选或不选：

0-1背包 完全背包_哔哩哔哩_bilibili
494. 目标和 - 力扣（LeetCode）

个人觉得枚举选哪个和选或不选的区别是
枚举选哪个是在回溯函数中有for循环
而选或不选只有两个选择，一般会是二叉树

学习步骤：

1.思考递归回溯的暴力穷举法（即深度优先遍历DFS）

注意要画树形结构，画完很容易看出哪里是重复的计算，对改成记忆化搜索有好处

可以使用代码随想录的递归三部曲

2.改成记忆化搜索，就是准备一个备忘录数组，保存已经计算过的结果

3.把记忆化搜索1:1翻译成为DP

翻译的时候可以想想代码随想录的动规五部曲，其实到这里五部曲的内容已经全部解决了

刷了几道题以后的发现：
1.思考回溯的时候一般就会把dp数组和下标的含义给想清楚，这一过程就是分割子问题的过程，不然回溯想不出来的

2.回溯算法终止条件一般是dp数组的初始化

3.记忆化搜索一般是自底向上，和动态规划的从前往后其实是一样的，只是记忆化是递归里的栈，而动态规划是for循环

4.dfs函数就是dp数组

5.dfs一般传入的参数n在动态规划里面一般是一层for循环，dfs中如果有for循环，那动态规划的递推一般是两层循环，而且n可以和循环中的一个进行替换

**动态规划有「选或不选」和「枚举选哪个」两种基本思考方式。**在做题时，可根据题目要求，选择适合题目的一种来思考。

枚举选哪个

746.使用最小花费爬楼梯

746. 使用最小花费爬楼梯 - 力扣（LeetCode）

第一步：回溯法（深度优先遍历）

这个过不了，时间复杂度太高，但是这是学习动态规划的必由之路

思路：

首先思考子问题并画出树形结构图

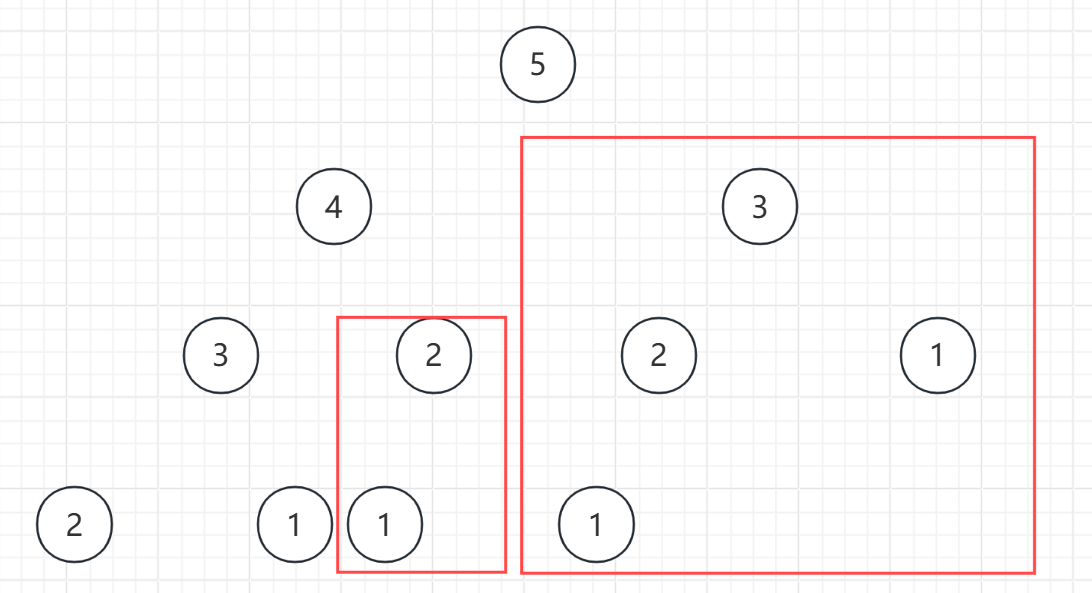
我们要求到第5个台阶的最小花费，我们可以从第4个加上4的花销上一个台阶，也可以从3加上3的花销上两个台阶

我们要求到第n个台阶的最小花费，我们可以从第n-1个加上n-1的花销上一个台阶，也可以从n-2加上n-2的花销上两个台阶，n-1就是下一个要求的子问题，由n-2和n-3得到，一直到1或2，它的花费就是0，因为可以选择从1或2开始爬楼梯

这样就得到了一个二叉树（以5为例子）

我们要到5的台阶，就要依靠到达4和到达3的结果，来比较得到最小值，所以要得到下层结点向上层返回的结果，那就得用后序遍历来得到4,3的结果

1.返回值和参数

我们要下层结点的最小值，所以要int

cost是题目中的花费数组，index是记录我们遍历到哪里了，相当于for循环里面的i

int dfs(vector<int>& cost,int index)

2.终止条件

if(index==0||index==1)return 0;

0其实是第一个台阶，1其实是第二个台阶，因为cost数组从0开始。

爬第一个或第二个台阶不需要花费，所以直接返回0

3.本层逻辑

左子树返回爬上第n-1台阶的最小值

右子树返回爬上第n-2台阶的最小值

最后本层返回的就是两者的最小值作为结果

int l=dfs(cost,index-1)+cost[index-1];
int r=dfs(cost,index-2)+cost[index-2];
return min(l,r);

完整代码：

class Solution {
public:int dfs(vector<int>& cost,int index){if(index==0||index==1)return 0;int l=dfs(cost,index-1)+cost[index-1];int r=dfs(cost,index-2)+cost[index-2];return min(l,r);}int minCostClimbingStairs(vector<int>& cost) {return dfs(cost,cost.size());}
};

C++还可用lambda来写

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {function<int(int)> dfs=[&](int index)->int{if(index==0||index==1)return 0;return min(dfs(index-1)+cost[index-1],dfs(index-2)+cost[index-2]);};return dfs(cost.size());}
};

第二步：改成记忆化搜索

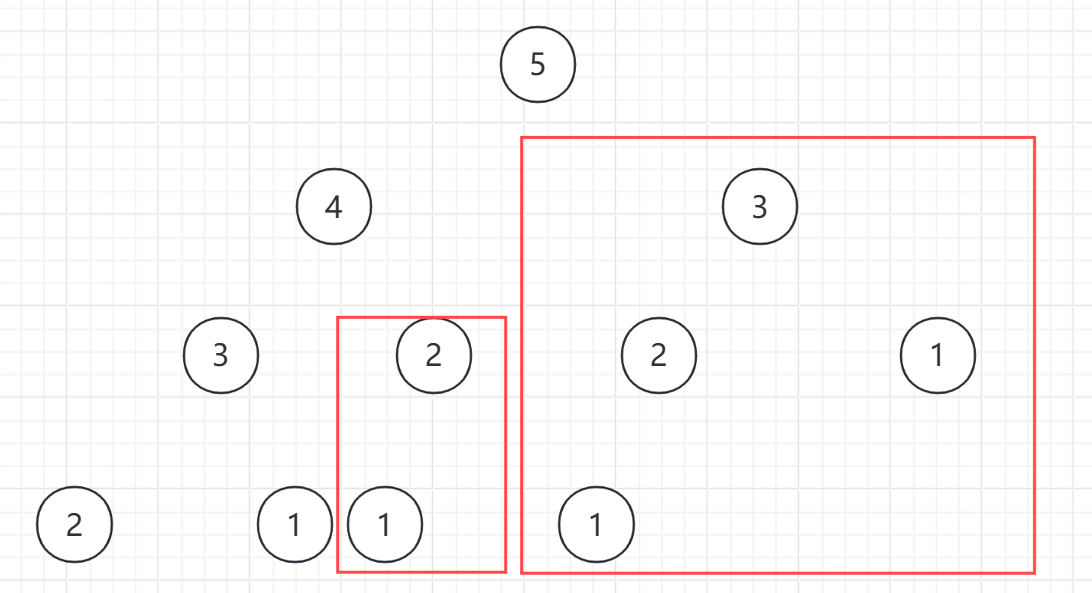
从图中可以看到，这些地方就是重复计算的地方，可以直接砍掉。

怎么砍呢？

我们在遍历过程中，如果是第一次碰到这个数字呢，我们就把它的计算结果给保存到一个数组当中去，下次要用的话直接从数组里面拿而不用再次进行递归计算了。

砍完之后还剩下啥：只需要计算3,4,5，你会发现时间复杂度竟然变成了O(n)，成了线性的，那这不就和递推一样了么？用1,2计算3，用2,3计算4，用3,4计算5得出结果。

在递归进行记忆化搜索里面，这是自底向上的计算，算5，要去递归3,4，然后一层一层递归

到最后1和2的时候直接返回0，然后得出3的最小，然后根据2,3得出4的最小，最后一层一层返回知道最后。

下面就来看递推。

完整代码：

class Solution {
public:int dfs(vector<int>& cost,vector<int>& dp,int index){if(index==0||index==1)return 0;//碰到了算过的，那就直接返回if(dp[index]!=-1)return dp[index];int l=dfs(cost,dp,index-1)+cost[index-1];int r=dfs(cost,dp,index-2)+cost[index-2];return dp[index]=min(l,r);//1.return dp[index]=min(dfs(cost,dp,index-1)+cost[index-1],dfs(cost,dp,index-2)+cost[index-2]);这样写也行//2.dp[index]=min(l,r);//return dp[index];也行}int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1,-1);return dfs(cost,dp,cost.size());}
};

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1,-1);function<int(int)> dfs=[&](int index)->int{if(index==0||index==1)return 0;if(dp[index]!=-1)return dp[index];int& res=dp[index];return res=min(dfs(index-1)+cost[index-1],dfs(index-2)+cost[index-2]);};return dfs(cost.size());}
};

注意点：
1.传入的dp备忘录必须是引用传入，不然的话下层的结果保存不到数组里面，每一层的dp数组还全都是-1，就和DFS逻辑一样了其实。dp数组不会起到任何作用

2.对dp[index]一定要赋值，不能直接返回min(l,r)，不然dp数组不会更新

3.l和r不可以替换成dp[index-1]和dp[index-2]。（如果有小伙伴不幸和一样犯了这个错误，那就继续看吧）

int dp[index-1]=dfs(cost,dp,index-1)+cost[index-1];
int dp[index-2]=dfs(cost,dp,index-2)+cost[index-2];
return dp[index]=min(l,r);

我先说答案：这种乍一看挺对的，实际上没有想清楚dfs返回值到底是什么，dfs（index-1）的返回值是dp[index-1]，如果再加上cost[index-1]，那得到的应该是dp[index]，而不是dp[index]。

下面是我没彻底弄懂之前写的，只是记录一下自己的思考过程，不想看的可以跳过了

这种方式会刷新我们已经保存过的dp[index]，就比如起始的0和1，dp[0]和dp[1]花费最小值本来都是0，但是用这个在计算dp[3]的时候会把dp[0]和dp[1]赋值为cost[0]和cost[1]。

然后dp[2]=dp[0]+cost[0]=2，可是我们一看这肯定是1怎么能是2呢？

后面的dp[3]也是最开始被更新为3，后面直接变成4了，这就是再次刷新了

输入
cost =
[1,100,1,1,1,100,1,1,100,1]
标准输出
index=2
1 100 -1 -1 -1 -1 -1 -1 -1 -1 -1 
index=3
1 100 2 -1 -1 -1 -1 -1 -1 -1 -1 
index=4
1 100 3 3 -1 -1 -1 -1 -1 -1 -1 
index=5
1 100 3 4 4 -1 -1 -1 -1 -1 -1 
index=6
1 100 3 4 5 104 -1 -1 -1 -1 -1 
index=7
1 100 3 4 5 204 6 -1 -1 -1 -1 
index=8
1 100 3 4 5 204 7 7 -1 -1 -1 
index=9
1 100 3 4 5 204 7 8 107 -1 -1 
index=10
1 100 3 4 5 204 7 8 207 9 -1 

正确的打印：

cost =
[1,100,1,1,1,100,1,1,100,1]
标准输出
index=2
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 
index=3
-1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 
index=4
-1 -1 1 2 -1 -1 -1 -1 -1 -1 -1 
index=5
-1 -1 1 2 2 -1 -1 -1 -1 -1 -1 
index=6
-1 -1 1 2 2 3 -1 -1 -1 -1 -1 
index=7
-1 -1 1 2 2 3 3 -1 -1 -1 -1 
index=8
-1 -1 1 2 2 3 3 4 -1 -1 -1 
index=9
-1 -1 1 2 2 3 3 4 4 -1 -1 
index=10
-1 -1 1 2 2 3 3 4 4 5 -1 

第三步：一比一翻译成动态规划(递推)

1.确定dp数组以及下标的含义

dp数组含义是登上第i个台阶由多少种方法

i下标就是第i+1个台阶

2.确定递推公式

dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);

这个就是在回溯的两个选择里面挑一个小的

就是记忆化搜索里面的返回值

3.dp数组如何初始化

就是回溯里面的终止条件

vector<int> dp(cost.size()+1,-1);
dp[0]=0,dp[1]=0;

4.确定遍历顺序

后面的5要依靠前面3,4的计算结果，所以肯定是正向遍历

完整代码：

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1,-1);dp[0]=0,dp[1]=0;for(int i=2;i<=cost.size();i++)dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);return dp[cost.size()];}
};

优化

其实也不需要把所有的结果全都给记住，只需要记住i的前一个i-1（b）和前前一个i-2（a）

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//a=dp[0],b=dp[1]int a=0,b=0;for(int i=2;i<=cost.size();i++){int c=min(a+cost[i-2],b+cost[i-1]);a=b;b=c;} //c=dp[i] a=dp[i-1] b=dp[i]然后下一次循环的时候i++，a就变成dp[i-2],b变成dp[i-1]return b;}
};

选或不选

0-1背包 完全背包_哔哩哔哩_bilibili

01背包（模板，可以配合该视频和代码随想录博客一起看）

恰好装这个容量，求方案数量的最大最小价值和，那就是把选最大值的操作换成加号

494. 目标和 - 力扣（LeetCode）

后续如果做到了其他的变形题目会同步更新到这里

第一步：回溯法（深度优先遍历）

思路：

配合视频一起看更棒

0-1背包 完全背包_哔哩哔哩_bilibili

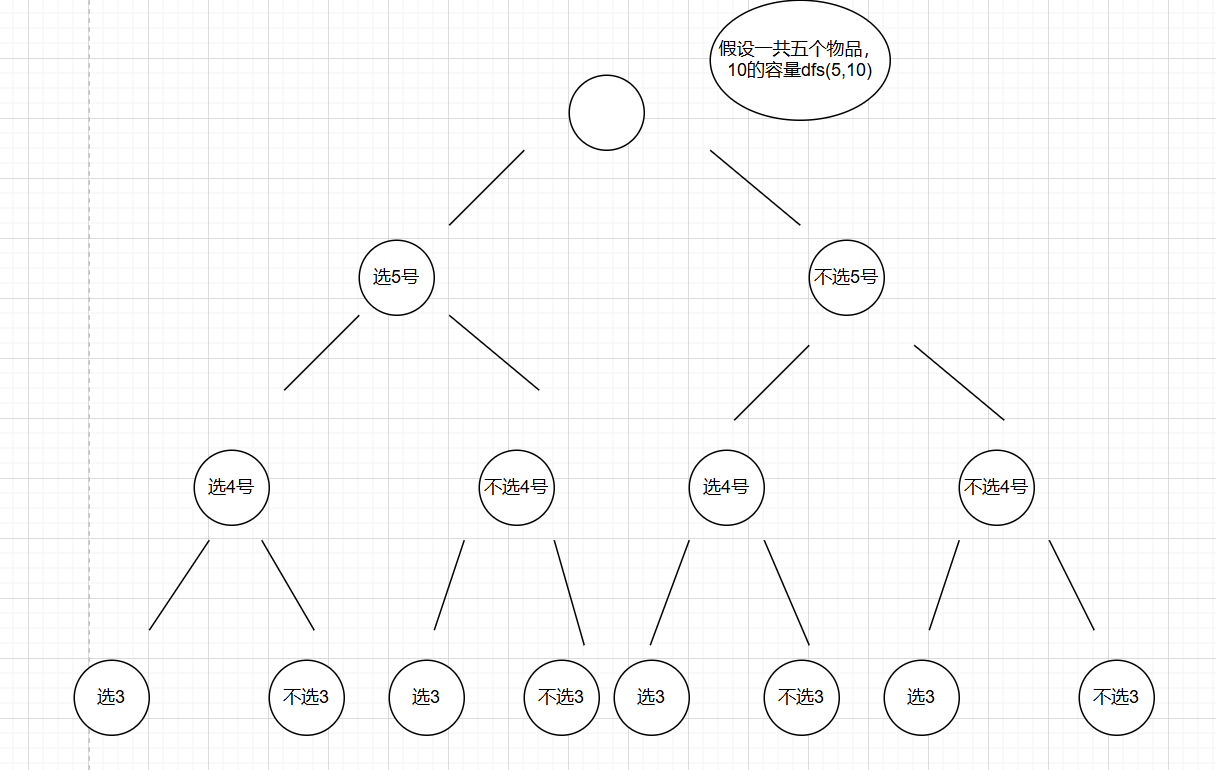
下面的就不画了，大家知道这个意思就行

选编号为i的话就是返回dfs(i-1,c-w[i])+v[i]，就是代表已经把编号为i的物品已经放入了背包（表现为容量减了w[i]，价值加了v[i]），然后继续递归下一个物品

不选编号为i的话就是返回dfs(i-1,c)，这个代表的是一共有i-1个物品，总共是c的容量，那背包能装的最大价值是多少

我们本层函数会产生两个递归，一个是选了i，一个是没选i，返回的都是对应情况的最大值，我们要选最大的，所以要在这两个里面再选一个更大的作为返回值返回

从而得出了递推公式。

这个虽然过不了，时间复杂度太高，但是这是学习动态规划的必由之路

1.返回值和参数

w各个物品所占空间

v各个物品价值

i遍历物品

c是当前剩余的容量

返回值返回选或不选编号为i的物品的最大值

int dfs(vector<int>& w,vector<int>& v,int i,int c)

2.终止条件

if(i<0)return 0;
if(c<w[i])return dfs(w,v,i-1,c);

如果编号小于0说明已经到了树形结构最下面了，要开始从第一个物品选了，即自底（第一个物品）向上（i依次增大）开始遍历

如果当前容量已经小于要选的物品，那就直接返回给上层不选i号物品的结果

3.本层逻辑

在选和不选当前物品两种情况中（只要返回回来的一定是最大值），挑一个更大的返回

return max(dfs(w,v,i-1,c),dfs(w,v,i-1,c-w[i])+v[i]);

完整代码：

class Solution {
public:int dfs(vector<int>& w,vector<int>& v,int i,int c){if(i<0)return 0;if(c<w[i])return dfs(w,v,i-1,c);return max(dfs(w,v,i-1,c),dfs(w,v,i-1,c-w[i])+v[i]);}int 01knapsack(vector<int>& nums,int c) {vector<int> w(nums.begin(),nums.end());vector<int> v(nums.begin(),nums.end());return dfs(w,v,nums.size()-1,c);}
};

C++还可用lambda来写

class Solution {
public:int 01knapsack(vector<int>& nums,int c) {vector<int> w(nums.begin(),nums.end());vector<int> v(nums.begin(),nums.end());function<int(int,int)> dfs=[&](int i,int c)->int{if(i<0)return 0;if(c<w[i])return dfs(i-1,c);return max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i]);};return dfs(nums.size()-1,c);}
};

第二步：改成记忆化搜索

注意，在递归函数中，我们同时有物品编号i和容量c，所以要用一个二维数组作为哈希表来存储计算结果进行复用。

然后在每次返回结果前都赋值一下，把计算结果给存储起来

完整代码：

class Solution {
public:int dfs(vector<int>& w,vector<int>& v,int i,int c,vector<vector<int>>& dp){if(i<0)return 0;if(dp[i][c]!=-1)return dp[i][c];if(c<w[i])return dp[i][c]=dfs(w,v,i-1,c,dp);return dp[i][c]=max(dfs(w,v,i-1,c,dp),dfs(w,v,i-1,c-w[i],dp)+v[i]);}int 01knapsack(vector<int>& nums,int c) {vector<int> w(nums.begin(),nums.end());vector<int> v(nums.begin(),nums.end());vector<vector<int>> dp(nums.size(),vector<int>(c+1,-1));return dfs(w,v,nums.size()-1,c,dp);}
};

class Solution {
public:int 01knapsack(vector<int>& nums,int c) {vector<int> w(nums.begin(),nums.end());vector<int> v(nums.begin(),nums.end());vector<vector<int>> dp(nums.size(),vector<int>(c+1,-1));function<int(int,int)> dfs=[&](int i,int c)->int{if(i<0)return 0;if(dp[i][c]!=-1)return dp[i][c];if(c<w[i])return dp[i][c]=dfs(i-1,c);return dp[i][c]=max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i]);};return dfs(nums.size()-1,c);}
};

第三步：一比一翻译成动态规划(递推)

1.确定dp数组以及下标的含义

二维数组，dp[i][c]就是第i个物品在容量为c时可以取到的最大价值

i是物品编号

c是当前背包的总容量

2.确定递推公式

对应回溯算法本层逻辑部分

选或者不选第i号物品，如果没选，那就和上一个物品第i-1件遍历到j时一样的价值，因为没有选第i号

如果选了那就是 第i-1件物品在j-w[i]时的价值+选择的第i件物品的价值v[i]

dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);

3.dp数组如何初始化

全都初始化为0

第一行在容量大于第一件物品所需容量的时候就当做把第一件给放了进行初始化

因为dp[0][i]的物品编号只有0，即第一件物品，所以只能选择第一件物品得到最大价值，不选的话价值就为0

vector<vector<int>> dp(nums.size(),vector<int>(c+1,0));
for(int i=w[0];i<=c;i++)dp[0][i]=v[0];

4.确定遍历顺序

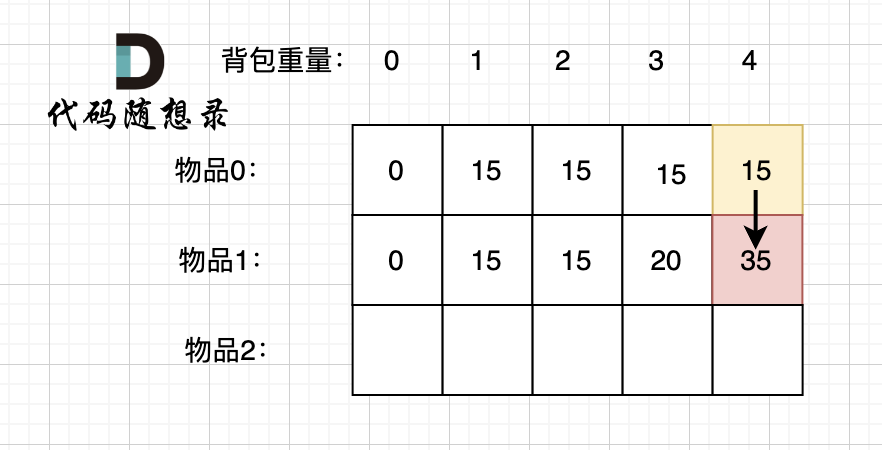
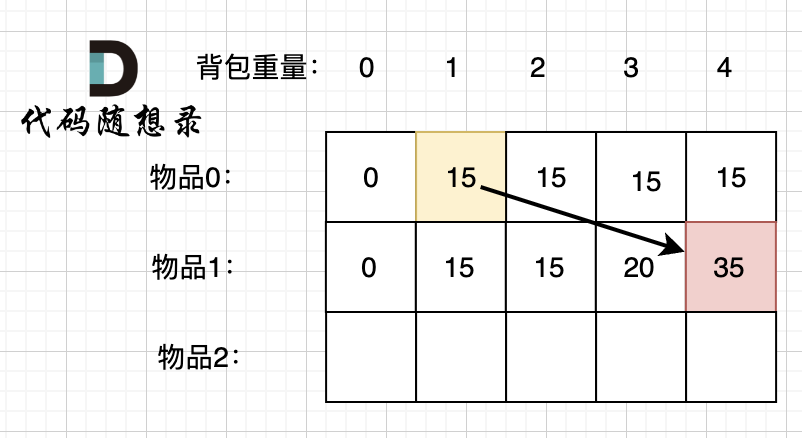
从前往后遍历，先遍历物品或者先遍历容量都是可以的，因为先物品是按照行一行一行来遍历，递推公式中的两个值都可以在遍历得出来，按照容量一列一列遍历也同样可以得出来这两个值

但仅限于二维，如果是一维那就只能先遍历物品后遍历容量，而且只能从后往前遍历容量

因为递推公式中用到的两个值在一维中变成了这样：

vector<int> dp(c+1,0);
for(int i=0;i<nums.size();i++)for(int j=c;j>=w[i];j--)dp[j]=max(dp[j],dp[j-w[i]]+v[i]);

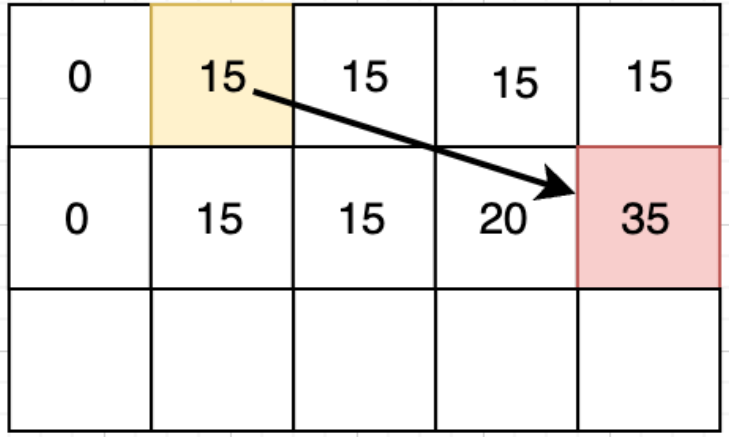
第一行是刷新前的数组，第二行是要对第一行进行覆盖的值，通过第一行的dp[j]和dp[j-w[i]]这两个值进行更新

如果从前往后，那dp[j-w[i]]就会被覆盖，从而得到一个错误的答案

如果不太理解可以转至：代码随想录

0-1背包 完全背包_哔哩哔哩_bilibili视频里面也会讲到滚动数组相关

for(int i=1;i<nums.size();i++)
for(int j=0;j<=c;j++)if(j>w[i])dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);elsedp[i][j]=dp[i-1][j];

完整代码：

class Solution {
public:int 01knapsack(vector<int>& nums,int c) {vector<int> w(nums.begin(),nums.end());vector<int> v(nums.begin(),nums.end());vector<vector<int>> dp(nums.size(),vector<int>(c+1,0));for(int i=w[0];i<=c;i++)dp[0][i]=v[0];for(int i=1;i<nums.size();i++)for(int j=0;j<=c;j++)if(j>w[i])dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);elsedp[i][j]=dp[i-1][j];return dp[w.size()-1][c];}
};

滚动数组代码

class Solution {
public:int 01knapsack(vector<int>& nums,int c) {vector<int> w(nums.begin(),nums.end());vector<int> v(nums.begin(),nums.end());vector<int> dp(c+1,0);for(int i=0;i<nums.size();i++)for(int j=c;j>=w[i];j--)dp[j]=max(dp[j],dp[j-w[i]]+v[i]);return dp[c];}
};