【优选算法】——二分查找!
目录
1、二分查找
2、在排序数组中查找元素的第一个和最后一个位置
3、搜索插入位置
4、x的平方根
5、山脉数组的封顶索引
6、寻找峰值
7、寻找旋转排序数组中的最小值
8、点名
9、完结散花
1、二分查找
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。
示例 1:输入:nums= [-1,0,3,5,9,12],target= 9 输出: 4 解释: 9 出现在nums中并且下标为 4示例 2:
输入:nums= [-1,0,3,5,9,12],target= 2 输出: -1 解释: 2 不存在nums中因此返回 -1
题解:这个题目我们只要用到朴素版的二分查找算法即可!
解题代码:
class Solution {
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;//防溢出if(nums[mid]==target) return mid;else if(nums[mid]<target) left=mid+1;else right=mid-1;}return -1;}
};2、在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]示例 3:
输入:nums = [], target = 0 输出:[-1,-1]

解题代码:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if(nums.empty()) return {-1,-1};//处理边界情况vector<int> ret;int left=0,right=nums.size()-1;//求左端点while(left<right)//判断条件一定是<,如果<=则会进入死循环{int mid=left+(right-left)/2;//不能加1,否则死循环if(nums[mid]<target) left=mid+1;else right=mid;}ret.push_back(nums[right]==target?right:-1);//求右端点left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;//一定要加1,否则死循环if(nums[mid]>target) right=mid-1;else left=mid;}ret.push_back(nums[left]==target?left:-1);return ret;}
};3、搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为
O(log n)的算法。示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
解题代码:
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;//求左端点while(left<right){int mid =left+(right-left)/2;if(nums[mid]>=target) right= mid;else left=mid+1;}return nums[left]<target?left+1:left;}
};4、x的平方根
给你一个非负整数
x,计算并返回x的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如
pow(x, 0.5)或者x ** 0.5。示例 1:
输入:x = 4 输出:2示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
解题代码:
class Solution {
public:int mySqrt(int x) {//求右端点long long left=0,right=x;while(left<right){long long mid=left+(right-left+1)/2;if(mid*mid<=x) left=mid;else right=mid-1;}return left;}
};5、山脉数组的封顶索引
给定一个长度为
n的整数 山脉 数组arr,其中的值递增到一个 峰值元素 然后递减。返回峰值元素的下标。
你必须设计并实现时间复杂度为
O(log(n))的解决方案。示例 1:
输入:arr = [0,1,0] 输出:1示例 2:
输入:arr = [0,2,1,0] 输出:1示例 3:
输入:arr = [0,10,5,2] 输出:1

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left=0,right=arr.size()-1;//求最右端点while(left<right){int mid=left+(right-left+1)/2;if(arr[mid]<arr[mid-1]) right=mid-1;else left=mid;}return left;}
};6、寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组
nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设
nums[-1] = nums[n] = -∞。你必须实现时间复杂度为
O(log n)的算法来解决此问题。示例 1:
输入:nums =[1,2,3,1]输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。示例 2:
输入:nums =[1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。

class Solution {
public:int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;//求最右端点while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]<nums[mid-1]) right=mid-1;else left=mid;}return left;}
};7、寻找旋转排序数组中的最小值
已知一个长度为
n的数组,预先按照升序排列,经由1到n次 旋转 后,得到输入数组。例如,原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2]- 若旋转
7次,则可以得到[0,1,2,4,5,6,7]注意,数组
[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。给你一个元素值 互不相同 的数组
nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。

class Solution {
public:int findMin(vector<int>& nums) {int n=nums.size()-1;//处理特殊情况,即未发生旋转,或旋转到原数组if(nums[0]<nums[n]) return nums[0];int left=0,right=n;//求最左端点while(left<right){int mid=left+(right-left)/2;if(nums[mid]<nums[0]) right=mid;else left=mid+1;}return nums[left];}
};8、点名
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组
records。假定仅有一位同学缺席,请返回他的学号。示例 1:
输入: records = [0,1,2,3,5] 输出: 4示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8] 输出: 7

class Solution {
public:int takeAttendance(vector<int>& r) {int end=r.size()-1;//特殊情况处理if(r[end]==end) return end+1;int left=0,right=end;//求最左端点的二分查找while(left<right){int mid=left+(right-left)/2;if(r[mid]>mid) right=mid;else left=mid+1;}return right;}
};其他解法:
>hash映射
class Solution {
public:int takeAttendance(vector<int>& r) {int n=r.size()+1;int hash[10000]={0};for(auto e:r) hash[e]++;for(int i=0;i<n;i++) {if(hash[i]==0)return i;}return n;}
};>位运算
class Solution {
public:int takeAttendance(vector<int>& r) {int ret=0;for(int i=0;i<r.size();i++){ret^=r[i];ret^=i;}return ret^=r.size();}
};>暴力查找
class Solution {
public:int takeAttendance(vector<int>& r) {int ret=0;for(int i=0;i<r.size();i++){if(r[i]!=i) return i;}return r.size();}
};>数学(高斯求和公式)
class Solution {
public:int takeAttendance(vector<int>& r) {int ret=0,sum1=0,sum2=0;for(int i=0;i<r.size();i++){sum1+=r[i];sum2+=i;}return sum2-sum1+r.size();}
};9、完结散花
好了,这期的分享到这里就结束了~
如果这篇博客对你有帮助的话,可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话,可以点点关注,避免找不到我了呢~
我们下期不见不散~~


相关文章:

【优选算法】——二分查找!
目录 1、二分查找 2、在排序数组中查找元素的第一个和最后一个位置 3、搜索插入位置 4、x的平方根 5、山脉数组的封顶索引 6、寻找峰值 7、寻找旋转排序数组中的最小值 8、点名 9、完结散花 1、二分查找 给定一个 n 个元素有序的(升序)整型数组…...

leetcode hot100【LeetCode 300. 最长递增子序列】java实现
LeetCode 300. 最长递增子序列 题目描述 给定一个未排序的整数数组 nums,找出其中最长递增子序列的长度。 要求: 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如࿰…...

sql注入——靶场Less1
?id1 ?id99union select 1,2,3-- 查看占位 ?id1 order by 3-- 尝试出表有几列 ?id1 order by 4-- 说明只有三列 ?id99 union select 1,database(),3-- 查询当前使用的数据库的名称 ?id99 union select 1,group_concat(table_name),3 from information_schema.tables …...
)
docker file容器化部署Jenkins(一)
Jenkins Github地址:https://github.com/jenkinsci/jenkins 国内镜像地址:https://docker.aityp.com/ 准备工作 # 创建持久化卷目录 mkdir /data/jenkins_home/Jenkins拉取镜像 # 由于Jenkins需要JDK,所以直接拉取带有JDK的Jenkins镜像 doc…...

ArkTS组件继承的高级用法
在HarmonyOS应用开发中,ArkTS作为开发语言,组件的继承是实现代码复用和扩展功能的重要机制。本文将详细介绍ArkTS中组件继承的高级用法,包括继承的概念、如何使用继承、以及继承在实际开发中的应用和最佳实践。 继承的概念 继承是面向对象编…...

第十二章 spring Boot+shiro权限管理
学习目标 引入依赖配置Shiro设计数据库表编写Mapper、Service和Controller前端页面测试与调优其他注意事项 Spring Boot与Shiro的集成是一种常见的Java Web应用程序权限管理解决方案。Shiro是一个强大的Java安全框架,提供了认证、授权、会话管理、加密等安全功能。以…...
jmeter基础01-3_环境准备-Linux系统安装jdk
Step1. 查看系统类型 打开终端,命令行输入uname -a,显示所有系统信息,包括内核名称、主机名、内核版本等。 如果输出是x86_64,则系统为64位。如果输出是i686 或i386,则系统为32位。 Step2. 官网下载安装包 https://www…...

数字证书的简单记录
CA(Certificate Authority):即数字证书颁发认证机构。 CA数字证书(crt/cer证书):数字证书 申请者与颁发者信息申请者公钥颁发者签名,由CA机构使用私钥签名得到数字证书。 CA中间证书࿱…...
ssm基于SSM的校内信息服务发布系统的设计与实现+vue
系统包含:源码论文 所用技术:SpringBootVueSSMMybatisMysql 免费提供给大家参考或者学习,获取源码看文章最下面 需要定制看文章最下面 目 录 摘要 1 Abstract 1 目 录 2 1绪论 4 1.1研究背景与意义 4 1.2国内外研究现状 4 1.3研究…...

Java 教程简介
Java 教程简介 Java 是 Sun Microsystems 公司于 1995 年 5 月推出的一种面向对象的编程语言和运行平台,由 James Gosling 和他的同事共同研发。当前,这个产品已被 Oracle 公司所收购。这篇教程将带你了解 Java 的一些基础知识和应用。 Java 系统简介 …...
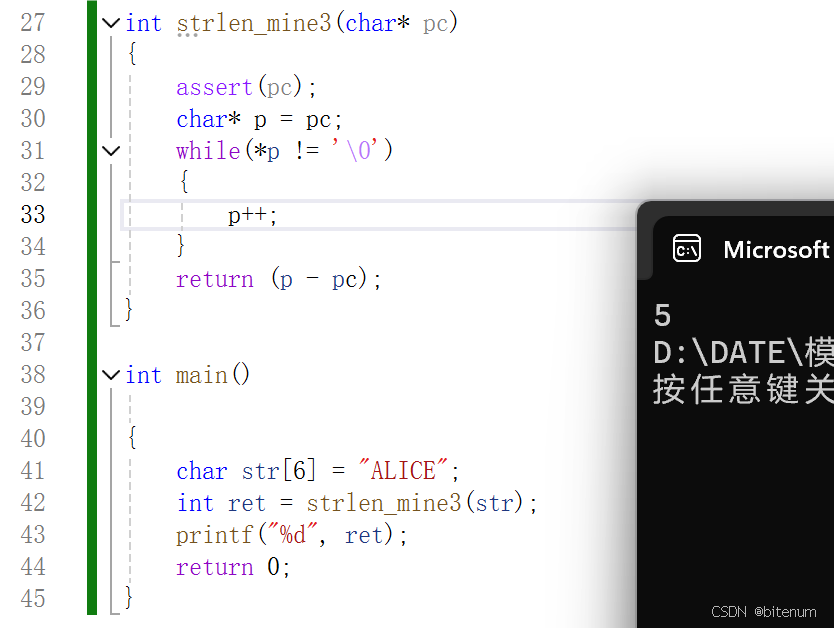
【C/C++】【三种方法】模拟实现strlen
学习目标: 使用代码模拟实现strlen。 逻辑: strlen 需要输入一个字符串数组类型的变量,并且返回一个整型类型的数据。strlen 需要计算字符串数组有多少个元素。 代码1:使用计数器 #define _CRT_SECURE_NO_WARNINGS 1 #include&…...

外贸平台开发多语言处理的三种方式
随着全球贸易的不断增长,外贸平台的多语言处理已成为提升用户体验和市场竞争力的重要因素。在开发外贸平台时,有多种方法可以实现多语言支持。本文将探讨三种主要的多语言处理方式:数据库级多语言支持、前端国际化框架以及内容管理系统&#…...

学习GCC
浅显易懂的GCC使用教程——初级篇_gcc -ddebug-CSDN博客 本文摘抄学习自上面的文章! GCC: GNU Compiler Collection: GNU编译器套件,属于一种编程语言编译器,其原名为GCC(GNU C Compiler),即GNU c语言编译器,虽然缩写…...

B2109 统计数字字符个数
B2109 统计数字字符个数 #include <iostream> using namespace std; # include <string.h> #include <ctype.h> #include <algorithm> int main(){ char str[256]; cin.getline(str,256); //fgets(str,256,stdin); int cnt 0; //for(size_t i 0…...

springboot Lark扫码登录
登录流程 测试通过的地址: https://open.larksuite.com/open-apis/authen/v1/index?app_idcli_a7add3c5bb38902f&redirect_urihttp%3A%2F%2Fstrongculture.cn&stateSTATE...

中专女生数赛疑云:阿里蒙冤,学校之过,尽显世态炎凉
11月3日,阿里巴巴全球数学竞赛组委会发布2024阿里巴巴全球数学竞赛有关情况说明:在本届竞赛中,江苏省涟水中等专业学校教师王某某和其指导的学生入围决赛,引发社会关注。根据决赛阅卷结果,二人未获奖。据调查了解&…...

【neo4j】 图数据库neo4j cypher单一语句 optional 可选操作的技巧
neo4j cypher单一语句 optional 可选操作的技巧 参考文章: Optional merge on relationships Cyper Merge on Optional Match 背景: 使用 match some node 中间还有一些可能与此node有联系的关系或者节点需要处理 create/merge/delete MATCH (src:SOU…...

ip地址分为几大类-IP和子网掩码对照表
一、IP地址的基本概念与分类 IP地址是用于在网络中标识每个设备的逻辑地址。互联网协议将IP地址分为A、B、C、D和E五类,其中A、B、C三类最常用,它们主要根据地址的首位位数以及用途进行划分。 A类地址: 范围:0.0.0.0 - 127.255.2…...

第四篇: 用Python和SQL在BigQuery中进行基础数据查询
用Python和SQL在BigQuery中进行基础数据查询 在大数据分析领域,Google BigQuery 提供了一种快速且经济高效的数据处理方式。对于想要使用SQL查询大规模数据的读者来说,BigQuery的公共数据集资源丰富、操作简便,是学习和实践SQL基础操作的理想…...

OpenCV中使用EdgeDrawing模块查找圆
从OpenCV4.5.2开始,Contrib模块中封装了开源库ED_Lib用于查找图像中的直线、线段、椭圆和圆。Github地址: https://github.com/CihanTopal/ED_Lib 算法原理简介: 边缘绘制(ED)算法是一种解决边缘检测问题的主动方法…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...








