数据结构--二叉树_链式(下)
实现链式结构二叉树
链式结构就是由一个一个的节点组成。

⽤链表来表⽰⼀棵⼆叉树,即⽤链来指⽰元素的逻辑关系。 通常的⽅法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别⽤来给出该结点左孩⼦和右孩⼦所在的链结点的存储地址。
二叉树节点结构的定义
typedef char BTDataType;
//二叉树结点结构的定义
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;关于二叉树的遍历
想要实现链式结构二叉树,就一定要掌握二叉树的遍历相关的知识,二叉树的遍历分为前序遍历,中序遍历和后序遍历。
前序遍历:访问顺序为:根结点、左⼦树、右⼦树(根左右)。
假如,我现在有下图二叉树,那么前序遍历的顺序就为:
A,B,D,NULL,NULL,NULL,C,E,NULL,NULL,F,NULL,NULL.
我们从A开始遍历,A是根他的左孩子是B,但在左子树中,B也是根,继续往下遍历,他的左孩子是d,D与B同理,我们继续往下遍历NULL为空,然后我们就往上走,D的左孩子遍历完成后,我们遍历D的右孩子也是NULL,那么此时,对于D这颗左子树我们已经便利完成,再继续往上走B这颗子树的左孩子和根节点我们已经遍历完成,就剩下它的右孩子NULL,此时整个左子树我们都遍历完成了,再去遍历右子树。右子树与左子树同理,便利的顺序为C,E,BULL,NULL,F,NULL,NULL。如果大家还有不懂,可以在评论区问我,这里就不再赘述了。

中序遍历:访问顺序为:左⼦树、根结点、右⼦树(左根右)。
假如,我现在有下图二叉树,那么中序遍历的顺序就为:
NULL, D, NULL, B, NULL, A, NULL, E, NULL, C, NULL, F, NULL.

后序遍历:访问顺序为:左⼦树、右⼦树,根结点(左右根)。
假如,我现在有下图二叉树,那么后序遍历的顺序就为:
NULL, NULL, D, NULL, B, NULL, NULL, E, NULL, NULL, F, C, A.

了解二叉树的遍历后,我来代码实现一下。开启递归的暴力美学!
老规矩,我们创建三个项目分别是Tree.h,Tree.c,test.c
首先,我们先手动实现一个二叉树:
代码:test.c
//手动构造一棵二叉树
BTNode* CreateTree()
{BTNode* nodeA = buyNode('A');BTNode* nodeB = buyNode('B');BTNode* nodeC = buyNode('C');BTNode* nodeD = buyNode('D');BTNode* nodeE = buyNode('E');BTNode* nodeF = buyNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA;
}前序遍历代码实现:
//前序遍历 根左右
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PreOrder(root->left);PreOrder(root->right);
}前序遍历的过程:
前序遍历的顺序为根左右,我们首先要判断根是不是空,如果根为空我们就不需要遍历了,如果根不为空,我们就要先把根打印出来,打印完成后,我们就又要递归调用root->left,也就是B,B这个节点不为空,我们把B的左孩子D打印出来,打印完成后继续递归,D的左孩子,D的左孩子为空,就满足root=NULL这个条件,打印一下NULL,打印完成后return,return就意味函数栈帧将会释放,也就意味4这个代码执行完了,我们回到上一级3,D的左孩子打印完了,继续递归打印右孩子。此刻,D的左右孩子和它自己都已经打印完成,就意味着D这个函数已经调用完了,我们就要释放函数栈帧,继续向上走。回到2,继续打印B的右孩子(操作6),打印完NULL后,就要return,释放函数栈帧回到2,B的左右孩子和它自身已经打印完了,释放函数栈帧回到A,A的左孩子和它自身打印完了,继续打印它的右孩子C,所以这里的参数root就是C,C不为空,我们接下来打印C里面的数据。递归调用C,打印C的左孩子E,E不为空,我们就打印E里面的数据,E的左孩子为空,我们打印NULL,然后return 释放函数栈帧。然后再去递归E的右孩子,E的右孩子也是空,所以再打印一个NULL。E的左右孩子和它本身都打印成功后,释放函数栈帧,返回C,继续递归C的右孩子F,与E同理,递归完F后,释放函数栈帧回到C,C的全部内容也打印完成,现在要销毁函数栈帧,然后再回到A,A的全部内容也打印完成,也要销毁函数栈帧。A的函数栈帧销毁就意味着我们的遍历完成了,所有通过递归创建的的函数栈帧都销毁完了。

测试结果:

中序遍历代码实现:
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}遍历过程:
首先这里传过来的根节点A,判断A是不是空。不为空就要去递归A。A的左孩子就是是B这个节点,所以这里创建了一个B的函数栈帧,判断B的函数栈帧为空吗,不为空,那我们继续去调用。B的left就是D。所以这里我们创建了一个函数栈帧参数为D,,D不为空再继续去递归它的左孩子在这里创建新的函数栈帧,参数为NULL。在参数为NULL的函数栈帧中,参数为空我们就打印空。然后return当前函数栈帧被销毁。销毁之后我们回到根节点D,D的函数栈帧的左孩子我们已经递归完了,接下来我们要打印一下D,D打印完了之后,接下来我们要递归调用D的右孩子,那么D的右孩子为NULL,我们就打印一下NULL。打印完了之后要return也就意味着NULL这个函数栈帧我们已经调用完了。然后我们销毁这个函数栈帧,然后再继续回到D这个函数。D这个函数里面所有的代码都已经执行完了那么函数战争要销毁回到了B的函数栈帧。再去递归B的右孩子,我们又要去创建一个参数为NULL的函数栈帧,然后打印NULL,再继续return,销毁函数栈帧回到B。那么B所有内容我们已经递归完了,也就意味着这一行代码就已经执行完了,那么接下来我们要打印当前A节点里的值,然后再继续去递归A的右子树,那么A的的的右子树在这里创建了一个函数栈帧参数为C,C不为空我们就在这个函数栈帧里面继续递归它的左孩子。C的左孩子是E,我们就创建参数为E的函数栈帧,E不为空再继续递归它的左孩子,它的左孩子创建函数栈帧的参数NULL,那我们就打印NULL,然后再让它return,然后销毁NULL这个函数栈帧。在E这个函数栈帧中,它的左孩子已经递归完了,接下来是要打印根节点E。接下来是右孩子,继续递归创建函数栈帧为NULL,再打印NULL然后return,然后让函数栈帧消毁。E的全部内容递归完了,那么就要销毁它的函数栈帧,然后回到C,接下来递归它的右孩子F,F不为空,再继续创建函数栈帧参数NULL,为NULL我就打印NULL。然后直接return,销毁函数栈帧。F的左孩子我已经递归完了,接下来我们要打印一下当前节点里的值F, F打印完了之后,在F这个函数栈帧中继续递归它的它的右孩子,创建一个参数为NULL的函数栈帧然后打印NULL,直接return销毁函数栈帧。回到F,F的全部内容我已经打印完了,再继续往上回溯到C这个函数栈帧,C里面的所有内容都已经递归完成,再继续回溯到A这个函数栈帧中,A的全部内容也处理完了,销毁函数栈帧,至此整个递归完成。

测试结果:

后序遍历代码实现:
后续遍历的过程大家可以自己思考一下,有什么问题打在评论区。
//后序遍历--左右根
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}测试结果:

求二叉树结点的个数
求整个二叉树节点的个数只需要根节点+左子树的节点个数+右子树的节点个数。

左子树又是一颗子树,也分左右子树,所以左子树的节点个数也是 1+左子树的节点个数+右子树的节点个数。右子树同理。这就又是一个递归问题。

代码:
// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root) {if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}测试结果:

求二叉树叶子节点的个数
叶子节点:该节点的左孩子和右孩子都为空

我们依然可以把这个二叉树分成左右子树,然后依次求左子树叶子结点的个数和右子树叶子结点的个数,然后相加。还是使用递归。
代码:
// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}测试结果:

求二叉树第K层结点的个数
假设我们要找的是k=2层结点的个数。首先我们要判断根节点为不为空,不为空我们继续遍历, 我们可以递归让k--,找到我们要找的那一层。然后遍历,让左子树节点的个数+右子树节点的个数,就是第k层总的节点的个数。

代码:
// ⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}测试结果:

求二叉树的深度/高度
注意 : 不平衡的二叉树 的深度按照最大的深度计算 如下图 , 二者的深度都为3.

根节点的层次+左子树和右子树中最大的层次。

代码:
//⼆叉树的深度/⾼度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BinaryTreeDepth(root->left);int rightDep = BinaryTreeDepth(root->right);return 1 + (leftDep > rightDep ? leftDep : rightDep);
}测试结果:

二叉树查找值为x的节点
首先我们需要判断根节点是否为空,不为空我们就进行遍历,使用上述讲过的哪种都可以,这里我们使用先序遍历。先遍历左子树,如果找到了就直接返回,如果没找到就继续遍历右子树。

代码:
// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftFind = BinaryTreeFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BinaryTreeFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}测试结果:

二叉树的销毁
二叉树是由链表组成,而链表是由节点组成,所以我们销毁节点即可,那么我们用什么方法销毁节点呢?
我们可以使用前面讲的后序遍历,边遍历边销毁,那为什么不使用前序遍历或者后序遍历呢?
如果我们的根先被销毁了,是不是就不容易找到它的左右孩子啊,所以我们使用后序遍历。
代码:
// ⼆叉树销毁
void BinaryTreeDestory(BTNode** root) {if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL;
}测试结果:

全部代码
Tree.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef char BTDataType;
//二叉树结点结构的定义
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
//前序遍历
void PreOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后序遍历
void PostOrder(BTNode* root);
// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root);
// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root);
// ⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//⼆叉树的深度/⾼度
int BinaryTreeDepth(BTNode* root);
// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// ⼆叉树销毁
void BinaryTreeDestory(BTNode** root);Tree.c
#include"Tree.h"//前序遍历 根左右
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PreOrder(root->left);PreOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}
//后序遍历--左右根
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}
// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root) {if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
// ⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
//⼆叉树的深度/⾼度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BinaryTreeDepth(root->left);int rightDep = BinaryTreeDepth(root->right);return 1 + (leftDep > rightDep ? leftDep : rightDep);
}
// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftFind = BinaryTreeFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BinaryTreeFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}
// ⼆叉树销毁
void BinaryTreeDestory(BTNode** root) {if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL;
}tese.c
#include"Tree.h"BTNode* buyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->data = x;node->left = node->right = NULL;return node;
}
//手动构造一棵二叉树
BTNode* CreateTree()
{BTNode* nodeA = buyNode('A');BTNode* nodeB = buyNode('B');BTNode* nodeC = buyNode('C');BTNode* nodeD = buyNode('D');BTNode* nodeE = buyNode('E');BTNode* nodeF = buyNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA;
}
void test() {BTNode* root = CreateTree();//PreOrder(root);//InOrder(root);//PostOrder(root);//printf("size:%d\n", BinaryTreeSize(root));//printf("leaf size:%d\n", BinaryTreeLeafSize(root));//printf("K size:%d\n", BinaryTreeLevelKSize(root, 2));//printf("K size:%d\n", BinaryTreeLevelKSize(root, 3));//printf("depth:%d\n", BinaryTreeDepth(root));BTNode* find = BinaryTreeFind(root, 'Z');if (find == NULL){printf("未找到!\n");}else {printf("找到了!\n");}BinaryTreeDestory(&root);
}
int main() {test();return 0;
}祝大家生活愉快。
相关文章:

数据结构--二叉树_链式(下)
实现链式结构二叉树 链式结构就是由一个一个的节点组成。 ⽤链表来表⽰⼀棵⼆叉树,即⽤链来指⽰元素的逻辑关系。 通常的⽅法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别⽤来给出该结点左孩⼦和右孩⼦所在的链结点的存储…...

unity游戏开发之--人物打怪爆材料--拾进背包的实现思路
unity游戏开发之–人物打怪爆材料–拾进背包的实现思路 游戏实现:unity c# 1、敌人(怪物)的生命值和伤害系统 using UnityEngine; using System.Collections.Generic;public class Enemy : MonoBehaviour {[Header("基础属性")]…...

AWTK文件系统适配器更新-支持RT-Thread DFS POSIX接口
介绍 AWTK 文件系统适配器。 在嵌入式平台中,有时没有 POSIX 兼容的文件系统 API,需要把一些文件系统实现,包装成 AWTK 的 fs 接口。本项目提供一些常见文件系统的适配,目前支持的文件系统有: FATFS 主要用于访问 TF…...
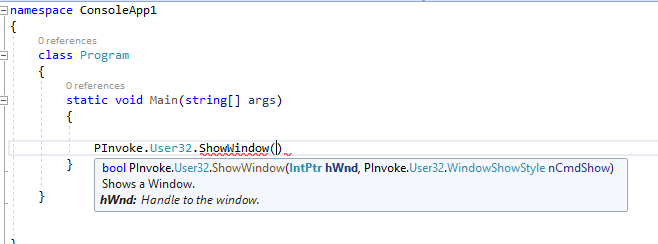
C#如何快速获取P/Invoke方法签名
使用API函数已经好几年了,封装函数签名基本是参照MSDN上的文档,然后再做数据类型对应。 虽然有 pinvoke.net 这个网站,但基本很少使用。一方面是想多动手,另一方面是因为各种数据类型基本都用过了,都能自己在C#中 对应…...

CqEngine添加联合索引和复合唯一索引
一.实体类 Data public class CategoryT {private Integer id;private String oneCategory;private String twoCategory;private String createTime;private String updateTime;public String uniKey() {return oneCategory "/" twoCategory;} }二.集合 Suppress…...
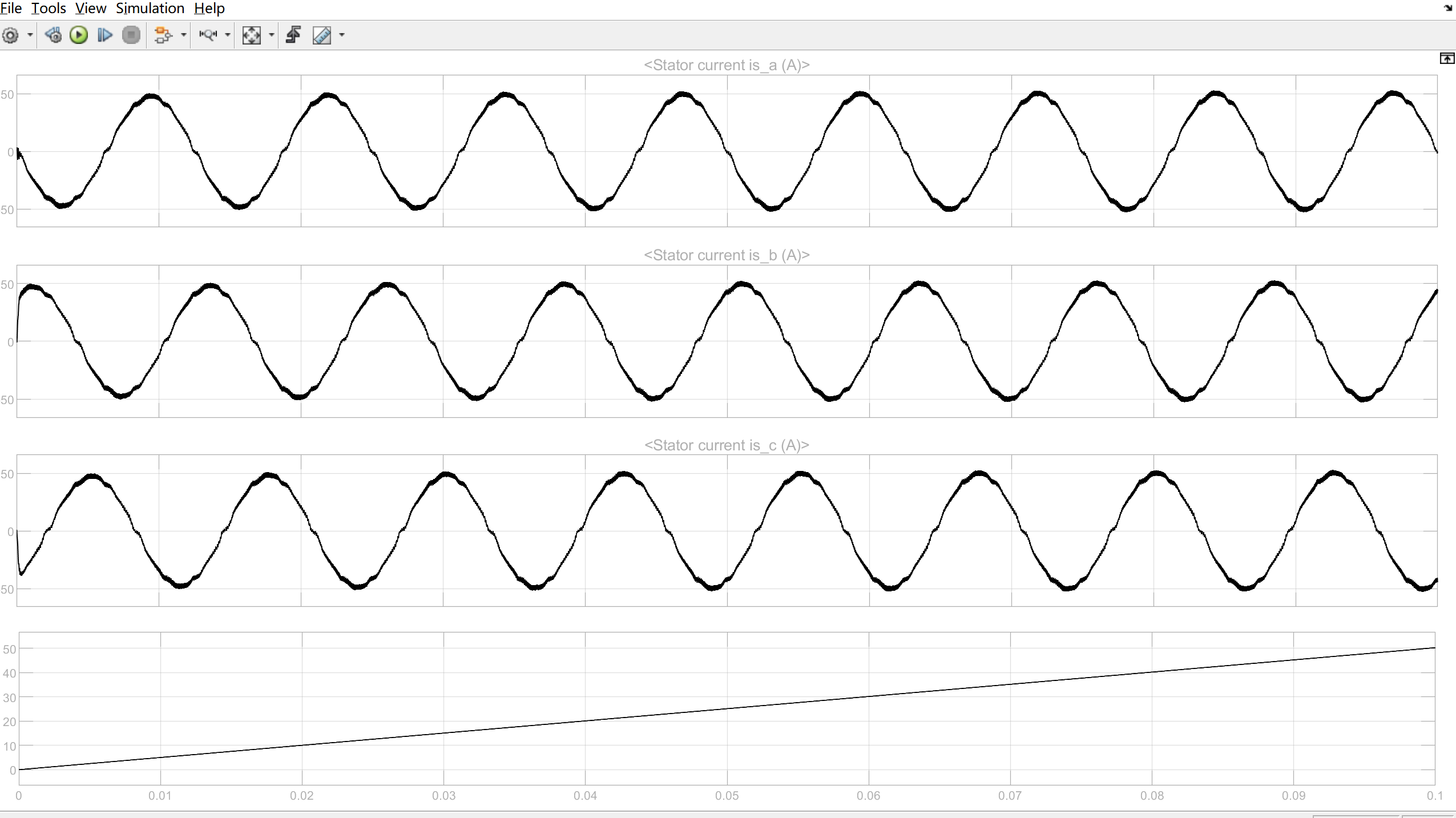
基于matlab的SVPWM逆变器死区补偿算法仿真研究
背景介绍: 三相脉宽调制(pulse width modulation,PWM)电压源逆变器(voltage source inverter,VSI)的死区效应可导致电机相电压和相电流畸变、零电流钳位效应以及转矩和转速脉动,系统性能降低。为提高系统运行性能,对V…...

【网页设计】CSS 定位
目标 能够说出为什么要用定位能够说出定位的4种分类能够说出4种定位各自的特点能够说出为什么常用子绝父相布局能够写出淘宝轮播图布局能够说出显示隐藏的2种方式以及区别 1. 定位 1.1 为什么需要定位 提问: 以下情况使用标准流或者浮动能实现吗?1. …...

scala的属性访问权限
scala的属性访问权限有四种: 默认访问权限;protected访问权限;private访问权限;private[this]访问权限 package Test1104 //访问控制权限// 类的内部方法 伴生对象中的方法 类的外部(对象,访问)…...

QGIS:HCMGIS插件
插件GitHub地址:https://github.com/thangqd/HCMGIS。 以下对HCMGIS插件进行简单介绍,并演示如何进行地图数据下载。 插件简介 HCMGIS - Basemaps, Download OpenData, Batch Converter, VN-2000 Projections, and Field Calculation Utilities for QGI…...

Melty 主体流程图
┌───────────┐ │ 用户输入 │ └─────┬─────┘ │(自然语言或指令) │ ▼ ┌───────────┐ │ 自然语言处理 │ │ (NLU 模块)│ └─────┬─────┘ │ │ 解析用户意图 │ ▼ ┌─…...
【图像与点云融合教程(五)】海康相机 ROS2 多机分布式实时通信功能包
0. 前言 Github 仓库链接:Hikvision Camera ROS2 package 0.1 问题背景 上一篇[博客](【图像与点云融合教程(四)】海康相机 ROS2 功能包 - 古月居 (guyuehome.com))介绍了我开源的海康相机 ROS2 功能包,在本地机器上可以实时订…...

正则截取字符窜数字,字母,符号部分
Testvoid test20() {String str "BJRabG11325F9**0**";// 提取字母部分String letterPart str.replaceAll("[^a-zA-Z]", "");String noLetterPart str.replaceAll("[a-zA-Z]", "");System.out.println("字母部分&am…...

【ChatGPT】让ChatGPT生成跨语言翻译的精确提示
让ChatGPT生成跨语言翻译的精确提示 在跨语言交流中,为了确保翻译的准确性,生成精确的提示(Prompt)来指导ChatGPT翻译内容是至关重要的。无论是要处理复杂的技术术语、俚语,还是保持特定的语言风格,使用有…...

Vue3父传子
1. App.vue - 父组件 咱们先来看左边的 App.vue,它扮演的是“父亲”角色——你可以想象它是一位热心的老爸,手里拿着一条消息,正准备把这条消息送到“儿子”那里。 <script setup> // 这个 setup 就像一个神奇的开关,一开…...

使用VBA宏合并多个Excel文件的Sheet页
使用VBA宏合并多个Excel文件的Sheet页 在日常的Excel数据处理工作中,我们经常需要将多个Excel文件中的工作表合并到一个Excel文件中。这种操作可以极大地提高数据处理效率,但如果文件数量较多,手动合并会非常繁琐。本文将介绍如何使用VBA宏来…...

Anolis8防火墙安全设置
一、账号安全 1、禁止root远程登录 首先创建一个普通用户,然后修改系统配置禁止root登录,因为root作为系统默认的超级管理员,权限过大,日常操作使用易导致安全风险。 1.1、首先要建立一个新的登录用户 useradd username #增…...

标题:自动化运维:现代IT运维的革新力量
标题:自动化运维:现代IT运维的革新力量 随着信息技术的飞速发展,企业对于IT系统的依赖日益加深,运维工作的重要性也愈发凸显。传统的运维模式,往往依赖于人工操作,效率低下且容易出错,难以满足…...

无人机之姿态融合算法篇
无人机的姿态融合算法是无人机飞行控制中的核心技术之一,它通过将来自不同传感器的数据进行融合,以实现更加精确、可靠的姿态检测。 一、传感器选择与数据预处理 无人机姿态融合算法通常依赖于多种传感器,包括加速度计、陀螺仪、磁力计等。这…...

Redis系列---数据管理
目录标题 数据类型String优点缺点底层结构使用场景实际使用 List优点缺点底层结构使用场景实际使用 Hash优点缺点底层结构使用场景实际使用 Set优点缺点底层结构使用场景实际使用 Zset优点缺点底层结构使用场景实际使用 HyperLogLog优点缺点底层结构使用场景实际使用 GEO优点缺…...

【Linux系统编程】第四十二弹---多线程编程全攻略:涵盖线程创建、异常处理、用途、进程对比及线程控制
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】【Linux系统编程】 目录 1、线程创建 2、线程异常 3、线程用途 4、进程 VS 线程 5、线程控制 5.1、创建和等待线程 1、线程创建 线程能看到进程的大…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
