推荐一款面向增材制造的高效设计平台:nTopology
nTopology是一款面向增材制造的高效设计平台,平台预置了大量增材制造常用的设计工具包,工程师通过调用若干个预置工具包、或自主开发定制的工具包,建立一个工作流,实现复杂几何结构的参数化设计。nTopology集合了的强大几何建模和仿真分析功能,并充分考虑增材制造的工艺特点,能够帮助工程师快速掌握面向增材制造的设计方法,充分发挥增材制造带来的广阔自由度,同时可重复使用的工作流使得设计流程自动化,大大提高设计效率。
nTopology 的核心是我们的隐式建模引擎。在隐式建模中,每个实体都由一个数学方程式描述。nTopology 牢不可破的几何引擎可实现闪电般快速的设计迭代,并消除高级产品开发中的设计瓶颈。

软件特点
完全控制您的设计工作流程
没有“黑匣子”。nTopology 让您可以完全控制生成工作流、优化过程及其输出的各个方面。
创建可重复使用的工作流程,根据您的应用程序的独特要求量身定制。使用仿真结果、测试数据、工程公式和现场驱动设计控制空间中每个点的设计。
设计流程
不仅仅是零件
实现超越零件性能的投资回报率。没有人像您一样了解您的流程和行业。
nTopology 是从头开始构建的,使您能够创建自定义应用程序来满足您的特定需求并转变您开发创新产品的方式。
使用 GPU 加速实时更改 有了
GPU 加速,在其他软件中需要几分钟的复杂建模操作在 nTopology 中变得瞬间完成。
使用 nTopology 正在申请专利的硬件加速技术,享受实时反馈和 10 到 100 倍的性能提升,从而节省数天的设计时间。
增材设计的全能选手
nTopology设计平台集成了增材制造结构设计、结构仿真、打印切片等涉及全流程的全套功能,包括基本模块、增材制造模块、蜂窝/多孔材料模块、有限元分析模块、轻量化模块、拓扑优化模块。nTopology采用隐式建模技术,是一种基于数学函数或隐式模型的驱动式设计技术,使nTopology的设计流程具有无与伦比的速度和可靠性。nTopology兼具CAD、CAE和CAM功能,可快速实现创成式设计、轻量化、拓扑优化等创新设计,输出可用于增材制造的产品解决方案。
基本模块:包括数据导入导出、隐式模型转换/创建/特征操作、布尔运算、驱动设计的场(Field)创建、点阵晶格设计等;
增材制造模块:设置打印平台、添加支撑、切片,以及抽壳、晶格填充轻量化设计;
蜂窝/多孔材料模块:变尺寸、变厚度的晶格填充,复杂表面纹理设计,快速生成蜂窝/多孔材料;
有限元分析模块:线性静力、模态、屈曲、稳态热分析、点阵结构均质化材料分析,并支持有限元模型/网格的输出;
轻量化模块:晶格填充、表面加强筋设计、变厚度的抽壳设计等;
拓扑优化模块:考虑增材悬垂角等制造约束,自动几何光顺、重构,基于拓扑优化的材料密度分布自动进行变厚度的点阵晶格设计。
本文来源于:nTopology(增材制造结构设计)v5.9.2免费版-下载集nTopology是一款面向增材制造的高效设计平台,平台预置了大量增材制造常用的设计工具包,工程师通过调用若干个预置![]() https://www.xzji.com/soft/5819.html
https://www.xzji.com/soft/5819.html
相关文章:
推荐一款面向增材制造的高效设计平台:nTopology
nTopology是一款面向增材制造的高效设计平台,平台预置了大量增材制造常用的设计工具包,工程师通过调用若干个预置工具包、或自主开发定制的工具包,建立一个工作流,实现复杂几何结构的参数化设计。nTopology集合了的强大几何建模和…...

SQL,力扣题目1767,寻找没有被执行的任务对【递归】
一、力扣链接 LeetCode_1767 二、题目描述 表:Tasks ------------------------- | Column Name | Type | ------------------------- | task_id | int | | subtasks_count | int | ------------------------- task_id 具有唯一值的列。 ta…...

JavaScript数据类型- Symbol 详解
文章目录 前言1.唯一性2. 描述3. 作为对象属性键4. 全局注册6. 不可变性7. 隐式转换 前言 Symbol是ES6新增内容,代表创建后独一无二且不可变的数据类型,它主要是为了解决可能出现的全局变量冲突的问题 在JavaScript发展的过程中,其中的ES6带…...

WordPress网站添加嵌入B站视频,自适应屏幕大小,取消自动播放
结合bv号 改成以下嵌入式代码(自适应屏幕大小,取消自动播放) <iframe style"width: 100%; aspect-ratio: 16/9;" src"//player.bilibili.com/player.html?isOutsidetrue&bvidBV13CSVYREpr&p1&autoplay0" scrolling…...

11.6 校内模拟赛总结
打的很顺的一场 复盘 7:40 开题,看到题目名很interesting T1 看起来很典,中位数显然考虑二分,然后就是最大子段和;T2 构造?一看数据范围这么小,感觉不是很难做;T3 神秘数据结构;T…...
)
Redis常用的五大数据类型(列表List,集合set)
简介 List 的特点:单键多值。底层实际是个双向链表,对两端的操作性能很高,通过索引下标的操作中间的节点性能会较差。 Redis 列表是简单的字符串列表,按照插入顺序排序。你可以添加一个元素到列表的头部(左边ÿ…...

Ubuntu 20.04 部署向量数据库 Milvus + Attu
前言 最开始在自己的办公电脑(无显卡的 windows 10 系统) 上使用 Docker Desktop 部署了 Milvus 容器,方便的很, 下载 Attu 也很方便,直接就把这个向量数据库通过 Attu 这个图形化界面跑了起来,使用起来感…...

实现数传数据转网口(以太网)和遥控器SBUS信号转串口的功能
为了帮助你实现数传数据转网口(以太网)和SBUS信号转串口的功能,这里提供一个基本的框架。我们将使用STM32微控制器来完成这些任务。假设你已经具备了STM32的基本开发经验,并且已经安装了相应的开发环境(如STM32CubeIDE…...

APP 后台广告位配置的关键要素与策略
在当今数字化营销的浪潮中,APP 作为重要的信息传播渠道,其后台广告位的配置显得尤为关键。这不仅影响着广告的展示效果,还直接关系到用户体验和平台收益。 首先,了解目标受众是配置广告位的基础。通过对 APP 用户的行为数据进行分…...

分布式数据库概述
分布式数据库概述 分布式数据库是一种将数据分散存储在多个物理节点上的数据库系统,这些节点通过网络相互连接,形成一个逻辑上统一的数据库系统。它旨在提高数据的可用性、可靠性、性能和可扩展性,是现代大数据和云计算环境下不可或缺的重要技术。 一、分布式数据库的核心…...

用通义灵码帮助实现校验bpmn.js当前画布上只能有一个开始节点的功能
最终代码: const elementRegistry this.bpmnModeler.get(elementRegistry);// 获取所有元素const allElements elementRegistry.getAll();// 过滤出开始节点const startEvents allElements.filter(element > element.type bpmn:StartEvent);// 校验开始节点的…...

OKHTTP断点续传
OKHTTP断点续传 文章目录 OKHTTP断点续传HTTP断点续传知识点RangeContent RangeEtag&If-Range(文件唯一标志) OKHTTP断点下载OKHTTP 简单短断点下载代码示例 Android 断点续传一直是面试的高频问点,这里从HTTP断点续传知识和Android续传思…...

软件测试学习笔记丨Flask操作数据库-ORM
本文转自测试人社区,原文链接:https://ceshiren.com/t/topic/23426 什么是持久化 是把数据保存到可永久保存的存储设备中(比如磁盘)。持久化的主要应用是将内存中的数据存储在关系型数据库中,当然也可以存储在磁盘文件…...
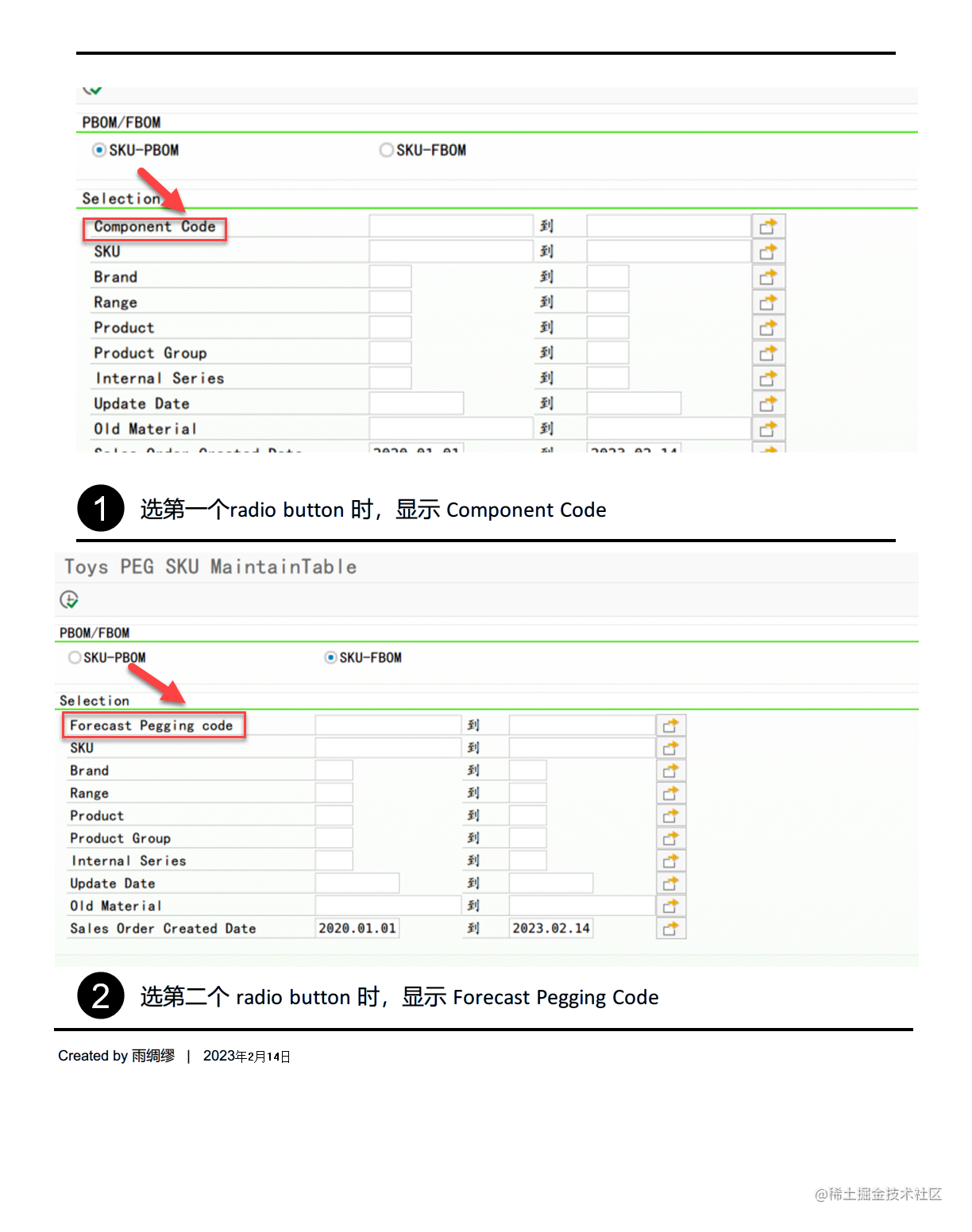
ABAP 开发的那些小技巧
在对话框程序中的选择屏幕添加图标 要在选择屏幕中添加图标,其中包括参数: 在参数的选择文本中或选择选项(select-option)中写入 01 或选择选项: 您可以使用 01、02、03,依此类推,以获取不同的不同图标。 在运行时…...

电科金仓(人大金仓)更新授权文件(致命错误: XX000: License file expired.)
问题:电科金仓(人大金仓)数据库链接异常,重启失败,查看日志如下: 致命错误: XX000: License file expired. 位置: PostmasterMain, postmaster.c:725 解决方法: 一、下载授权文件 根据安装版本在官网下载授权文件(电科金仓-成为世界卓越的数据库产品与服务提供商)…...

玩转「HF/魔搭/魔乐」平台
模型下载 Hugging Face 下载到 GitHub CodeSpace CodeSpace创建环境: # 安装transformers pip install transformers4.38 pip install sentencepiece0.1.99 pip install einops0.8.0 pip install protobuf5.27.2 pip install accelerate0.33.0下载internlm2_5-7b…...

鸿蒙系统的优势 开发 环境搭建 开发小示例
HarmonyOS是面向多智能终端、全场景的分布式操作系统,为消费者提供跨终端的无缝体验.华为开发者联盟从HarmonyOS应用设计、开发、测试、推广变现等环节全方位助力开发者。 开发者可以通过以下步骤学习鸿蒙系统的开发: 基础理论学习: 了解鸿蒙系统概述&a…...

python批量合并excel文件
当工作中发现有多个excel表需要进行相同的操作或者需要汇总在一起,一个一个处理太费时间,以下的python代码能够帮你解决这个问题~ import pandas as pd import os# 设置Excel文件所在的文件夹路径和合并文件的输出路径 folder_path D:\\Desktop\\dat…...
常用操作)
AWS S3 JavaScript SDK(v3)常用操作
安装 aws s3 sdk npm install aws-sdk/client-s3配置 创建 ~/.aws/credentials 文件,添加以下配置项: [default] aws_access_key_id<...> aws_secret_access_key<...> region<...>S3 SDK常用桶操作 获取桶列表 import {S3Client,…...

数据结构——图的基本操作
文章目录 1.图2.图的结构体定义3.图的初始化4.添加顶点、删除顶点4.1添加顶点4.2删除顶点 5.添加边、删除边5.1添加边5.2删除边 6.打印图7.main函数 在生命旅途中,我们就像是一个个节点,被无数看不见的边相连。每一次的相识与相离,都在这张巨…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
