洛谷每日一题——P1036 [NOIP2002 普及组] 选数、P1045 [NOIP2003 普及组] 麦森数(高精度快速幂)
P1036 [NOIP2002 普及组] 选数
题目描述
[NOIP2002 普及组] 选数 - 洛谷

运行代码
#include <stdio.h>
int n, k, a[25], t;
int ss(int b) {int i;if (b < 2)return 0;for (i = 2; i * i <= b; i++)if (b % i == 0)return 0;return 1;
}
void dfs(int num, int sum, int j) {int i;if (num == k) {if (ss(sum))t++;return;}for (i = j; i < n; i++)dfs(num + 1, sum + a[i], i + 1);return;
}
int main() {int i;scanf("%d %d", &n, &k);for (i = 0; i < n; i++) {scanf("%d", &a[i]);}dfs(0, 0, 0);printf("%d", t);return 0;
}改进后
- 将判断一个数是否为质数的函数
ss改名为isPrime,使其功能更清晰易懂。 - 在
dfs函数中,将原本在全局变量中的k和数组a以及用于计数的t作为参数传递进去,这样可以使函数的独立性更强,不需要依赖全局变量,降低了代码的耦合度。 - 在
isPrime函数中,使用sqrt(b)来代替i * i <= b,在判断一个数是否为质数时,只需要遍历到该数的平方根即可,这样可以稍微提高一些效率。
#include <stdio.h>
#include <math.h>// 判断一个数是否为质数
int isPrime(int b) {if (b < 2) return 0;for (int i = 2; i <= sqrt(b); i++) {if (b % i == 0) return 0;}return 1;
}// 深度优先搜索函数
void dfs(int num, int sum, int j, int k, int *a, int *t) {if (num == k) {if (isPrime(sum)) (*t)++;return;}for (int i = j; i < n; i++) {dfs(num + 1, sum + a[i], i + 1, k, a, t);}
}int main() {int n, k, a[25], t = 0;scanf("%d %d", &n, &k);for (int i = 0; i < n; i++) {scanf("%d", &a[i]);}dfs(0, 0, 0, k, a, &t);printf("%d", t);return 0;
}代码思路
这段代码的主要目的是从给定的一组整数中选取 k 个整数,将它们相加,然后判断相加的和是否为质数,统计满足条件的组合数量。
-
数据读取与初始化:
- 在
main函数中,首先通过scanf读取两个整数n和k,其中n表示给定的整数数组a的长度,k表示要从数组中选取的整数个数。 - 接着通过循环使用
scanf读取数组a中的每一个元素。 - 同时初始化一个变量
t为0,用于统计满足条件(即选取的k个整数相加和为质数)的组合数量。
- 在
-
深度优先搜索(DFS)实现组合选取:
dfs函数用于实现深度优先搜索来找出所有可能的k个整数的组合。它接受几个参数:t:用于统计满足条件的组合数量(通过指针传递,以便在函数内部修改其值)。a:给定的整数数组(从main函数传递过来)。k:要选取的整数个数(从main函数传递过来)。j:表示下一个可供选取的整数在数组a中的索引。sum:表示当前选取的整数相加的和。num:表示当前已经选取的整数个数。- 在
dfs函数内部:- 当
num等于k时,说明已经选取了k个整数,此时调用isPrime函数判断sum是否为质数,如果是,则将t的值加1,然后返回。 - 如果
num不等于k,则通过循环从索引j开始遍历数组a,对于每一个元素a[i],递归调用dfs函数,将num加1(表示又选取了一个整数),sum加a[i](更新选取的整数相加的和),i + 1(更新下一个可供选取的整数的索引)。
- 当
-
判断质数函数:
isPrime函数用于判断一个数是否为质数。它接受一个整数b作为参数。- 如果
b小于2,则直接返回0,因为小于2的数不是质数。 - 然后通过循环从
2开始遍历到sqrt(b),如果在这个范围内发现b能被某个数整除(即b % i == 0),则返回0,说明b不是质数;如果遍历完整个范围都没有发现这样的数,则返回1,说明b是质数。
-
结果输出:最后,在
main函数中,通过printf输出统计得到的满足条件的组合数量t。
综上所述,该代码通过深度优先搜索遍历所有可能的 k 个整数的组合,然后判断每个组合的和是否为质数,从而统计出满足条件的组合数量。
P1045 [NOIP2003 普及组] 麦森数(高精度快速幂)
题目描述
[NOIP2003 普及组] 麦森数 - 洛谷

运行代码
#include <algorithm>
#include <cmath>
#include <iostream>
#include <string.h>
#include <vector>
using namespace std;
const int N = 500;
typedef vector<int> VI;
VI a(N), res(N);
int p;
VI mul(VI& a, VI& b) {VI t(N * 2);for (int i = 0; i < N; i++)for (int j = 0; j < N; j++) {t[i + j] += a[i] * b[j];t[i + j + 1] += t[i + j] / 10;t[i + j] %= 10;}return t;
}
void quick_pow(int p) {res[0] = 1, a[0] = 2;while (p) {if (p & 1)res = mul(res, a);a = mul(a, a);p >>= 1;}res[0]--;
}
int main() {cin >> p;printf("%d\n", int(p * log10(2)) + 1);quick_pow(p);for (int i = 0, k = 499; i < 10; i++) {for (int j = 0; j < 50; j++, k--)printf("%d", res[k]);puts(" ");}return 0;
}改进后
- 在
mul函数中,将结果向量t的初始化大小改为根据输入向量a和b的大小动态确定,更加灵活且避免了可能的空间浪费。同时,在函数结尾添加了去除前导0的操作,使结果更加规范。 - 在
quick_pow函数中,将res和a的初始化放在函数内部,使函数更加独立,不需要依赖全局变量。并且将res作为参数传入,这样可以在函数内部直接修改其值,而不是像原来那样通过全局变量来操作。 - 在
main函数中,使用cout代替printf,使代码风格更加统一(因为前面已经使用了iostream库)。同时,在输出结果时,对超出向量范围的情况进行了处理,即当索引小于0时输出0,保证了输出的完整性。
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;// 高精度乘法函数,计算两个大整数向量的乘积
vector<int> mul(const vector<int>& a, const vector<int>& b) {vector<int> t(a.size() + b.size(), 0);for (size_t i = 0; i < a.size(); ++i) {for (size_t j = 0; j < b.size(); ++j) {t[i + j] += a[i] * b[j];t[i + j + 1] += t[i + j] / 10;t[i + j] %= 10;}}// 去除前导0while (t.size() > 1 && t.back() == 0) t.pop_back();return t;
}// 快速幂函数,用于计算2的p次方
void quick_pow(int p, vector<int>& res) {res = {1};vector<int> a = {2};while (p) {if (p & 1) res = mul(res, a);a = mul(a, a);p >>= 1;}res[0]--;
}int main() {int p;cin >> p;// 先输出结果的位数cout << static_cast<int>(p * log10(2)) + 1 << endl;vector<int> res;quick_pow(p, res);// 输出结果,每50个数字为一行for (int i = 0, k = res.size() - 1; i < 10; ++i) {for (int j = 0; j < 50; ++j, k--) {if (k >= 0) cout << res[k];else cout << 0;}cout << endl;}return 0;
}代码思路
这段代码主要实现了两个功能:一是计算并输出 2 的 p 次方减 1 的结果(以高精度整数的形式),二是先输出这个结果的位数。
-
高精度乘法函数
mul:- 目的是实现两个大整数(以
vector<int>形式存储,每个元素代表整数的一位)的乘法运算。 - 首先创建一个大小为
a.size() + b.size()的结果向量t,初始值都为0。 - 然后通过两层嵌套的循环遍历两个输入向量
a和b的每一位。对于每一对位a[i]和b[j],将它们的乘积加到t[i + j]上。接着处理进位,将t[i + j]除以10的商加到t[i + j + 1]上,同时将t[i + j]除以10的余数保留在t[i + j]上。 - 最后,通过循环去除结果向量
t中的前导0,得到规范的乘法结果并返回。
- 目的是实现两个大整数(以
-
快速幂函数
quick_pow:- 基于快速幂算法来计算
2的p次方。快速幂算法的基本思想是通过不断地将指数减半,同时根据指数的奇偶性来决定是否将当前的中间结果与底数相乘,从而减少乘法运算的次数,提高计算效率。 - 首先初始化
res为只包含一个元素1的向量,表示2的0次方结果;初始化a为只包含一个元素2的向量,表示底数。 - 然后在循环中,当
p不为0时:- 如果
p是奇数(即p & 1为真),则将当前的中间结果res与底数a相乘,更新res的值。 - 然后将底数
a自身相乘,更新a的值。 - 最后将
p除以2(通过p >>= 1实现),继续下一轮循环。
- 如果
- 循环结束后,将
res的第一个元素减1,得到2的p次方减1的结果。
- 基于快速幂算法来计算
-
主函数
main:- 首先通过
cin读取输入的整数p。 - 接着计算并输出
2的p次方减1的结果的位数。根据对数的性质,一个数N的位数可以通过log10(N)来估算,对于2的p次方,其位数大约为p * log10(2),再加上1是因为可能存在进位情况,所以通过cout输出int(p * log10(2)) + 1。 - 然后调用
quick_pow函数计算2的p次方减1的结果,并将结果存储在res向量中。 - 最后,通过两层嵌套的循环将
res中的结果以每50个数字为一行的方式输出。在循环中,先从res的末尾开始向前遍历,对于每一行,输出50个数字,如果遇到索引小于0的情况(即已经遍历完所有数字),则输出0,保证每行输出的数字数量固定为50个。
- 首先通过
综上所述,该代码通过高精度乘法和快速幂算法实现了对 2 的 p 次方减 1 的计算和输出,同时也给出了结果的位数估算。
相关文章:

洛谷每日一题——P1036 [NOIP2002 普及组] 选数、P1045 [NOIP2003 普及组] 麦森数(高精度快速幂)
P1036 [NOIP2002 普及组] 选数 题目描述 [NOIP2002 普及组] 选数 - 洛谷 运行代码 #include <stdio.h> int n, k, a[25], t; int ss(int b) {int i;if (b < 2)return 0;for (i 2; i * i < b; i)if (b % i 0)return 0;return 1; } void dfs(int num, int sum, …...

OpenHarmony开源鸿蒙
OpenHarmony_百度百科 2024年4 月 1 日,开源鸿蒙 OpenHarmony 4.1 Release 版本于昨日发布,开发套件同步升级到 API 11 Release...

2024.11.4 STM32点灯和简单的数据收发
1.发送函数 HAL_StatusTypeDef HAL_UART_Transmit(UART_HandleTypeDef *huart, uint8_t *pData, uint16_t Size, uint32_t Timeout); 参数1: UART 处理结构体的指针,该结构体包含了 UART 的所有配置参数。 参数2:要发送的数据指针 参数3&…...

Android Studio jcenter 停止服务,改用mavenCentral
随着jcenter在2021年2月28日停止服务,Android和Java开发者需寻找替代方案。推荐使用MavenCentral,可借助国内镜像加速。此外,jitpack.io也是一个选项,但对于大型项目,自建Nexus或MavenCentral更合适。迁移步骤包括更新…...

EasyPOI使用详解
EasyPOI 简介 easypoi功能如同名字easy,主打的功能就是容易,让一个没见接触过poi的人员 就可以方便的写出Excel导出,Excel模板导出,Excel导入,Word模板导出,通过简单的注解和模板 语言(熟悉的表达式语法),完成以前复杂的写法 文档:http://easypoi.mydoc.io/#categor…...

【云原生开发】K8S多集群资源管理平台架构设计
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

基于SpringBoot的城镇住房保障系统开发
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...
一文解秘Rust如何与Java互操作
本博客所有文章除特别声明外,均采用CC BY-NC-SA 4.0许可协议。转载请注明来自 唯你 使用场景 JAVA 与 Rust 互操作让 Rust 可以背靠 Java 大生态来做更多事情,而 Java 也可以享受 Rust 语言特性的内存安全,所有权机制,无畏并发。…...

手机发展史介绍
手机,这个曾经在电影和科幻小说中出现的高科技产品,如今已经渗透进了我们生活的每个角落。从单纯的通讯工具到如今集成了通讯、娱乐、工作、社交等多种功能的智能终端,手机的发展史也是人类科技进步的缩影。本文将从手机的发展历程、技术革新…...

【ArcGISPro】单次将自己建立的工具箱添加至Arcpy中
新建工具箱 添加至Arcpy中 调用刚添加的工具箱...

docker镜像仓库常用命令
docker镜像仓库常用命令 docker logindocker logoutdocker pulldocker pushdocker searchdocker imagesdocker image inspectdocker tagdocker rmidocker image prunedocker savedocker loaddocker history docker login 语法: docker login [options] [server] 功能ÿ…...

springboot 传统应用程序,适配云原生改造
概述 2024年传统应用程序上云,改造方案 1、mysql 云环境高可用方案 2、redis 云环境高可用方案 3、nginx 云环境高可用方案 4、应用 云环境高可用方案1、mysql 云环境高可用方案 1.1 你先了解 1.1.1 你先了解“mysql高可用方案” 主从复制(Master-S…...
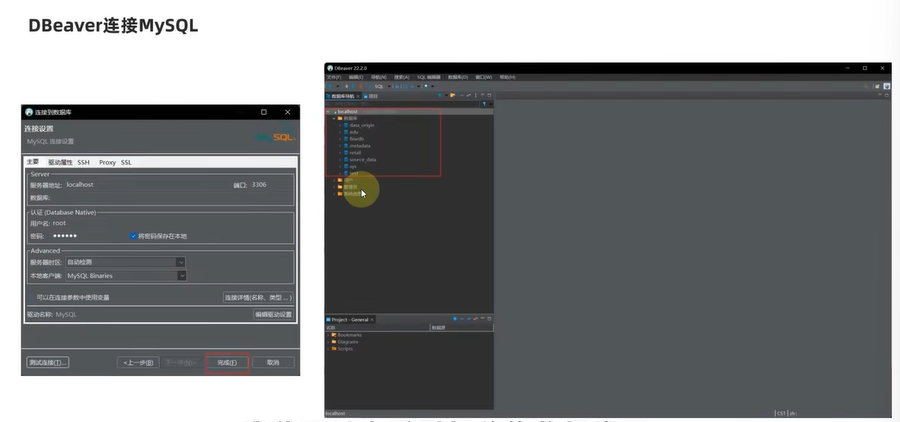
D61【python 接口自动化学习】- python基础之数据库
day61 数据库定义 学习日期:20241107 学习目标:MySQL数据库-- 130:MySQL入门使用 学习笔记: 在命令提示符内先试用MySQL 使用图形化工具操作MySQL DBeaver安装 DBeaver连接MySQL 总结 MySQL安装成功后,可以使用命…...

数据库期末考试简答题
1.试述数据、数据库、数据库管理系统、数据库系统的概念。 答:(1)数据是数据库中存储的基本对象,是描述事物的符号记录。数据有多种表现形式,它们都可以经过数字化后存入计算机。数据的种类有数字、文字、…...

Java[面试题]-真实面试
1.什么是IOC和AOP?了解么? IOC(控制反转)和AOP(面向切面编程) 1. IOC(控制反转) 概念 IOC(Inversion of Control)是面向对象编程中的一个设计原则…...

HTML5新增多媒体支持
一、引言 在当今数字化时代,丰富的多媒体内容对于网页的吸引力和用户体验至关重要。HTML5 的出现为网页带来了强大的多媒体支持,尤其是在音频和视频方面,为开发者和用户带来了全新的可能性。 二、音频audio标签 2.1 定义与属性详解 <a…...

K8S群集调度二
一、污点(Taint) 和 容忍(Tolerations) 1.1、污点(Taint) 设置在node上是对pod的一种作用 节点的亲和性,是Pod的一种属性(偏好或硬性要求),它使Pod被吸引到一类特定的节点 而Taint 则相反,它使节点能够排斥一类特…...

43.第二阶段x86游戏实战2-提取游戏里面的lua
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 本次游戏没法给 内容参考于:微尘网络安全 本人写的内容纯属胡编乱造,全都是合成造假,仅仅只是为了娱乐,请不要…...

debian系统安装qt的时候 显示xcb相关文件缺失
如果是安装之后的问题 我们可以选择使用ldd的命令查看当前依赖的so那些文件确实 ldd /home/yinsir/Qt/5.15.2/gcc_64/plugins/platforms/libqxcb.so 本人在进行打包的时候 出现则会个报错 ERROR: ldd outputLine: “libxcb-util.so.1 > not found” ERROR: for binary: “/…...

得物多模态大模型在重复商品识别上的应用和架构演进
重复商品治理介绍 根据得物的平台特性,同一个商品在平台上不能出现多个链接,原因是平台需要保证一品一链的特点,以保障商品的集中竞价,所以说一个商品在整个得物平台上只能有一个商详链接,因此我们需要对一品多链的情…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
