国内 ChatGPT中文版镜像网站整理合集（2024/11/08）
一、GPT中文镜像站
① yixiaai.com 支持GPT4、4o以及o1，支持MJ绘画
② chat.lify.vip 支持通用全模型，支持文件读取、插件、绘画、AIPPT
③ AI Chat 支持GPT3.5/4，4o以及MJ绘画
1. 什么是镜像站
镜像站（Mirror Site）是指通过复制原始网站内容和结构，创建的备用网站。其主要目的是在原始网站无法访问时，提供相同或类似的服务和信息。
2. ChatGPT 镜像站的用途
- 绕过访问限制 ：在某些地区，访问 OpenAI 官方网站可能受到限制或阻塞，镜像站可以帮助用户绕过这些限制，继续使用 ChatGPT 服务。
- 负载均衡 ：在高流量时期，镜像站可以分担部分用户请求，减轻官方服务器的负担，确保服务的稳定性。
- 备份与冗余 ：如果官方服务遇到故障或维护，镜像站可以作为备用，保证用户依然能够访问聊天机器人。
二、模型知识
1、模型基础信息
GPT-3.5 Turbo：官方已经计划下线，现在已经全面被gpt-4o-mini替代。
o1/o1-mini：最新的版本模型， o1 不是 GPT 的下一代模型！o1 和 GPT-4o在不同领域各有所长。o1 擅长 STEM领域和需要大量思考的问题，并不擅长需要常识知识的知识。OpenAI 计划在之后分别研发 GPT 和 o1 系列模型。
GPT-4o/4o-mini：性价比最高模型，支持视觉等多模态，OpenAI 文档中已经更新了 GPT-4o 的介绍：128k 上下文，训练截止 2023 年 10 月（作为对比，GPT-4-Turbo 截止 2023 年 12 月）。
GPT-4 Turbo：支持视觉等多模态，128k 上下文，训练截止 2023 年 12 月。
2、功能对比（对比热门的4o和o1）
最大区别：ChatGPT 4o支持多模态，OpenAI o1目前只支持文本内容。
能力上：OpenAI o1在推理能力上全面领先ChatGPT 4o。
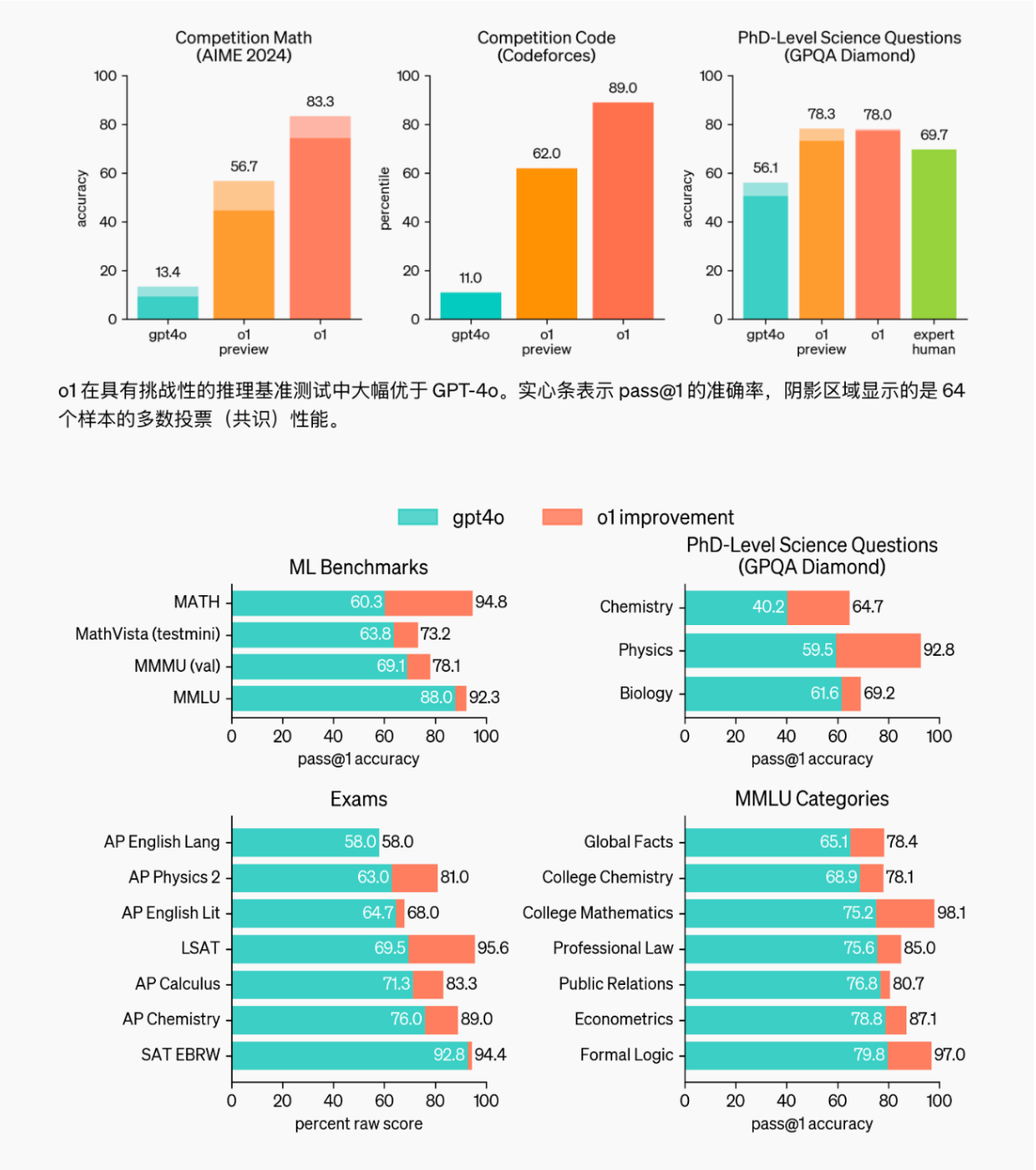
使用限制：目前ChatGPT 4o官方Plus用户没有使用限制了，o1-mini 的限额从每周 50 条增加到每天 50 条，而 o1-preview 的限额从每周 30 条提高到每周 50 条。
就我自身的使用体验来说，我更喜欢使用4o。4o整体使用更流畅，o1响应太慢。
三、国内大模型能替代？
现在好用的大模型，不仅仅ChatGPT（4.0 turbo、GPT-4o、4o mini）、Claude 模型
还有百度、智谱、阿里等的大模型。
尤其DeepSeek能力已经接近OpenAI等主流大模型。目前DeepSeek最新模型评分已经可以追上GPT-4。
而且还巨便宜，大家感兴趣的真的可以抄底~~
相关文章：
国内 ChatGPT中文版镜像网站整理合集（2024/11/08）
一、GPT中文镜像站 ① yixiaai.com 支持GPT4、4o以及o1，支持MJ绘画 ② chat.lify.vip 支持通用全模型，支持文件读取、插件、绘画、AIPPT ③ AI Chat 支持GPT3.5/4，4o以及MJ绘画 1. 什么是镜像站 镜像站（Mirror Siteÿ…...
SpringBoot整合Liquibase对数据库管理和迁移
简介 Liquibase是一个用于用于跟踪、管理和应用数据库变化的开源工具，通过日志文件(changelog)的形式记录数据库的变更(changeset)，然后执行日志文件中的修改，将数据库更新或回滚(rollback)到一致的状态。它的目标是提供一种数据库类型无关的…...
太空旅游：科技能否让星辰大海变为现实？
内容概要 在这个快速变化的时代，太空旅游成为了一个让人热血沸腾的话题。想象一下，坐在一颗漂浮的太空舱里，手中端着饮料，眺望着无尽的星辰大海，简直就像科幻电影中的情节一样。不过，这不仅仅是一个空洞的…...
[JAVAEE] 面试题(四) - 多线程下使用ArrayList涉及到的线程安全问题及解决
目录 一. 多线程下使用ArrayList 1.1. 自行判断加锁 1.2 使用Collections.synchronizedList()套壳加锁 1.3 CopyOnWriteArrayList类 二. 总结 一. 多线程下使用ArrayList 多线程下使用ArrayList会涉及到线程安全问题, 例如: public static void main(String[] args) thro…...
Elasticsearch-linux环境部署
本文主要介绍linux下elasticsearch的部署。通过在一台linux服务器中分别对elasticsearch-6.7.2版本，elasticsearch-7.3.0版本来进行安装，记录在安装elasticsearch-7.3.0版本时出现的异常情况，以及elasticsearch-head的安装。 基础环境 本机已…...
LeetCode 每日一题 长度为 K 的子数组的能量值
长度为 K 的子数组的能量值 给你一个长度为 n 的整数数组 nums 和一个正整数 k 。 一个数组的 能量值 定义为： 如果 所有 元素都是依次 连续 且 上升 的，那么能量值为 最大 的元素。 否则为 -1 。 你需要求出 nums 中所有长度为 k 的 子数组 的能量值。 …...
人工智能——小白学习指南
知孤云出岫 目录 1. **智能评测系统**2. **个性化学习路径推荐**3. **虚拟学习助手**4. **学习行为分析**5. **数据驱动的教学决策**6. **自动化课程推荐**7. **数据隐私与安全保护** 人工智能知识点的总结和学习路线，以数据表格形式呈现，并附带在教育行…...
go 集成Gin Web开发框架
引入gin的依赖 下载并安装 gin go get -u github.com/gin-gonic/gin 将 gin 引入到代码中 import "github.com/gin-gonic/gin" 开始 package mainimport "github.com/gin-gonic/gin"func main() {r : gin.Default()r.GET("/ping", func(c …...
c++ 多态性
类的多态 多态概念入门 #include <iostream> using namespace std;/* 多态的前提: 拥有继承关系的类中有相同的函数(返回类型、函数名、形参列表) 多态解决的问题：1、派生类的对象被赋值给基类对象时2、派生类的对象初始化基类的引用时3、基类的指针指向派生…...
块存储、文件存储和对象存储详细介绍
块存储、文件存储和对象存储介绍 块存储：像跑车，因为它们都能提供快速的响应和高性能，适合需要即时数据访问的场景，比如数据库和虚拟化技术。 文件存储：像货车，因为它们都能承载大量货物（文件&…...
移植 AWTK 到 纯血鸿蒙 (HarmonyOS NEXT) 系统 (9) - 编译现有的AWTK应用程序
AWTK 应用程序开发完成后，在配置文件中添加 harmonyos 的选项，通过create_project.py脚本即可生成 DevEco Studio的工程。 安装开发环境 DevEco Studio HarmonyOS 的开发工具。 Python 运行环境。 git 源码管理工具。 下载 awtk 和 awtk-harmonyos…...
ssm基于BS的仓库在线管理系统的设计与实现+vue
系统包含：源码论文 所用技术：SpringBootVueSSMMybatisMysql 免费提供给大家参考或者学习，获取源码看文章最下面 需要定制看文章最下面 目 录 第一章 绪论 1 1.1 研究背景 1 1.2 研究意义 1 1.3 研究内容 2 第二章 开发环境与技术3 …...
面试题：Spring（一）
1. Spring框架中bean是单例么？ Service Scope("singleton") public class UserServiceImpl implements UserService { }singleton : bean在每个Spring IOC容器中只有一个实例。prototype：一个bean的定义可以有多个实例。 2. Spring框架中的…...
MySQ怎么使用语法介绍（详细）
一、什么是库结构 库结构的意思就是指数据库的结构。所以，理解“库结构”就要先理解“库”是什么。 在数据库的上下文中，库指的是一个数据库。简单来说，数据库（库）是用来存储和管理数据的容器。它不仅存储实际的数据…...
新能源汽车与公共充电桩布局
近年来,全球范围内对新能源汽车产业的推动力度不断增强,中国新能源汽车市场也呈现蓬勃发展的势头,在政策与市场的共同推动下,新能源汽车销量持续增长。然而,据中国充电联盟数据显示,充电基础设施建设滞后于新能源汽车数量增长的现状导致充电桩供需不平衡,公共充电桩服务空白区域…...
【GIT】sourceTree的“当前分支“，“合并分支“与“检出分支的区别
GIT三款经典可视化 由上文文档得出灵感写出此篇 这三个概念在 Git 操作中都是很常见的， 来逐个解析： 1. 当前分支 “当前分支”就是你目前正在工作的分支。你在进行任何代码修改、提交等操作时，都会应用到“当前分支”上。换句话说…...
【Git】如何在 Git 中高效合并分支：完整指南
目录 引言1. 切换到主分支1.1 切换分支命令1.2 相关命令1.3 切换分支示意图 2. 合并分支2.1 基本合并命令2.2 合并选项2.3 合并流程示意图 3. 解决冲突3.1 解决冲突的步骤3.2 相关命令3.3 解决冲突示意图 4. 本地更新分支4.1 拉取远程更改4.2 更新主分支4.3 拉取远程更新到本地…...
成都睿明智科技有限公司抖音电商服务效果如何？
在这个短视频风起云涌的时代，抖音电商以其独特的魅力，成为了众多商家竞相追逐的新蓝海。而在这片波澜壮阔的商海中，成都睿明智科技有限公司犹如一艘稳健的航船，引领着无数企业驶向成功的彼岸。今天，就让我们一起揭开成…...
收集的linux命令/Docker命令/git命令
查看linux发行版本 lsb_release -a显示操作系统的发行版号 uname -r1. 启动 Docker。 sudo systemctl start docker2. 通过运行映像来验证 Docker 引擎安装是否成功。hello-world sudo docker run hello-world查看docker版本 docker -v查看docker配置信息 docker infodoc…...
DNS域名解析实验
准备工作 [rootlocalhost ~]# setenforce 0 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# mount /dev/sr0 /mnt [rootlocalhost ~]# dnf install bind -y DNS正向解析： 对主配置文件进行修改 [rootlocalhost ~]# vim /etc/named.conf 正向解析…...
React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook，用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途，下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库，获取股票数据，并生成TabPFN这个模型 可以识别、处理的格式，写一个完整的预处理示例，并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务，进行预测并输…...
macOS多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台（Launchpad）多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显，都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
Springcloud：Eureka 高可用集群搭建实战（服务注册与发现的底层原理与避坑指南）
引言：为什么 Eureka 依然是存量系统的核心？ 尽管 Nacos 等新注册中心崛起，但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制，是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API，查询的是单条数据，比如根据主键ID查询用户信息，sql如下： select id, name, age from user where id #{id}API默认返回的数据格式是多条的，如下： {&qu…...
)
OpenLayers 分屏对比(地图联动)
注：当前使用的是 ol 5.3.0 版本，天地图使用的key请到天地图官网申请，并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能，和卷帘图层不一样的是，分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构，使它们在 VS 解决方案资源管理器中以“组”（Filter）的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总（共4种） 方法描述是否推荐…...
企业如何增强终端安全？
在数字化转型加速的今天，企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机，到工厂里的物联网设备、智能传感器，这些终端构成了企业与外部世界连接的 “神经末梢”。然而，随着远程办公的常态化和设备接入的爆炸式…...
NXP S32K146 T-Box 携手 SD NAND（贴片式TF卡）：驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中，车辆不再仅仅是传统的交通工具，而是逐步演变为高度智能的移动终端。这一转变的核心支撑，来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒（T-Box）方案：NXP S32K146 与…...
R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...