【贪心算法】No.1---贪心算法(1)
文章目录
- 前言
- 一、贪心算法:
- 二、贪心算法示例:
- 1.1 柠檬⽔找零
- 1.2 将数组和减半的最少操作次数
- 1.3 最⼤数
- 1.4 摆动序列
- 1.5 最⻓递增⼦序列
- 1.6 递增的三元⼦序列
前言

👧个人主页:@小沈YO.
😚小编介绍:欢迎来到我的乱七八糟小星球🌝
📋专栏:贪心算法
🔑本章内容:贪心算法
记得 评论📝 +点赞👍 +收藏😽 +关注💞哦~
一、贪心算法:
贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。贪心算法解决问题的过程中,每一步都做出一个看似最优的决策,这个决策依赖于当前问题状态,不依赖于解决问题的前面的步骤和将来的步骤。这种方法在很多情况下并不会得到最优解,但是在某些问题上贪心算法的解就是最优解。
二、贪心算法示例:
1.1 柠檬⽔找零
- 题⽬链接:860. 柠檬⽔找零
- 题⽬描述

- 解法(贪⼼):
贪⼼策略:
分情况讨论:
a. 遇到 5 元钱,直接收下;
b. 遇到 10 元钱,找零 5 元钱之后,收下;
c. 遇到 20 元钱:
i. 先尝试凑 10 + 5 的组合;
ii. 如果凑不出来,拼凑 5 + 5 + 5 的组合; - C++代码
class Solution {
public:bool lemonadeChange(vector<int>& bills) {int five=0,ten=0;for(int i=0;i<bills.size();i++){if(bills[i]==5)five++;else if(bills[i]==10){ten++;if(five>0)five--;else return false;}else{if(ten>0&&five>0)//贪心{ten--;five--;}else if(five>=3)five-=3;else return false;}}return true;}
};
1.2 将数组和减半的最少操作次数
- 题⽬链接:2208. 将数组和减半的最少操作次数
- 题⽬描述:

- 解法(贪⼼):
贪⼼策略:
a. 每次挑选出「当前」数组中「最⼤」的数,然后「减半」;
b. 直到数组和减少到⾄少⼀半为⽌。
为了「快速」挑选出数组中最⼤的数,我们可以利⽤「堆」这个数据结构 - C++代码
class Solution {double sum=0,cnt=0;priority_queue<double,vector<double>,less<double>> pq;
public:int halveArray(vector<int>& nums) {for(auto&e:nums){ sum+=e;pq.push(e);}sum/=2.0;while(sum>0){cnt++;double tmp=pq.top()/2;pq.pop();sum-=tmp;pq.push(tmp);}return cnt;}
};
1.3 最⼤数
- 题⽬链接:179. 最⼤数
- 题⽬描述

- 解法(贪⼼):
可以先优化:将所有的数字当成字符串处理,那么两个数字之间的拼接操作以及⽐较操作就会很⽅便。
贪⼼策略:按照题⽬的要求,重新定义⼀个新的排序规则,然后排序即可。
排序规则:
a. 「A 拼接 B」 ⼤于 「B 拼接 A」,那么 A 在前,B 在后;
b. 「A 拼接 B」 等于 「B 拼接 A」,那么 A B 的顺序⽆所谓;
c. 「A 拼接 B」 ⼩于 「B 拼接 A」,那么 B 在前,A 在后; - C++代码
class Solution {
public:string largestNumber(vector<int>& nums) {vector<string> v;for(auto&e:nums)v.push_back(to_string(e));string ret;sort(v.begin(),v.end(),[](string& s1,string& s2){return s1+s2>s2+s1;});for(int i=0;i<v.size();i++){if(i==0&&v[i]=="0")return "0";ret+=v[i];}return ret;}
};
1.4 摆动序列
- 题⽬链接:376. 摆动序列
- 题⽬描述

- 解法(贪⼼):
贪⼼策略:
对于某⼀个位置来说:
◦ 如果接下来呈现上升趋势的话,我们让其上升到波峰的位置;
◦ 如果接下来呈现下降趋势的话,我们让其下降到波⾕的位置。
因此,如果把整个数组放在「折线图」中,我们统计出所有的波峰以及波⾕的个数即可。 - C++代码
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int left=0,ret=0;for(int i=0;i<nums.size()-1;i++){int right=nums[i+1]-nums[i];if(right==0)continue;if(right*left<=0)ret++;left=right;}return ret+1;//加上最后一个}
};
1.5 最⻓递增⼦序列
- 题⽬链接:300. 最⻓递增⼦序列
- 题⽬描述:

- 解法(贪⼼):
贪⼼策略:
我们在考虑最⻓递增⼦序列的⻓度的时候,其实并不关⼼这个序列⻓什么样⼦,我们只是关⼼最后⼀个元素是谁。这样新来⼀个元素之后,我们就可以判断是否可以拼接到它的后⾯。
因此,我们可以创建⼀个数组,统计⻓度为 x 的递增⼦序列中,最后⼀个元素是谁。为了尽可能的让这个序列更⻓,我们仅需统计⻓度为 x 的所有递增序列中最后⼀个元素的「最⼩值」。
统计的过程中发现,数组中的数呈现「递增」趋势,因此可以使⽤「⼆分」来查找插⼊位置。 - C++代码
class Solution {int cnt=0;
public:int lengthOfLIS(vector<int>& nums) {int n=nums.size();vector<int> ret;ret.push_back(nums[0]);for(int i=1;i<nums.size();i++){if(nums[i]>ret.back())ret.push_back(nums[i]);//可以拼接到后面//如果不可以拼接到末尾则需要找到ret中出现第一次>=nums[i]的值进行替换,也就是把这个第一次大的值换成小的nums[i]else{int left=0,right=ret.size()-1;while(left<right){int mid=left+(right-left)/2;if(ret[mid]>=nums[i])right=mid;else left=mid+1;}ret[left]=nums[i];}}return ret.size();}
};
1.6 递增的三元⼦序列
- 题⽬链接:334. 递增的三元⼦序列
- 题⽬描述

- 解法(贪⼼):
贪⼼策略:
最⻓递增⼦序列的简化版。
不⽤⼀个数组存数据,仅需两个变量即可。也不⽤⼆分插⼊位置,仅需两次⽐较就可以找到插⼊位置 - C++代码
class Solution {
public:bool increasingTriplet(vector<int>& nums) {int n=nums.size();vector<int> ret;ret.push_back(nums[0]);for(int i=1;i<n;i++){if(nums[i]>ret.back())ret.push_back(nums[i]);else{int left=0,right=ret.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[i]>ret[mid])left=mid+1;else right=mid;}ret[left]=nums[i];}}return ret.size()>=3?true:false;}
};
----------------------------------------------------------------------------------------------
class Solution {
public:bool increasingTriplet(vector<int>& nums) {int n=nums.size();int a=nums[0],b=INT_MAX;for(int i=1;i<n;i++){if(nums[i]>b)return true;else{if(nums[i]<=a)a=nums[i];else b=nums[i];}}return false;}
};
相关文章:

【贪心算法】No.1---贪心算法(1)
文章目录 前言一、贪心算法:二、贪心算法示例:1.1 柠檬⽔找零1.2 将数组和减半的最少操作次数1.3 最⼤数1.4 摆动序列1.5 最⻓递增⼦序列1.6 递增的三元⼦序列 前言 👧个人主页:小沈YO. 😚小编介绍:欢迎来到…...

分布式光伏管理办法
随着分布式光伏项目的不断增加,传统的管理方式已经难以满足高效、精准的管理需求。光伏业务管理系统作为一种集信息化、智能化于一体的管理工具,正在逐步成为分布式光伏项目管理的重要支撑。 光伏业务管理系统通过数字化手段实现对光伏业务全流程的精细化…...

2024最新软件测试面试热点问题
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 大厂面试热点问题 1、测试人员需要何时参加需求分析? 如果条件循序 原则上来说 是越早介入需求分析越好 因为测试人员对需求理解越深刻 对测试工…...

如何利用探商宝精准营销,抓住行业机遇——以AI技术与大数据推动企业信息精准筛选
近年来,随着人工智能与大数据技术的迅猛发展,企业的营销手段和策略发生了巨大变化。尤其是在信息爆炸的数字时代,如何有效利用这些技术在海量数据中精准找到潜在客户,已成为中小企业亟待解决的核心问题。 最近,全球人…...

嵌入式硬件电子电路设计(三)电源电路之负电源
引言:在对信号线性度放大要求非常高的应用需要使用双电源运放,比如高精度测量仪器、仪表等;那么就需要给双电源运放提供正负电源。 目录 负电源电路原理 负电源的作用 如何产生负电源 负电源能作功吗? 地的理解 负电压产生电路 BUCK电…...

数据仓库还是数据集市?这俩怎么选?
数据仓库和数据集市作为支持决策分析的两种不同方式,根据各自的特点和优势,有不同的应用场景,今天就来探讨下数据集市和数据仓库该怎么选? 一、数据集市和数据仓库对比 1、数据集市与数据仓库的关系: 1)数…...

计算机图形学 实验二 三维模型读取与控制
目录 一、实验内容 二、具体内容 (在实验2.3的基础上进行修改) 1、OFF格式三维模型文件的读取 2、三维模型的旋转动画 3、键盘鼠标的交互 4、模型的修改 三、代码 一、实验内容 读取实验提供的off格式三维模型,并对其赋色。利用鼠标和键盘的交互࿰…...

NAT网络工作原理和NAT类型
NAT基本工作流程 通常情况下,某个局域网中,只有路由器的ip是公网的,局域网中的设备都是内网ip,内网ip不具备直接与外部应用通信的能力。 处于内网的设备如何借助NAT来实现访问外网的应用? 对于开启了NAT功能的局域网…...

wget命令之Tomcat(三)
引言 Tomcat是一个开源的Java Web应用服务器,实现了多个关键的Java EE规范,包括Servlet、JSP(JavaServer Pages)、JavaWebSocket等。由于Tomcat技术先进、性能稳定且免费,它成为了许多企业和开发者的首选Web应用服务器…...
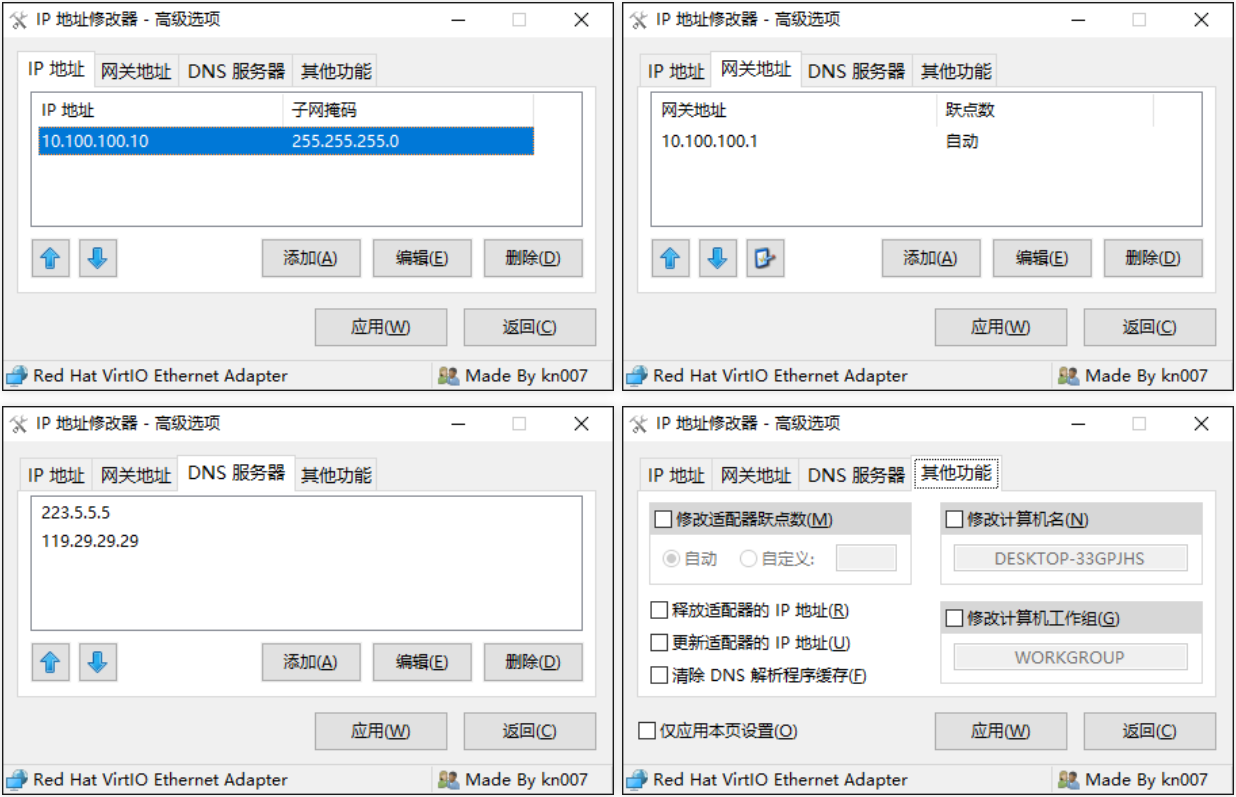
IP地址修改器 5.0 重制版
IP地址修改器是一款由 kn007 大佬编写的一个小工具,可以帮助小白用户方便的进行IP地址,网卡MAC修改等等功能,工具支持多网卡,并且支持管理导入多份配置等。 程序主要原理还是利用了WMI的Win32_NetworkAdapter、Win32_NetworkAdap…...

vscode编译s32ds工程
基本可以参考下面的文章,但是需要注意的是添加完环境变量后需要重启一下vscode。我现在已经能顺利编译。感谢原创 阿隆汽车 MBD_杂谈_使用VSCode编译s32k_vscode s32k-CSDN博客 https://blog.csdn.net/ALongAuto/article/details/134961294...

大数据专业为什么要学习Hadoop课程
在当今信息爆炸的时代,大数据成为了影响各行各业的重要因素,而Hadoop作为大数据处理的核心技术之一,自然成为大数据专业学生需要掌握的一项重要技能。本文将详细探讨大数据专业为何要学习Hadoop课程,帮助读者理解其必要性和实际应…...

Xilinx FPGA的Vivado开发流程
Xilinx FPGA 的 Vivado 开发流程主要包括以下步骤: 创建工程: 启动 Vivado 软件:双击 Vivado 图标打开软件。新建工程向导:在 Quick Start 中选择 Create Project,打开新建工程向导。设置工程信息: 工程名称…...

音频模型介绍
在处理音频数据方面,有多种模型表现出色,它们在不同的音频处理任务上有着各自的优势: 自动编码器:包括多通道变分自动编码器、自回归模型和生成对抗网络等,这些模型在音乐生成领域取得了令人印象深刻的成果。 深度生成…...

《编写沪深两市实时交易数据接收程序全攻略》
《编写沪深两市实时交易数据接收程序全攻略》 一、引言二、获取股票数据的方法(一)使用爬虫框架(二)调用股票接口(三)使用免费数据 API(四)利用 Excel 的 power query 三、数据接口及…...

一文学会easyexcel导入数据,多sheet页、字典转换【附带源码】
文章目录 前言一、业务流程二、实现1、引入easyexcel、fastjson、lombok包2、创建Json工具类3、创建自定义字典转换注解4、创建字典转换实现类5、创建数据对象类6、创建多sheet页封装对象7、创建Excel导入工具类8、创建测试类 三、接口测试1、启用项目2、使用数据导出的文件&am…...

Spring中的 InitializingBean、BeanPostProcessor、@PostConstruct 等初始化动作的执行时机分析
初始化Bean的时序图如下: 小结说明: 1、相同点:InitializingBean 的(afterPropertiesSet方法)、BeanPostProcessor、PostConstruct 都是在bean的属性注入完毕之后才执行,都可以用来进行bean的初始化动作 2、初始化执行顺序优先级…...

如何利用指纹浏览器爬虫绕过Cloudflare的防护?
网络爬虫能够系统地浏览网页并提取所需的数据,通常被用于市场研究、数据分析或者竞争情报。然而,一些反爬虫机制给网络爬虫的工作带来了不少挑战和风险。 其中,Cloudflare提供了多层次的防护机制,包括IP封锁、速率限制、CAPTCHA验…...

idea 基础简单应用(java)
Java IDE(集成开发环境)的使用方法因不同的IDE而异,但通常都包含一些基本的操作和功能。以下以IntelliJ IDEA这一流行的Java IDE为例,介绍Java IDE的基本使用方法与指南: 一、下载与安装 请点击观看 idea免费安装步…...

windows环境下vscode下载安装
vscode官网 1.vscode官网:Visual Studio Code - Code Editing. Redefined 进入官网,点击下载 右键文件,以管理员方式运行,开始安装 第一步:同意此协议 第二步:更改安装位置,可以在d盘新建一个文件夹&…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
