BFS 算法专题(四):多源 BFS
目录
1. 01 矩阵
1.1 算法原理
1.2 算法代码
2. 飞地的数量
2.1 算法原理
2.2 算法代码
3. 地图中的最高点
3.1 算法原理
3.2 算法代码
4. 地图分析
4.1 算法原理
4.2 算法代码
1. 01 矩阵
. - 力扣(LeetCode)
1.1 算法原理
- 采用 BFS + 正难则反 的解题思想, 把所有为 0 的位置为起点, 把所有为 1 的位置为终点.
- 将所有为 0 的位置加入队列中, 一层一层往外扩, 将为 1 的位置, 修改为距离 0 的最短步数
细节点: 建立一个二维数组 int[][] distance, distinct[i][j] 中存的是 [i, j] 位置距离 0 的最短路径.
dest数组的作用:
- 不需使用 boolean 数组做标记 => 将原数组中为 1 的位置, 在 dest 中初始化为 -1(特殊标记)
- 不需使用 size 记录每层中元素个数 => 借助 dest[a][b] 中的值即可(dest[x, y] = dest[a, b] + 1)
- 不需使用 step 记录扩展的层数 => 借助 dest[a][b] 中的值即可(dest[x, y] = dest[a, b] + 1)

1.2 算法代码
class Solution {public int[][] updateMatrix(int[][] mat) {int[] dx = {0, 0, 1, -1};int[] dy = {1, -1, 0, 0};int m = mat.length, n = mat[0].length;int[][] dist = new int[m][n];Queue<int[]> q = new LinkedList<>();for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {if(mat[i][j] == 0) q.offer(new int[]{i, j});else dist[i][j] = -1;}}// 以为 0 位置为起点, 一层一层往外扩while(!q.isEmpty()) {int[] t = q.poll();int a = t[0], b = t[1];for(int k = 0; k < 4; k++) {int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1) {dist[x][y] = dist[a][b] + 1;q.offer(new int[]{x, y});}}}return dist;}
}2. 飞地的数量
. - 力扣(LeetCode)
2.1 算法原理
正难则反 + 多源 BFS
- 将边界上的 1 进行入队操作
- 以边界上的 1 为起点, 进行多源 BFS, 将和其连通的其他的 1 进行标记.
- 最终, 返回内部未被标记的 1 的个数

2.2 算法代码
class Solution {public int numEnclaves(int[][] grid) {int m = grid.length, n = grid[0].length;int[] dx = {1, -1, 0, 0};int[] dy = {0, 0, 1, -1};boolean[][] check = new boolean[m][n];Queue<int[]> q = new LinkedList<>();// 将边界上的 1 入队列for(int i = 0; i < m; i++) {if(grid[i][0] == 1) q.offer(new int[]{i, 0});if(grid[i][n - 1] == 1) q.offer(new int[]{i, n - 1});}for(int j = 0; j < n; j++) {if(grid[0][j] == 1) q.offer(new int[]{0, j});if(grid[m - 1][j] == 1) q.offer(new int[]{m - 1, j});}// 多源 BFS: 将和边界上连通的 1 进行标记while(!q.isEmpty()) {int[] t = q.poll();int a = t[0], b = t[1];check[a][b] = true;for(int k = 0; k < 4; k++) {int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !check[x][y]) {check[x][y] = true;q.offer(new int[]{x, y});}}}// 统计内部不连通的 1 的个数int ret = 0;for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) if(grid[i][j] == 1 && !check[i][j]) ret++;}return ret;}
}3. 地图中的最高点
. - 力扣(LeetCode)
3.1 算法原理
- 由于任意相邻的格子高度差 至多 为 1, 所以应以水域位置为起点(水域位置固定高度为 0), 进行多源 BFS
- 将水域位置加入队列, 一层一层往外扩展.
- 每扩展到一个位置, 这个位置上的高度, 应为上个位置的高度 +1(求最高高度, 要求高度差不超过 1)

3.2 算法代码
class Solution {public int[][] highestPeak(int[][] isWater) {int m = isWater.length, n = isWater[0].length;int[][] height = new int[m][n];for(int i = 0; i < m; i++) Arrays.fill(height[i], -1);Queue<int[]> q = new LinkedList<>();for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {if(isWater[i][j] == 1) {height[i][j] = 0;q.offer(new int[]{i, j});}}}int[] dx = {1, -1, 0, 0};int[] dy = {0, 0 ,1, -1};while(!q.isEmpty()) {int[] t = q.poll();int a = t[0], b = t[1];for(int k = 0; k < 4; k++) {int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && height[x][y] == -1) {height[x][y] = height[a][b] + 1;q.offer(new int[]{x, y});}}}return height;}
}4. 地图分析
. - 力扣(LeetCode)
4.1 算法原理
-
依旧是 正难则反 + BFS
-
创建一个 dist 数值, 将陆地位置初始化为 0
-
以陆地位置为起点, 向外扩展, 扩展到的海洋位置的值是原来位置的值的基础上 +1(dist[x][y] = dist[a][b] + 1)
-
dist 数组中的最大值, 就是海洋距离陆地的最远位置
4.2 算法代码
class Solution {public int maxDistance(int[][] grid) {int m = grid.length, n = grid[0].length;int[][] dist = new int[m][n];Queue<int[]> q = new LinkedList<>();for(int i = 0; i < m; i++) Arrays.fill(dist[i], -1);// 将陆地在 dist 中的位置初始化为 0// 并入队boolean sea = false;boolean ground = false;for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {if(grid[i][j] == 1) {dist[i][j] = 0;q.offer(new int[]{i, j});}if(grid[i][j] == 0) sea = true;if(grid[i][j] == 1) ground =true;}}if(!sea || !ground) return -1;int[] dx = {1, -1, 0, 0};int[] dy = {0 ,0 , 1, -1};int ret = 0;while(!q.isEmpty()) {int[] t = q.poll();int a = t[0], b = t[1];for(int k = 0; k < 4; k++) {int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1) {dist[x][y] = dist[a][b] + 1;q.offer(new int[]{x, y});ret = Math.max(ret, dist[x][y]);}}}return ret;}
}END
相关文章:

BFS 算法专题(四):多源 BFS
目录 1. 01 矩阵 1.1 算法原理 1.2 算法代码 2. 飞地的数量 2.1 算法原理 2.2 算法代码 3. 地图中的最高点 3.1 算法原理 3.2 算法代码 4. 地图分析 4.1 算法原理 4.2 算法代码 1. 01 矩阵 . - 力扣(LeetCode) 1.1 算法原理 采用 BFS 正难…...
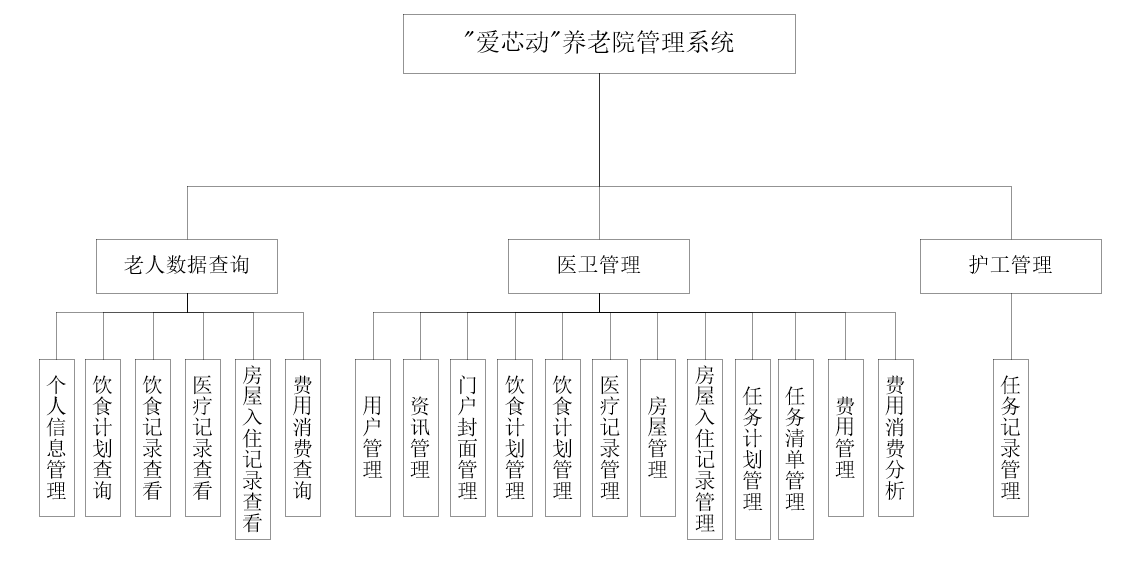
基于Spring Boot+Vue的养老院管理系统【原创】
一.系统开发工具与环境搭建 1.系统设计开发工具 后端使用Java编程语言的Spring boot框架 项目架构:B/S架构 运行环境:win10/win11、jdk17 前端: 技术:框架Vue.js;UI库:ElementUI; 开发工具&…...

Linux screen和cscope工具使用总结
1 minicom使用 1.1 minicom配置 第一次启动时: 如果输入sudo minicom提示错误,则需: sudo minicom -s 启动 出现配置菜单:选serial port setup 进入串口配置 输入A配置串口驱动为/dev/ttyUSB0 输入E配置速率为115200 8N1 输入F将 …...

深度学习面试八股汇总
按序发布: 深度学习——优化算法、激活函数、归一化、正则化 进入 深度学习——权重初始化、评估指标、梯度消失和梯度爆炸 进入 深度学习——前向传播与反向传播、神经网络(前馈神经网络与反馈神经网络)、常见算法 进入 深度学习——卷积神…...

微服务架构面试内容整理-API 网关-Gateway
Spring Cloud Gateway 是一个用于构建 API 网关的框架,它为微服务架构提供了灵活的路由和过滤功能。作为 Spring Cloud 生态的一部分,Gateway 提供了易于使用的 API 和强大的功能,适合用于现代微服务架构中的请求管理和服务交互。以下是 Spring Cloud Gateway 的主要特点、工…...

22.04Ubuntu---ROS2使用rclcpp编写节点C++
节点需要存在于功能包当中,功能包需要存在于工作空间当中。 所以我们要想创建节点,就要先创建一个工作空间,再创建功能包。 第一步:创建工作空间 mkdir -p chapt2_ws/src/ 第二步:创建example_cpp功能包,…...

XML 现实案例:深入解析与应用
XML 现实案例:深入解析与应用 XML(可扩展标记语言)自1998年成为W3C推荐标准以来,一直是数据交换和存储的重要工具。它是一种用于标记电子文件的结构化语言,使得数据不仅人类可读,而且机器可处理。本文将探讨XML在现实世界中的应用案例,展示其如何在不同领域中发挥作用。…...

Spring源码(十二):Spring MVC之Spring Boot
本篇将详细讨论Spring Boot 的启动/加载、处理请求的具体流程。我们先从一个简单的Spring Boot项目日志开始分析(这里假设读者已经仔细阅读完了前面的文章,且对Spring源码有一定深度的了解,否则会看得一脸懵逼)。 本文为2024重置…...

Kafka 之事务消息
前言: 在分布式消息系统中,事务消息也是一个热门课题,在项目的实际业务场景中,如果用到事务消息的场景也不少见,那 Kafka 作为一个高性能的分布式消息中间件,同样也支持事务消息,本篇我们将对 …...

小菜家教平台(四):基于SpringBoot+Vue打造一站式学习管理系统
前言 昨天配置完了过滤器,权限检验,基本的SpringSecurity功能已经配置的差不多了,今天继续开发,明天可能会暂停一天整理一下需求,然后就进行CRUD了。 今日进度 补充SpringSecurity异常处理和全局异常处理器 详细操作…...

解决 Vue3、Vite 和 TypeScript 开发环境下跨域的问题,实现前后端数据传递
引言 本文介绍如何在开发环境下解决 Vite 前端(端口 3000)和后端(端口 80)之间的跨域问题: 在开发环境中,前端使用的 Vite 端口与后端端口不一致,会产生跨域错误提示: Access to X…...

量化交易系统开发-实时行情自动化交易-3.3.数据采集流程
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来说说数据采集流程,后…...

探索PyAV:Python中的多媒体处理利器
文章目录 探索PyAV:Python中的多媒体处理利器第一部分:背景介绍第二部分:PyAV是什么?第三部分:如何安装PyAV?第四部分:简单的库函数使用方法1. 打开文件2. 查看流3. 遍历帧4. 编码帧5. 关闭输出…...

SpringBoot源码解析(三):启动开始阶段
SpringBoot源码系列文章 SpringBoot源码解析(一):SpringApplication构造方法 SpringBoot源码解析(二):引导上下文DefaultBootstrapContext SpringBoot源码解析(三):启动开始阶段 目录 前言一、入口二、SpringApplicationRunListener1、作用…...

C# const与readonly关键字的区别
在C#中,readonly关键字用于定义在对象创建后不能更改的字段。它可以与常量(const)有些相似,但也有显著不同。以下是readonly关键字的一些关键点: 定义与用法: readonly字段可以在类的构造函数中初始化,而const字段必须…...

【数据分享】1901-2023年我国省市县镇四级的逐年降水数据(免费获取/Shp/Excel格式)
之前我们分享过1901-2023年1km分辨率逐月降水栅格数据和Shp和Excel格式的省市县四级逐月降水数据,原始的逐月降水栅格数据来源于彭守璋学者在国家青藏高原科学数据中心平台上分享的数据!基于逐月数据我们采用求年累计值的方法得到逐年降水栅格数据&#…...
)
hhdb数据库介绍(9-4)
访问安全 权限体系 计算节点有两类用户,一类是计算节点数据库用户,用于操作数据,执行SELECT,UPDATE,DELETE,INSERT等SQL语句。另一类是关系集群数据库可视化管理平台用户,用于管理配置信息。此…...

苍穹外卖的分层所用到的技术以及工具+jwt令牌流程图(jwt验证)
分层用到的技术以及工具: jwt令牌流程图:...
Python——数列1/2,2/3,3/4,···,n/(n+1)···的一般项为Xn=n/(n+1),当n—>∞时,判断数列{Xn}是否收敛
没注释的源代码 from sympy import * n symbols(n) s n/(n1) print(数列的极限为:,limit(s,n,oo))...

css:还是语法
emmet的使用 emmet是一个插件,Emmet 是 Zen Coding 的升级版,由 Zen Coding 的原作者进行开发,可以快速的编写 HTML、CSS 以及实现其他的功能。很多文本编辑器都支持,我们只是学会使用它: 生成html结构 <!-- emme…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
