【计算机基础——数据结构——红黑树】
1. 红黑树(RBTree)
为什么HashMap不直接使用AVL树,而是选择了红黑树呢?
由于AVL树必须保证左右子树平衡,Max(最大树高-最小树高) <= 1,所以在插入的时候很容易出现不平衡的情况,一旦这样,就需要进行旋转以求达到平衡。正是由于这种严格的平衡条件,导致AVL需要花大量时间在调整上,故AVL树一般使用场景在于查询场景, 而不是 增加删除 频繁的场景。
红黑树(rbt)做了什么优化呢?
红黑树(rbt)继承了AVL可自平衡的优点,同时, 红黑树(rbt)在查询速率和平衡调整中寻找平衡,放宽了树的平衡条件,从而可以用于增加删除 频繁的场景。在实际应用中,红黑树的使用要多得多。
与AVL树相比,红黑树牺牲了部分平衡性,以换取插入/删除操作时较少的旋转操作,整体来说性能要优于AVL树。虽然RBTree是复杂的, 但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:
1.1 红黑树的特性(5条原则)
口诀:根黑叶黑,非红即黑,红黑相连,黑数相等
- 节点非黑即红
- 根节点一定是黑色
- 叶子节点(nil)一定是黑色
- 每个红色节点的两个子节点都为黑色。(等价于每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径,都包含相同数目的黑色节点。
RBT有点属于一种空间换时间类型的优化,
在avl的节点上,增加了 颜色属性的 数据,相当于 增加了空间的消耗。 通过颜色属性的增加, 换取,后面平衡操作的次数 减少。
- 红色属性 说明,红色节点的孩子,一定是黑色。 但是,RBTree 黑色节点的孩子,可以是红色,也可以是黑色。
- 叶子属性 说明, 叶子节点可以是空nil ,AVL的叶子节点不是空的,具体如下图。

基于上面的原则,我们一般在插入红黑树节点的时候,会将这个节点设置为红色,
原因参照最后一条原则: 红色破坏原则的可能性最小,如果是黑色, 很可能导致这条支路的黑色节点比其它支路的要多1,破坏了平衡。
1.2 黑色完美平衡
红黑树并不是一颗AVL平衡二叉搜索树,从图上可以看到,根节点P的左子树显然比右子树高
根据 红黑树的特性5,从任一节点到其每个叶子的所有路径,都包含相同数目的黑色节点, 说明:
rbt 的 左子树和右子树的黑节点的层数是相等的
红黑树的平衡条件,不是以整体的高度来约束的,而是以黑色节点的高度,来约束的。

去掉 rbt中的红色节点,会得到 一个四叉树, 从根节点到每一个叶子,高度相同,就是rbt的root到叶子的黑色路径长度。
1.3 红黑树的恢复平衡过程的三个操作
一旦红黑树5个原则有不满足的情况,我们视为平衡被打破,如何恢复平衡?
1.3.1 变色
节点的颜色由红变黑或由黑变红。(这个操作很好了解)
1.3.2 左旋
以某个结点作为支点(pivot),其父节点(子树的root)旋转为自己的左子树(左旋),pivot的原左子树变成 原root节点的 右子树,pivot的原右子树保持不变。

1.3.3 右旋
以某个结点作为支点(pivot),其父节点(子树的root)旋转为自己的右子树(右旋),pivot的原右子树变成 原root节点的 左子树,pivot的原左子树保持不变。

2. 红黑树插入节点情况分析
默认新插入的节点为红色,因为父节点为黑色的概率较大,插入新节点为红色,可以避免颜色冲突。
2.1 红黑树为空树
直接把插入结点作为根节点就可以了。
另外:根据红黑树性质 2根节点是黑色的。还需要把插入节点设置为黑色。
2.2 插入节点的Key已经存在
更新当前节点的值,为插入节点的值。

2.3 插入节点的父节点为黑色
由于插入的节点是红色的,当插入节点的父节点是黑色时,不会影响红黑树的平衡,所以: 直接插入无需做自平衡(因为每个节点自带两个Nil黑色节点)。

2.4 插入节点的父节点为红色
根据性质2:根节点是黑色。
如果插入节点的父节点为红色节点,那么该父节点不可能为根节点,所以插入节点总是存在祖父节点(三代关系)。
根据性质4:每个红色节点的两个子节点一定是黑色的。不能有两个红色节点相连。
此时会出现两种状态:
- 父亲和叔叔为红色
- 父亲为红色,叔叔为黑色

2.4.1 父亲和叔叔为红色节点
根据性质4:红色节点不能相连 ==》祖父节点肯定为黑色节点:
父亲为红色,那么此时该插入子树的红黑树层数的情况是:黑红红。
因为不可能同时存在两个相连的红色节点,需要进行 变色, 显然处理方式是把其改为:红黑红
变色处理:黑红红 ==> 红黑红
- 将F和V节点改为黑色
- 将P改为红色
- 将P设置为当前节点,进行后续处理

可以看到,将P设置为红色了,如果P的父节点是黑色,那么无需做处理;
但如果P的父节点是红色,则违反红黑树性质了,所以需要将P设置为当前节点,继续插入操作, 做自平衡处理,直到整体平衡为止。
2.4.2 叔叔为黑色,父亲为红色,并且父亲节点是祖父节点的左子节点

2.4.2.1 插在父亲的左节点(LL型失衡)
细分场景 1: 新插入节点,为其父节点的左子节点(LL红色情况), 插入后 就是LL 型失衡

- 变颜色:将F设置为黑色,将P设置为红色
- 对F节点进行右旋

2.4.2.2 插在父亲的右节点(LR型失衡)
细分场景 2: 新插入节点,为其父节点的右子节点(LR红色情况), 插入后 就是LR 型失衡

- 对F进行左旋
- 将F设置为当前节点,得到LL红色情况
- 按照LL红色情况处理(1.变色 2.右旋P节点)

2.4.3 叔叔为黑节点,父亲为红色,并且父亲节点是祖父节点的右子节点

2.4.3.1 RR型失衡
新插入节点,为其父节点的右子节点(RR红色情况)

自平衡处理:
1.变色:将F设置为黑色,将P设置为红色
2.对P节点进行左旋

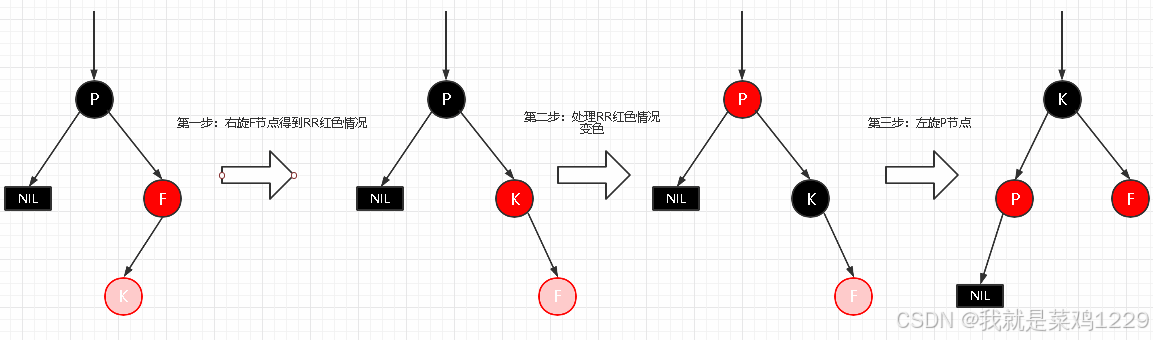
2.4.3.2 RL型失衡
新插入节点,为其父节点的左子节点(RL红色情况)

自平衡处理:
- 对F进行右旋
- 将F设置为当前节点,得到RR红色情况
- 按照RR红色情况处理(1.变色 2.左旋 P节点)
相关文章:

【计算机基础——数据结构——红黑树】
1. 红黑树(RBTree) 为什么HashMap不直接使用AVL树,而是选择了红黑树呢? 由于AVL树必须保证左右子树平衡,Max(最大树高-最小树高) < 1,所以在插入的时候很容易出现不平衡的情况,一旦这样&…...
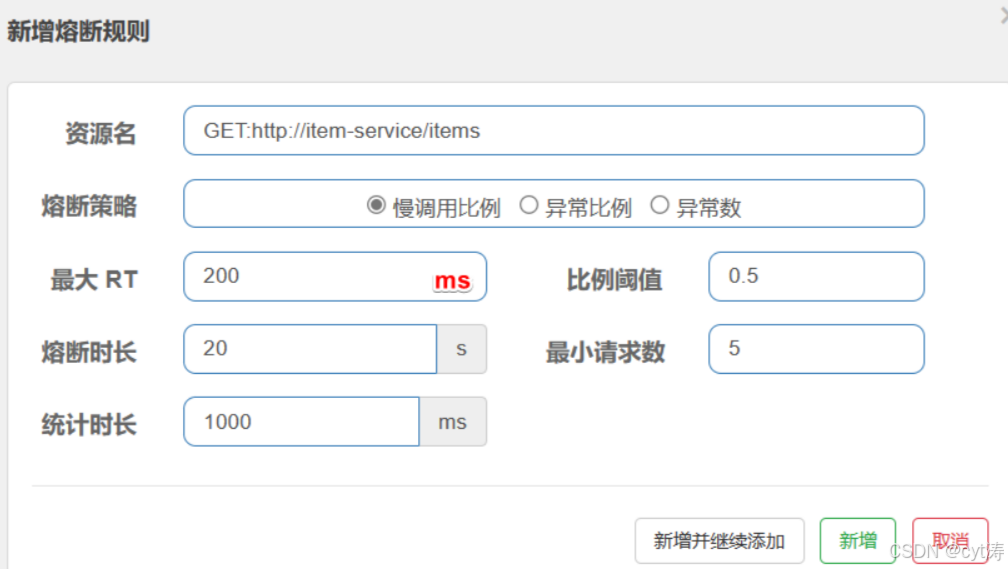
Sentinel — 微服务保护
微服务架构将大型应用程序拆分为多个小而独立的服务,每个服务可以独立部署和扩展。然而,微服务系统需要面对的挑战也随之增加,例如服务之间的依赖、分布式环境下的故障传播和安全问题。因此,微服务保护措施是确保系统在高并发、资…...

Cynet:全方位一体化安全防护工具
前言 1999年,布鲁斯施奈尔曾说过:“复杂性是安全最大的敌人。”彼时还是19年前,而现在,网络安全已然变得更加繁杂。 近日我在网上冲浪过程中发现了这么一个平台性质的软件,看似具有相当强的防护能力。 根据Cynet的描…...

python中常见的8种数据结构之一数组的应用
在Python中,数组是一种常见的数据结构,用于存储一系列相同类型的元素。在实际应用中,数组可以用于解决各种问题。 以下是数组在Python中的一些常见应用: 1. 存储和访问数据:数组可以用于存储和访问一组数据。可以通过…...

安装多个低版本谷歌Chrome浏览器用于测试,适配Vue3+vite项目
安装多个低版本谷歌Chrome浏览器用于测试,适配Vue3vite项目 问题:使用vue3tsvite搭建了一个项目,在chrome新版本浏览器上无问题,但是部署到现场页面直接空白,且控制台报错: Uncaugnt SyntaxError: Unexpe…...

UI组件---如何设置el-pagination分页组件的背景色
1. 要替换 el-pagination 组件的背景色,您可以通过自定义CSS来实现。 具体的CSS规则取决于您想要更改的是哪个部分的背景色,例如普通页码、活跃页码、上下导航箭头等。以下是一些示例CSS规则,您可以根据自己的需求进行调整: /* …...
LabVIEW编程过程中为什么会出现bug?
在LabVIEW编程过程中,Bug的产生往往源自多方面原因。以下从具体的案例角度分析一些常见的Bug成因和调试方法,以便更好地理解和预防这些问题。 1. 数据流错误 案例:在一个LabVIEW程序中,多个计算节点依赖相同的输入数据&#…...

论文阅读《Structure-from-Motion Revisited》
摘要 增量式地运动结构恢复是从无序图像集合中进行三维重建的一个普遍策略。虽然增量式地重建系统在各个方面上都取得了巨大的进步,但鲁棒性、准确性、完整度和尺度仍然是构建真正通用管道的关键问题。我们提出了一种新的运动结构恢复技术,它改进了目前…...

RK android14 第三方app获取su权限
需要修改的地方如下 frameworks/base/core/jni/com_android_internal_os_Zygote.cpp kernel-6.1/security/commoncap.c system/core/init/selinux.cpp system/core/libcutils/fs_config.cpp system/extras/su/su.cpp device/rockchip/common/BoardConfig.mk device/rockchip…...

线程与进程的区别(面试)
一.进程 进程:一个程序启动起来,就会对应一个进程,进程就是系统分配资源的基本单位。 上面一部分进程是我们自己去执行应用的可执行文件, 而另一部分是操作系统自动启动的进程. 二.线程 线程:线程是进程中的一个执行单元ÿ…...

OpenDroneMap Webodm
OpenDroneMap & Webodm OpenDroneMap Webodm 开源无人机航拍系列图像及其它系列图像三维重建软件。很棒的开源无人机测绘软件OpenDroneMap,从航拍图像生成精确的地图、高程模型、3D 模型和点云。 应用领域 Mapping & Surveying 测绘和测量 从图像测量获得高精度的可…...

Could not create task ‘:shared_preferences_android:generateDebugUnitTestConfig‘
flutter项目使用shared_preferences库的时候,打开flutter项目中的android项目运行,会出现如下错误信息: A build operation failed. Could not create task :shared_preferences_android:generateDebugUnitTestConfig. Could not create…...

CSS教程(四)- 字体
1、尺寸单位 px 像素单位% 百分比,参照父元素对应属性的值进行计算em 字体尺寸单位,参照父元素的字体大小计算,1em16pxrem字体尺寸单位,参照根元素的字体大小计算,1rem16px 2、字体属性 介绍 CSS Fonts (字体)属性用于定义字体…...

深入理解Java中的Lambda表达式
在Java 8中,Lambda表达式的引入无疑是一个重大的里程碑。 Lambda表达式以其简洁的语法和强大的功能,极大地改变了Java开发者编写代码的方式。本文将深入探讨Lambda表达式的概念、语法、使用场景以及其在函数式编程中的意义。 一、Lambda表达式的基本概…...

C#里怎么样判断一个数是偶数还是奇数
一般是采用取余的做法。 程序如下: /** C# Program to Check whether the Entered Number is Even or Odd*/ using System; using System.Collections.Generic; using System.Linq; using System.Text;namespace check1 {class Program{static void Main(string[]…...

【论文笔记】Prefix-Tuning: Optimizing Continuous Prompts for Generation
🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。 基本信息 标题: Prefix-Tuning: Optimizin…...

GNN系统学习:消息传递图神经网络
引言 在开篇中我们介绍了,为节点生成节点表征(Node Representation)是图计算任务成功的关键,我们要利用神经网络来学习节点表征。 消息传递范式是一种聚合邻接节点信息来更新中心节点信息的范式,它将卷积算子推广到了…...

基于gewe制作第一个微信聊天机器人
现在我们制作一个微信智能聊天机器人。发送文字它可以回复一段话,或一张图片,是不是有点小酷! 当然,这种智能回复的算法和数据库我们自己肯定是没有的,所以我们借助于gewe框架的开放API接口来完成我们的功能。 请求参…...

【Python】python使用Moviepy库对mp3文件进行剪切,并设置输出文件的码率
【Python】python使用Moviepy库对mp3文件进行剪切,设置输出文件的码率 一、安装Moviepy库二、代码 一、安装Moviepy库 pip install -i https://mirrors.aliyun.com/pypi/simple/ moviepy二、代码 #!/usr/bin/python # -*- coding: UTF-8 -*- from moviepy.editor …...

海外云手机在出海业务中的优势有哪些?
随着互联网技术的快速发展,海外云手机已在出海电商、海外媒体推广和游戏行业都拥有广泛的应用。对于国内的出海电商企业来说,短视频引流和社交平台推广是带来有效流量的重要手段。借助云手机,企业能够更高效地在新兴社交平台上推广产品和品牌…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
