CF862B Mahmoud and Ehab and the bipartiteness(二分图的性质)
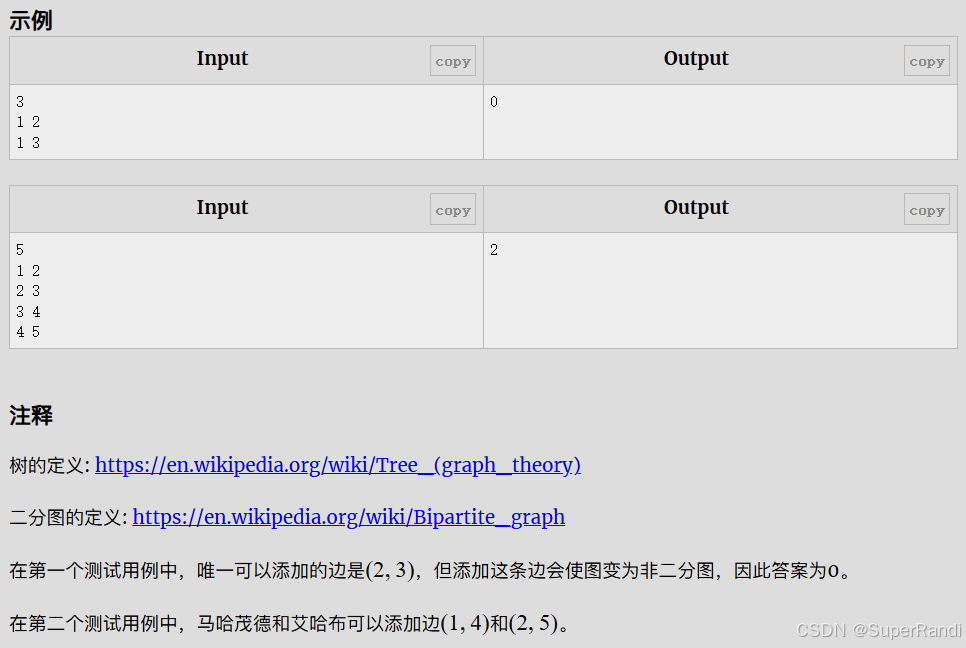
思路:一个二分图是由两个集合组成的,同一个集合中的节点间不能连边,所以一个二分图最多有cnt[1]*cnt[2]条边,题目给出一个树的n-1条边,要我们添加最多的边数使他成为二分图,添加的边数就是cnt[1]*cnt[2]-n+1条,所以我们先用dfs对每个节点进行染色,计算出两个个集合的节点数
Code:
constexpr int N=2e5+5,mod=1e9+7;int n;
int h[N],e[N],ne[N],idx;
int color[N],cnt[4];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}void dfs(int u,int c)
{color[u]=c;cnt[c]++;for(int i=h[u];~i;i=ne[i]){if(!color[e[i]]) dfs(e[i],3-c);}}void solve()
{ cin>>n;memset(h,-1,sizeof h);for(int i=1;i<=n;i++){int a,b;cin>>a>>b;add(a,b),add(b,a);} dfs(1,1);int sum=cnt[1]*cnt[2];cout<<sum-n+1;
}
相关文章:
CF862B Mahmoud and Ehab and the bipartiteness(二分图的性质)
思路:一个二分图是由两个集合组成的,同一个集合中的节点间不能连边,所以一个二分图最多有cnt[1]*cnt[2]条边,题目给出一个树的n-1条边,要我们添加最多的边数使他成为二分图,添加的边数就是cnt[1]*cnt[2]-n1…...

React Native 全栈开发实战班 :数据管理与状态之React Hooks 基础
在 React Native 应用中,数据管理与状态管理是构建复杂用户界面的关键。React 提供了多种工具和模式来处理数据流和状态管理,包括 React Hooks、Context API 以及第三方状态管理库(如 Redux)。本章节将详细介绍 React Hooks 的基础…...

传奇996_22——自动挂机
登录钩子函数中执行 callscript(actor, "../QuestDiary/主界面基础按钮/主界面基础按钮QM", "基础按钮QM")基础按钮QM执行了已下代码 #IF Equal <$CLIENTFLAG> 1 #ACT goto PC端面板加载#IF Equal <$CLIENTFLAG> 2 #ACT goto 移动端面板加载…...

faiss 提供了多种索引类型
faiss 多种索引类型 在 faiss 中,IndexFlatL2 是一个简单的基于 L2 距离(欧几里得距离)进行索引的索引类型,但实际上,faiss 提供了多种索引类型,支持不同的度量方式和性能优化,您可以根据需求选…...

比rsync更强大的文件同步工具rclone
背景 多个复制,拷贝,同步文件场景,最大规模的是每次几千万规模的小文件需要从云上对象存储中拉取到本地。其他的诸如定期数据备份,单次性数据备份。 rsync是单线程的,开源的mrsync是多线程的,但适用范围没…...

《业务流程--穿越从概念到实践的丛林》读后感一:什么是业务流程
1.1 流程和业务流程概念辨析 业务流程建模标准(BPMN)对于业务流程的定义:一个业务流程由为了配合一个组织性或技术环境而一系列活动组成。这些活动共同实现一个业务目标。 业务流程再造最有名的倡导者托马斯.H.达文波特对于流程和业务流程的定义:流程是一组结构化且可度量的…...

解决docker mysql命令行无法输入中文
docker启动时,设置支持中文 docker run --name mysql-container -e MYSQL_ROOT_PASSWORDroot -d mysql:5.7 --character-set-serverutf8mb4 --collation-serverutf8mb4_unicode_ci --default-time-zone8:00 进入docker时,指定LANG即可 docker exec -it …...
基于Java Springboot城市公交运营管理系统
一、作品包含 源码数据库设计文档万字PPT全套环境和工具资源部署教程 二、项目技术 前端技术:Html、Css、Js、Vue、Element-ui 数据库:MySQL 后端技术:Java、Spring Boot、MyBatis 三、运行环境 开发工具:IDEA/eclipse 数据…...

Lc70--319.两个数组的交集(二分查找)---Java版
1.题目描述 2.思路 用集合求交集,因为集合里面的元素要满足不重复、无序、唯一。使得集合在去重、查找和集合操作(如交集、并集、差集等)中非常高效和方便。 3.代码实现 class Solution {public int[] intersection(int[] nums1, int[] nu…...

亿咖通科技应邀出席微软汽车行业智享会,分享ECARX AutoGPT全新实践
11月14日,全球出行科技企业亿咖通科技(纳斯达克股票代码:ECX)应邀于广州参加由微软举行的汽车行业智享会,揭晓了亿咖通科技对“AI定义汽车”时代的洞察与技术布局,分享了亿咖通科技汽车垂直领域大模型ECARX…...

Python教程:运算符重载
在Python中,运算符重载是通过定义特殊方法(也称为魔术方法)来实现的,这些特殊方法允许类的实例像内置类型那样使用运算符。 Python提供了一系列这样的特殊方法,用于重载各种运算符。 以下是一些常见的运算符重载特殊…...
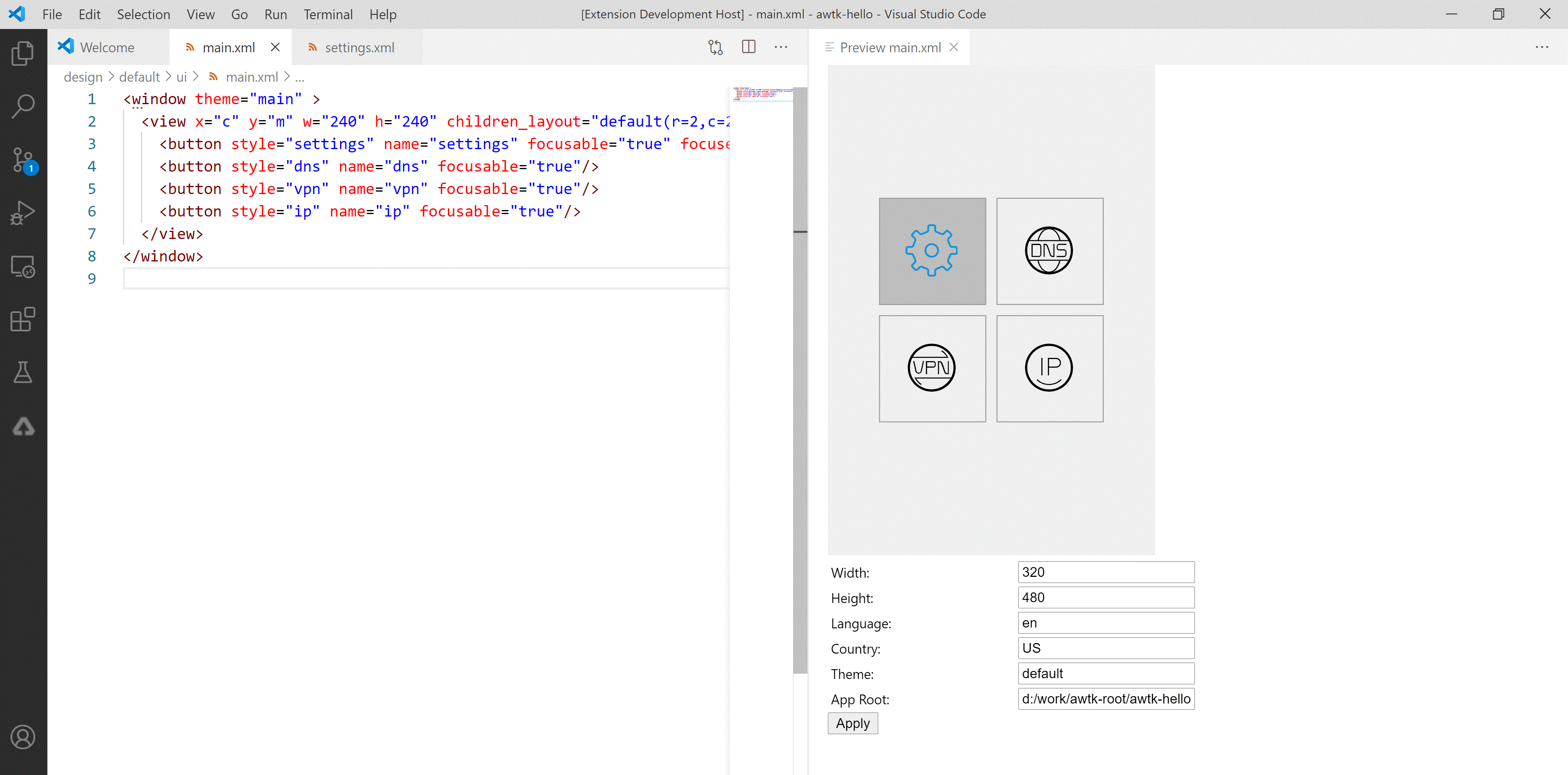
AWTK VSCode 实时预览插件端口冲突的解决办法
AWTK XML UI 预览插件:在 vscode 中实时预览 AWTK XML UI 文件,在 Copilot 的帮助下,可以大幅提高界面的开发效率。 主要特色: 真实的 UI 效果。可以设置主题,方便查看在不同主题下界面的效果。可以设置语言…...

【MySQL系列】深入理解MySQL中的存储、排序字符集
前言 在创建数据库时,我们经常会需要填写数据库的所用字符集、排序规则,字符集和排序规则是两个非常重要的概念,它们决定了数据库如何存储和比较字符串数据。在 MySQL 中,常用的存储字符集有 utf8、utf8mb4,而排序字符…...
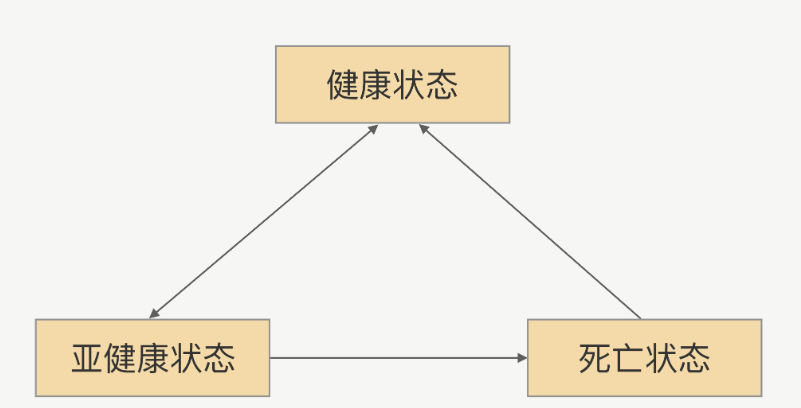
RPC-健康检测机制
什么是健康检测? 在真实环境中服务提供方是以一个集群的方式提供服务,这对于服务调用方来说,就是一个接口会有多个服务提供方同时提供服务,调用方在每次发起请求的时候都可以拿到一个可用的连接。 健康检测,能帮助从连…...
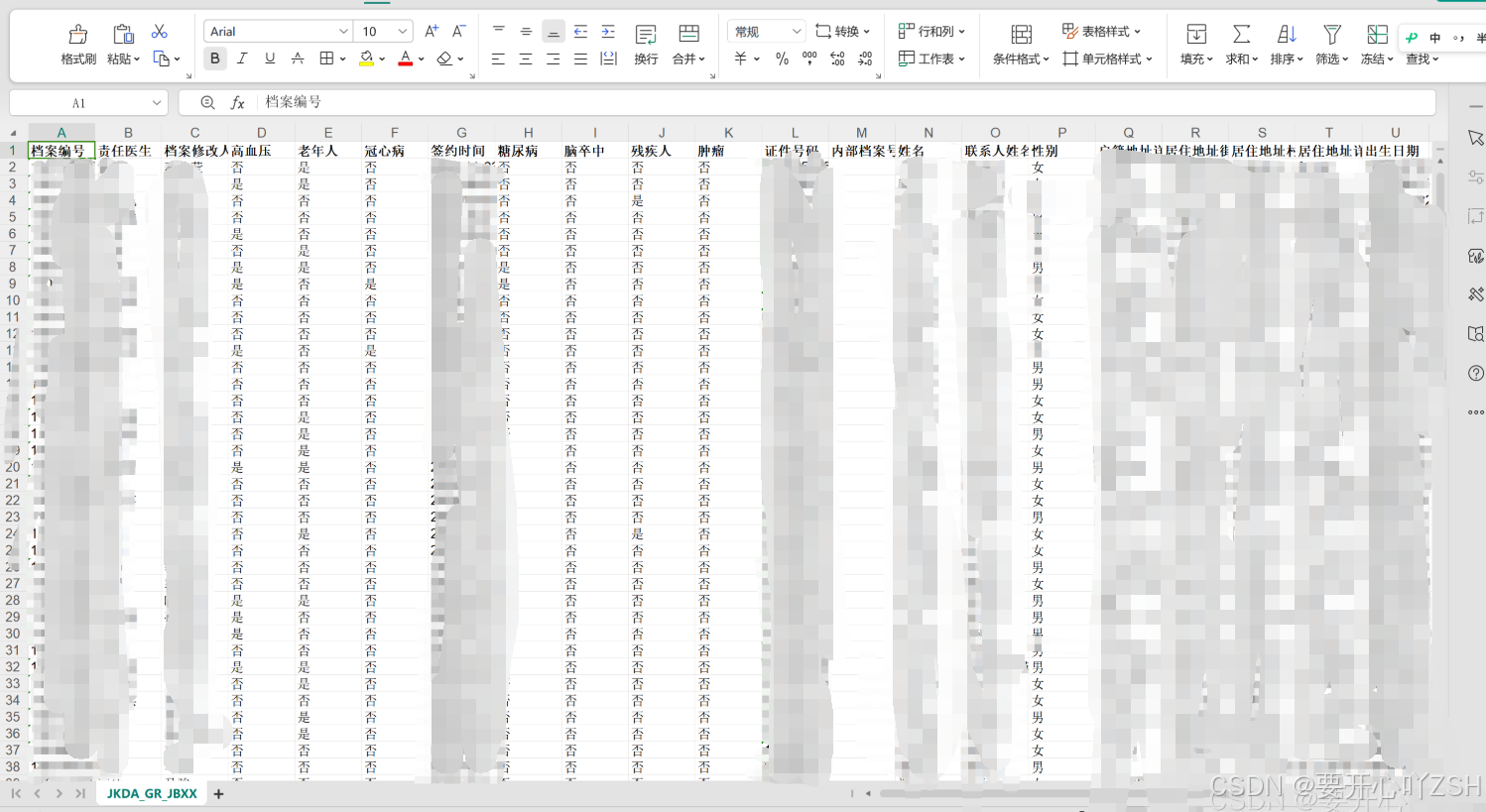
关于Java处理Excel常规列表记录,并入库的操作
1.描述 对于常规的Excel列表(二维表格)的入库处理,一般的mysql连接工具,例如Navicat就支持。但是,因为业务需要,不想每次都去手动导入,所以这里采用编码且定时任务的形式来实现。 2.Excel常规列…...

深入理解 JavaScript 中的 Array.find() 方法:原理、性能优势与实用案例详解
目录 深入理解 JavaScript 中的 Array.find() 方法:原理、性能优势与实用案例详解 一、引言:为什么要使用Array.find() 二、Array.find()的使用与技巧 1、基础语法 2、返回值 3、使用技巧 三、Array.find()的优势与实际应用案例 1、利用返回引用…...
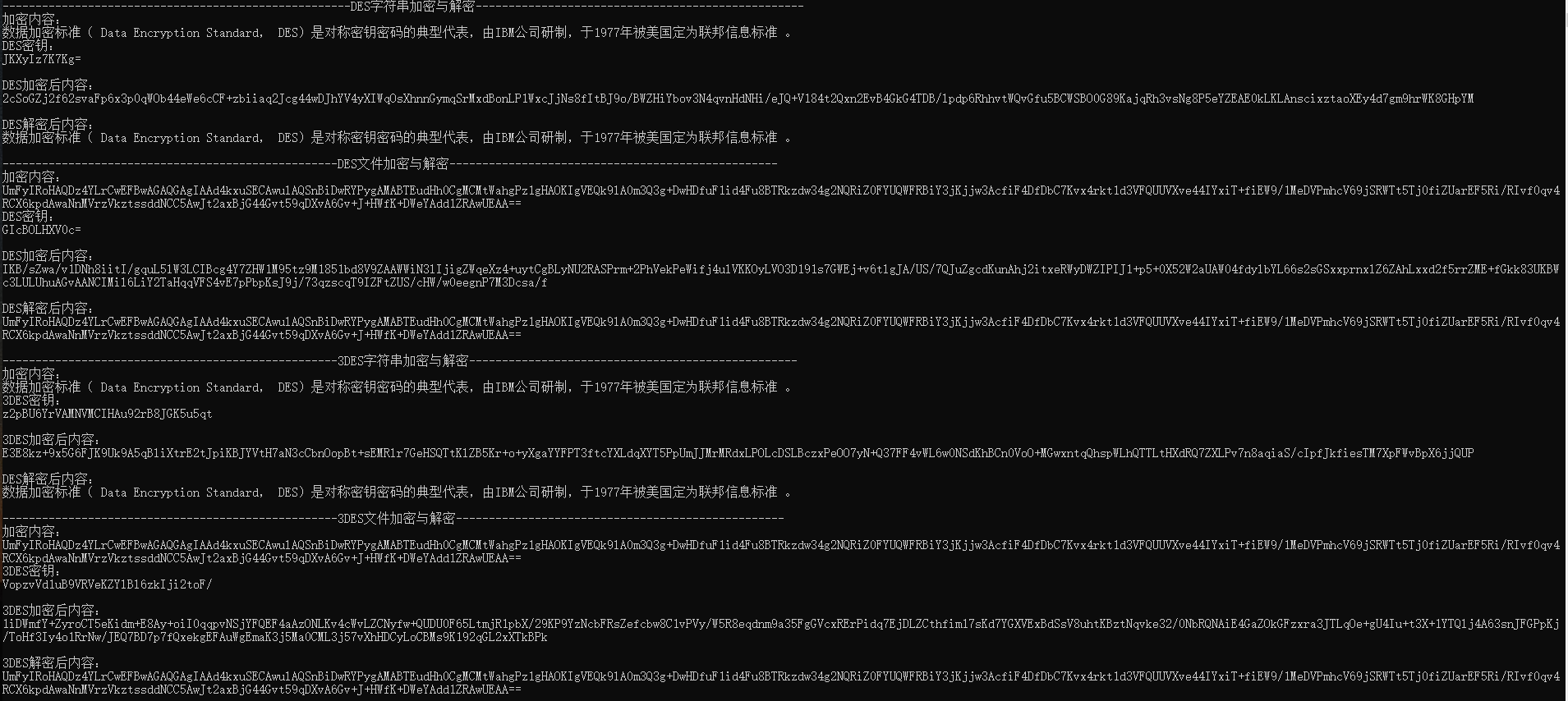
计算机网络安全 —— 对称加密算法 DES (一)
一、对称加密算法概念# 我们通过计算机网络传输数据时,如果无法防止他人窃听, 可以利用密码学技术将发送的数据变换成对任何不知道如何做逆变换的人都不可理解的形式, 从而保证了数据的机密性。这种变换被称为加密( encryptio…...
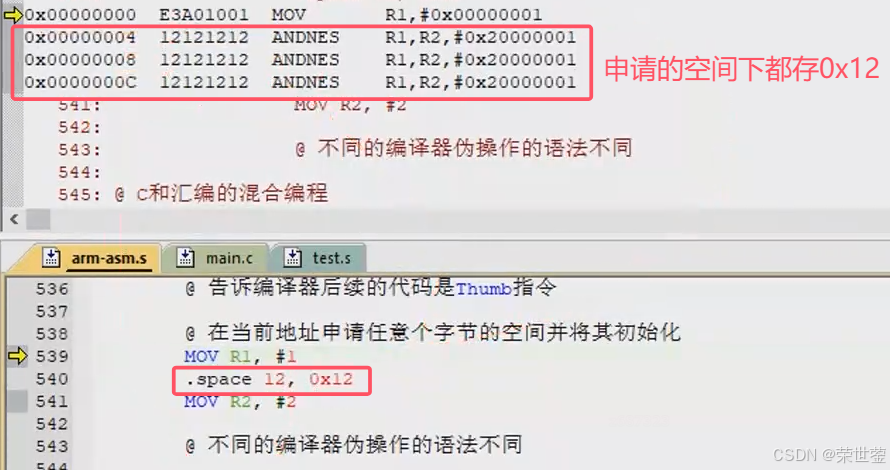
5. ARM_指令集
概述 分类 汇编中的符号: 指令:能够编译生成一条32位机器码,并且能被处理器识别和执行伪指令:本身不是指令,编译器可以将其替换成若干条指令伪操作:不会生成指令,只是在编译阶段告诉编译器怎…...

Jenkins的pipeline Script的 每个组件的详细讲解
在Jenkins的Pipeline脚本中,各个组件的配置和Groovy的一些常用函数起到了决定性的作用,帮助开发人员控制自动化流程的执行。以下是对Jenkins Pipeline的主要组件和Groovy常用函数的详细讲解: 1. Jenkins Pipeline主要组件 1.1 agent 功能&…...

Tomcat 和 Netty 的区别及应用场景分析
在 Java Web 开发中,Tomcat 和 Netty 都是常见的网络框架,它们各自有着不同的设计理念和适用场景。本文将通过详细的对比和实际场景示例,帮助你理解 Tomcat 和 Netty 在功能、性能、架构等方面的差异,帮助你在实际开发中做出更合理…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

