STL-stack栈:P1981 [NOIP2013 普及组] 表达式求值
这个题用的STL-栈来做
题目来源:洛谷
相关知识

[NOIP2013 普及组] 表达式求值
题目背景
NOIP2013 普及组 T2
题目描述
给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。
输入格式
一行,为需要你计算的表达式,表达式中只包含数字、加法运算符 + 和乘法运算符 *,且没有括号,所有参与运算的数字均为 0 0 0 到 2 31 − 1 2^{31}-1 231−1 之间的整数。
输入数据保证这一行只有 0123456789+* 这 12 12 12 种字符。
输出格式
一个整数,表示这个表达式的值。
注意:当答案长度多于 4 4 4 位时,请只输出最后 $ 4$ 位,前导 $ 0$ 不输出。
样例 #1
样例输入 #1
1+1*3+4
样例输出 #1
8
样例 #2
样例输入 #2
1+1234567890*1
样例输出 #2
7891
样例 #3
样例输入 #3
1+1000000003*1
样例输出 #3
4
提示
对于 30 % 30\% 30% 的数据, 0 ≤ 0≤ 0≤ 表达式中加法运算符和乘法运算符的总数 ≤ 100 ≤100 ≤100。
对于 80 % 80\% 80% 的数据, 0 ≤ 0≤ 0≤ 表达式中加法运算符和乘法运算符的总数 ≤ 1000 ≤1000 ≤1000。
对于 100 % 100\% 100% 的数据, 0 ≤ 0≤ 0≤ 表达式中加法运算符和乘法运算符的总数 ≤ 100000 ≤100000 ≤100000。
题意
求出一个只含*和+的表达式的值(中缀表达式),但是值只输出后四位(去除前导0)
思路
-
题目因为只有*和+就相对简单。表达式求值可以用栈来做,字符串储存数据然后分别压入栈处理。但因为某个数字是字符串如:12345 ,所以需要特殊处理,遇到下一个符号/换行符时,才会得到该数据
if (isdigit(c)) {num = num * 10 + (c - '0'); isdigit(c) 计算机C(C++)语言中的一个函数,主要用于检查其参数是否为十进制数字字符。} -
只有两个运算符,因为考虑优先级,所以符号就没必要压入栈,只需要即将运算的数据放入栈中,每次遇到符号后就处理:计算当前表达式
a +/* b,将结果压入栈即可。但什么时候压栈?什么时候出栈? -
可以考虑栈中只存放所有相加的数据,即:将优先级高的 *先计算出来!
如: k+a*b+c
- a*b的结果要当遍历到b时,才会计算结果,而要确定b这个数据(像12345 这个数字,就是字符串遍历到5之后如果出现了字符’+'才会确定),就需要遇到下一个符号时才会计算,即:考虑用变量储存b之前的符号,当遍历完b后,把计算a*b的相乘的结果,并储存当前运算符。

- a*b的结果要当遍历到b时,才会计算结果,而要确定b这个数据(像12345 这个数字,就是字符串遍历到5之后如果出现了字符’+'才会确定),就需要遇到下一个符号时才会计算,即:考虑用变量储存b之前的符号,当遍历完b后,把计算a*b的相乘的结果,并储存当前运算符。
-
题目要求只输出最后四位,我们只需要将每一个压入栈的数据%10000即可!注意是四个0!。而前导0 的问题,由于计算都是用int类型,%10000后会自动去掉无效的前导0
数据约束
暂无
参考代码
#include <bits/stdc++.h>
using namespace std;
int m = 10000;
int main() {string a;getline(cin, a); // 读取表达式stack<int> s; // 栈用于存储数值int num = 0; // 临时存储当前数字char op = '+'; // 当前操作符,初始化为加号for (int i = 0; i < a.size(); i++) {char c = a[i];// 如果是数字 isdigit(c) 计算机C(C++)语言中的一个函数,主要用于检查其参数是否为十进制数字字符。if (isdigit(c)) {num = num * 10 + (c - '0');}// 如果是运算符或者是最后一个字符if (!isdigit(c)|| i == a.size() - 1) {if (op == '+') {s.push(num%m); // 当前是加法,直接入栈} else if (op == '*') {int top = s.top();s.pop();s.push((top * num)%m); // 当前是乘法,和栈顶数值进行乘法运算} op = c; // 更新操作符num = 0; // 重置当前数字}}// 计算结果int result = 0;while (!s.empty()) {result += s.top();result %= m;s.pop();}cout << result; // 输出计算结果return 0;
}相关文章:

STL-stack栈:P1981 [NOIP2013 普及组] 表达式求值
这个题用的STL-栈来做 题目来源:洛谷 相关知识 [NOIP2013 普及组] 表达式求值 题目背景 NOIP2013 普及组 T2 题目描述 给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。 输入格式 一行,为需要你计算的表达式ÿ…...

Java使用stream进行分组汇总失效问题
背景 在当前项目的开发任务中需要定制财务报表导出功能,格式比较特殊使用了VM。在汇总数据的过程中使用了stream.collect 进行分组汇总。在测试的过程中发现分组失败,最终原因是对象的对比方式问题,collect是根据对象对比的所以需要重写equa…...

VMWare虚拟机安装华为欧拉系统
记录一下安装步骤: 1.在vmware中创建一个新的虚拟机,步骤和创建centos差不多 2.启动系统 具体的看下图: 启动虚拟机 耐心等待 等待进度条走完重启系统就完成了...

阿里云轻量应用服务器可以用在哪些场景呢
在数字化转型的浪潮中,中小企业面临着如何快速、高效地上云的挑战。阿里云轻量应用服务器(SWAS)作为一款专为中小企业设计的云服务产品,提供了简单易用、经济实惠的解决方案,助力企业轻松实现云端部署,赋能…...

OrangePi 5plus yolov5 部署全过程
准备工作 一、下载用户手册 下载-Orange Pi官网-香橙派(Orange Pi)开发板,开源硬件,开源软件,开源芯片,电脑键盘 里面有详细的镜像烧录教程和桌面使用等 二、镜像下载 准备一张TF卡(32G以上),插入电脑,…...

Rust中::和.的区别
在 Rust 中,:: 和 . 是两种常用的操作符,它们的作用和语法用途不同。以下是详细的对比和解释: 1. ::(双冒号) :: 是 路径操作符,主要用于访问模块、结构体、枚举、函数、常量等的命名空间中的成员。 主要…...

集群聊天服务器(7)数据模块
目录 Mysql数据库代码封装头文件与源文件 Mysql数据库代码封装 业务层代码不要直接写数据库,因为业务层和数据层的代码逻辑也想完全区分开。万一不想存储mysql,想存redis的话,就要改动大量业务代码。解耦合就是改起来很方便。 首先需要安装m…...

VS Code 更改背景颜色
我们的 VS code 默认是 黑色,这个颜色在有光的情况下,个人感觉反光比较严重。 所以换成白色了。 步骤: 选择 File -> Preferences -> Settings Workbench -> Appearance -> Color Theme -> 选择喜欢的颜色 选择后会变为你选…...

OpenAI 助力数据分析中的模式识别与趋势预测
数据分析师的日常工作中,发现数据中的隐藏模式和预测未来趋势是非常重要的一环。借助 OpenAI 的强大语言模型(如 GPT-4),我们可以轻松完成这些任务,无需深厚的编程基础,也能快速上手。 在本文中࿰…...
IDM扩展添加到Edge浏览器
IDM扩展添加到Edge浏览器 一般情况下,当安装IDM软件后,该软件将会自动将IDM Integration Module浏览器扩展安装到Edge浏览器上,但在某些情况下,需要我们手动安装,以下为手动安装步骤 手动安装IDM扩展到Edge浏览器 打…...
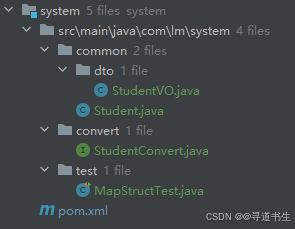
【SpringBoot】26 实体映射工具(MapStruct)
Gitee 仓库 https://gitee.com/Lin_DH/system 介绍 现状 为了让应用程序的代码更易于维护,通常会将项目进行分层。在《阿里巴巴 Java 开发手册》中,推荐分层如下图所示: 每层都有对应的领域模型,即不同类型的 Bean。 DO&…...

分层架构 IM 系统之架构演进
在电商业务日活几百万的情况下,IM 系统采用分层架构方式,如下图。 分层架构的 IM 系统,整体上包含了【终端层】、【入口层】、【业务逻辑层】、【路由层】、【数据访问层】和【存储层】,我们在上篇文章(分层架构 IM 系…...
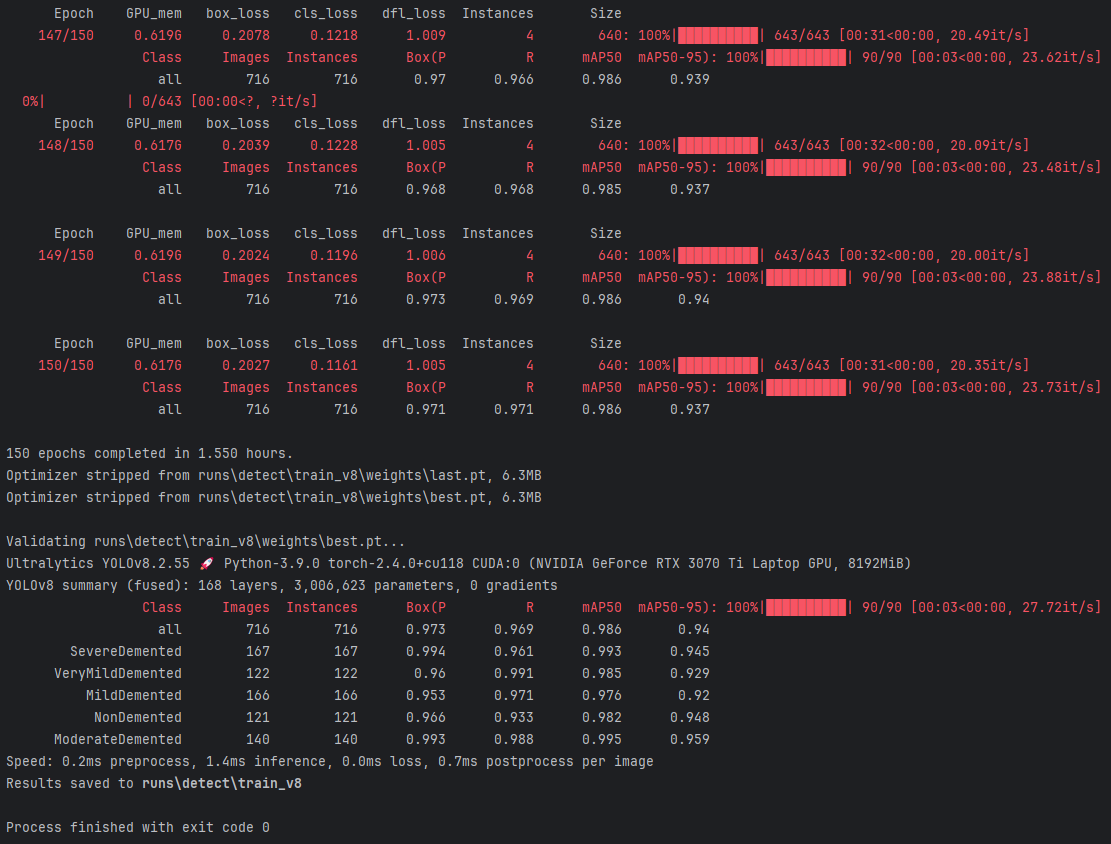
基于YOLOv8深度学习的医学影像阿尔兹海默症检测诊断系统研究与实现(PyQt5界面+数据集+训练代码)
阿尔茨海默症(Alzheimer’s disease)是一种常见的神经退行性疾病,主要表现为记忆丧失、认知能力下降以及行为和人格改变。随着全球老龄化问题的加剧,阿尔茨海默症的发病率也在逐年上升,给患者及其家庭带来了巨大的经济…...

【支持向量机(SVM)】:相关概念及API使用
文章目录 1 SVM相关概念1.1 SVM引入1.1.1 SVM思想1.1.2 SVM分类1.1.3 线性可分、线性和非线性的区分 1.2 SVM概念1.3 支持向量概念1.4 软间隔和硬间隔1.5 惩罚系数C1.6 核函数 2 SVM API使用2.1 LinearSVC API 说明2.2 鸢尾花数据集案例2.3 惩罚参数C的影响 1 SVM相关概念 1.1…...

Android kotlin之配置kapt编译器插件
配置项目目录下的gradle/libs.versions.toml文件,添加kapt配置项: 在模块目录下build.gradle.kt中增加 plugins {alias(libs.plugins.android.application)alias(libs.plugins.jetbrains.kotlin.android)// 增加该行alias(libs.plugins.jetbrains.kotl…...

时序数据库TDEngine
TDengine 是一款开源、高性能、云原生的时序数据库(Time Series Database, TSDB), 它专为物联网、车联网、工业互联网、金融、IT 运维等场景优化设计。同时它还带有内建的缓存、流式计算、数据订阅等系统功能,能大幅减少系统设计的复杂度&…...

jd-easyflow中inclusive的用法
在jd-easyflow中,inclusive通常与流程中的条件分支(conditions)配置相关,用于控制多个条件分支的执行逻辑。当conditionType设置为inclusive时,表示多个条件分支中的所有条件都会被评估,而不是像exclusive那…...

sqlmap图形化安装使用(附文件)
1.需要python环境,我这里就不教如何安装python环境了。 2.下载压缩包并且解压 3. 凭自己喜好选择大窗口小窗口 4.进入图形化界面后,1.输入url地址。2.选择要执行的操作。3.构造命令语句 5.点击一把梭,然后就可以发现出结果了 6. 对于喜欢自己…...

从二维到一维:动态规划矩阵问题的优化之道
动态规划中的矩阵问题是非常经典的应用场景,比如最小路径和问题。这类问题很自然地可以想到使用二维 dp 数组来求解。 我们定义: dp[i][j] 表示从矩阵的第 i行第 j列到右下角的最小路径和。 基本解法 求解过程从右下角开始,向左上角遍历&am…...
:让机器看懂世界)
计算机视觉(CV):让机器看懂世界
引言 计算机视觉(Computer Vision, CV)是人工智能的重要领域,致力于让机器能够“看懂”世界。CV技术广泛应用于自动驾驶、医疗影像、安防监控和娱乐领域,正在改变我们的生活方式。 本文将从基本概念、技术方法、应用场景和发展方向…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
