关联度分析、灰色预测GM(1,1)、GM(1,1)残差模型——基于Python实现
关联度分析
import numpy as np
import pandas as pd
#关联度分析
#参考序列
Y_0=[170,174,197,216.4,235.8]
#被比较序列
Y_1=[195.4,189.9,187.2,205,222.7]
Y_2=[308,310,295,346,367]#初始化序列
X_0=np.array(Y_0)/Y_0[0]
X_1=np.array(Y_1)/Y_1[0]
X_2=np.array(Y_2)/Y_2[0]#计算绝对差序列
deta1=np.abs(X_0-X_1)
deta2=np.abs(X_0-X_2)#计算deta1,deta2最小值
min1=np.min([np.min(deta1),np.min(deta2)])
max1=np.max([np.max(deta1),np.max(deta2)])#计算关联系数yita
rio=0.5
yita1 = [(min1 + rio * max1) / (deta1[i] + rio * max1) for i in range(len(deta1))]#计算关联系数yita1
yita2 = [(min1 + rio * max1) / (deta2[i] + rio * max1) for i in range(len(deta2))]#计算关联系数yita2
# #计算关联度
r1=np.mean(yita1)
r2=np.mean(yita2)
# 创建DataFrame
df = pd.DataFrame({'yita1': yita1,'yita2': yita2
})
#更改索引
df.index = ['1','2','3','4','5']print('关联度分析:')
print(df)
#输出关联度
print('关联度:',r1,r2)关联度分析:yita1 yita2
1 1.000000 1.000000
2 0.705293 0.878928
3 0.381163 0.380878
4 0.355909 0.452620
5 0.333333 0.387478
关联度: 0.5551396262321364 0.6199809489771715
灰色预测GM(1,1)模型
from math import exp
#原始序列
X_0=(6,20,40,25,45,35,21,14,18,15.5,17,15)
#累加生成序列
X_1 = np.cumsum(X_0)
#print('累加生成序列:', X_1)
#构造矩阵B和数据向量Y
B = np.zeros((len(X_1)-1,2))
Y = X_0[1:]
for i in range(len(X_1)-1):B[i][0] = -0.5*(X_1[i]+X_1[i+1])B[i][1] = 1#print('矩阵B:', B)
#print('数据向量Y:', Y)
#计算参数a,b
A = np.dot(np.dot(np.linalg.inv(np.dot(B.T,B)),B.T),Y)
a = A[0]
miu = A[1]
#计算预测模型
X_1_predict = np.zeros(len(X_0))
X_1_predict[0] = X_0[0]
for i in range(1, len(X_0)):X_1_predict[i] = ((X_0[0] - miu / a) * exp(-a * i) + miu / a)
#预测方程式
print('预测方程式:', 'X_1_(k+1) = ', X_0[0]- miu/ a, '*exp(-', a, '*i) +', miu/ a)
预测方程式: X_1_(k+1) = -476.05668934240276 *exp(- 0.0746651965600655 *i) + 482.05668934240276
模型检验
#残差检验
X_1_predict = np.zeros(len(X_0))
X_1_predict[0] = X_0[0]
for i in range(1,len(X_0)):X_1_predict[i] = ((X_0[0]-miu/a)*exp(-a*i)+miu/a)print('预测值:', X_1_predict)
#累减生成序列X_0_predict
X_0_predict = np.zeros(len(X_0))
X_0_predict[0] = X_0[0]
for i in range(1,len(X_0)):X_0_predict[i] = X_1_predict[i] - X_1_predict[i-1]#累减生成序列
print('累减生成序列:', X_0_predict)
预测值: [ 6. 40.25030314 72.03643912 101.53569452 128.91260092154.31985252 177.8991578 199.78202993 220.09052023 238.93789892256.42928694 272.66224218]
累减生成序列: [ 6. 34.25030314 31.78613597 29.4992554 27.3769064 25.407251623.57930529 21.88287213 20.30849029 18.8473787 17.49138802 16.23295524]
# X_0_predict
#计算绝对误差
error = np.abs(X_0_predict-X_0)
print('绝对误差:', error)
绝对误差: [ 0. 14.25030314 8.21386403 4.4992554 17.6230936 9.59274842.57930529 7.88287213 2.30849029 3.3473787 0.49138802 1.23295524]
#计算相对误差
error_rate = error/X_0
#输出相对误差,保留四位小数,输出百分比
print('相对误差:', np.round(error_rate,4)*100,'%')相对误差: [ 0. 71.25 20.53 18. 39.16 27.41 12.28 56.31 12.82 21.6 2.89 8.22] %
#输出检验表,包括原始序列,预测序列,残差序列,绝对误差,相对误差
df = pd.DataFrame({'原始序列': X_0,'预测序列': X_1_predict,'残差序列': X_0_predict,'绝对误差': error,'相对误差': error_rate
})
df.index = ['1','2','3','4','5','6','7','8','9','10','11','12']
print('检验表:')
print(df)
检验表:原始序列 预测序列 残差序列 绝对误差 相对误差
1 6.0 6.000000 6.000000 0.000000 0.000000
2 20.0 40.250303 34.250303 14.250303 0.712515
3 40.0 72.036439 31.786136 8.213864 0.205347
4 25.0 101.535695 29.499255 4.499255 0.179970
5 45.0 128.912601 27.376906 17.623094 0.391624
6 35.0 154.319853 25.407252 9.592748 0.274079
7 21.0 177.899158 23.579305 2.579305 0.122824
8 14.0 199.782030 21.882872 7.882872 0.563062
9 18.0 220.090520 20.308490 2.308490 0.128249
10 15.5 238.937899 18.847379 3.347379 0.215960
11 17.0 256.429287 17.491388 0.491388 0.028905
12 15.0 272.662242 16.232955 1.232955 0.082197
相对误差大于于0.5%,模型检验不通过
GM(1,1)残差模型
#残差模型进行修正
#对erroe序列进行GM(1,1)模型预测
#原始序列
X_0 = error
#累加生成序列
X_1 = np.cumsum(X_0)
#构造矩阵B和数据向量Y
B = np.zeros((len(X_1)-1,2))
Y = X_0[1:]
for i in range(len(X_1)-1):B[i][0] = -0.5*(X_1[i]+X_1[i+1])B[i][1] = 1
#计算参数a,b
A = np.dot(np.dot(np.linalg.inv(np.dot(B.T,B)),B.T),Y)
a = A[0]
miu = A[1]
#计算预测模型
X_1_predict = np.zeros(len(X_0))
X_1_predict[0] = X_0[0]
for i in range(1, len(X_0)):X_1_predict[i] = ((X_0[0] - miu / a) * exp(-a * i) + miu / a)
# #预测方程式
print('预测方程式:', 'X_1_(k+1) = ', X_0[0]- miu/ a, '*exp(-', a, '*k) +', miu/ a)
预测方程式: X_1_(k+1) = -47.4894117559714 *exp(- 0.21716818506240565 *k) + 47.4894117559714
#修正后的模型为原始模型加上求导后的方程式
# Differentiate the prediction equation with respect to k
X_1_predict_derivative = np.zeros(len(X_0))for i in range(1, len(X_0)):deta3= 1 if (i + 1) >= 2 else 0X_1_predict_derivative[i] = -a * (X_0[0] - miu / a) * exp(-a * (i-1)) * deta3# Corrected model by adding the differentiated equation to the original model
X_1_corrected = X_1_predict + X_1_predict_derivativeprint('修正后的模型:', X_1_corrected)
#输出修正后的模型方程式
print('修正后的模型方程式:', 'X_1_(k+1) = ', X_0[0]- miu/ a, '*exp(-', a, '*k) +', miu/ a, ' - ', -a*(X_0[0] - miu/a), 'deta(k-1)*exp(-',a, '*k) ')
#输出修正后的模型方程式,分开为k>=2,k<2
print('修正后的模型方程式:', 'X_1_(k+1) = ', X_0[0]- miu/ a, '*exp(-', a, '*k) +', miu/ a, ' - ', -a*(X_0[0] - miu/a), 'deta(k-1)*exp(-',a, '*(k-1)) ', 'k>=2')
print('修正后的模型方程式:', 'X_1_(k+1) = ', X_0[0]- miu/ a, '*exp(-', a, '*k) +', miu/ a, 'k<2')
修正后的模型: [ 0. 19.58337881 25.03078704 29.41483178 32.94308733 35.7826083638.06783956 39.90698129 41.38711264 42.57831436 43.53698707 44.3085217 ]
修正后的模型方程式: X_1_(k+1) = -47.4894117559714 *exp(- 0.21716818506240565 *k) + 47.4894117559714 - 10.31318936072558 deta(k-1)*exp(- 0.21716818506240565 *k)
修正后的模型方程式: X_1_(k+1) = -47.4894117559714 *exp(- 0.21716818506240565 *k) + 47.4894117559714 - 10.31318936072558 deta(k-1)*exp(- 0.21716818506240565 *(k-1)) k>=2
修正后的模型方程式: X_1_(k+1) = -47.4894117559714 *exp(- 0.21716818506240565 *k) + 47.4894117559714 k<2
#残差检验
X_1_corrected
#累减生成序列
X_0_corrected = np.zeros(len(X_1_corrected))
X_0_corrected[0] = X_1_corrected[0]
for i in range(1, len(X_1_corrected)):X_0_corrected[i] = X_1_corrected[i] - X_1_corrected[i-1]print('累减生成序列:', X_0_corrected)
累减生成序列: [ 0. 19.58337881 5.44740823 4.38404474 3.52825555 2.839521032.2852312 1.83914174 1.48013134 1.19120172 0.95867271 0.77153463]
# X_0_predict
#计算绝对误差
error = np.abs(X_0_corrected-X_0)
print('绝对误差:', error)
绝对误差: [0. 6.11131907 4.55574461 1.15568474 7.53661955 1.187444440.14100682 2.03499833 0.386519 0.73109566 1.00028958 0.07505627]
#计算相对误差
X_0=(6,20,40,25,45,35,21,14,18,15.5,17,15)
error_rate = error/X_0
#输出相对误差,保留四位小数,输出百分比
print('相对误差:', np.round(error_rate,4)*100,'%')
相对误差: [ 0. 30.56 11.39 4.62 16.75 3.39 0.67 14.54 2.15 4.72 5.88 0.5 ] %
#输出检验表,包括原始序列,预测序列,残差序列,绝对误差,相对误差
df = pd.DataFrame({'原始序列': X_0,'预测序列': X_1_corrected,'残差序列': X_0_corrected,'绝对误差': error,'相对误差': error_rate
})
df.index = ['1','2','3','4','5','6','7','8','9','10','11','12']
print('检验表:')
print(df)检验表:原始序列 预测序列 残差序列 绝对误差 相对误差
1 6.0 0.000000 0.000000 0.000000 0.000000
2 20.0 19.583379 19.583379 6.111319 0.305566
3 40.0 25.030787 5.447408 4.555745 0.113894
4 25.0 29.414832 4.384045 1.155685 0.046227
5 45.0 32.943087 3.528256 7.536620 0.167480
6 35.0 35.782608 2.839521 1.187444 0.033927
7 21.0 38.067840 2.285231 0.141007 0.006715
8 14.0 39.906981 1.839142 2.034998 0.145357
9 18.0 41.387113 1.480131 0.386519 0.021473
10 15.5 42.578314 1.191202 0.731096 0.047167
11 17.0 43.536987 0.958673 1.000290 0.058841
12 15.0 44.308522 0.771535 0.075056 0.005004
修正后的模型检验通过,模型预测准确
预测
#预测13月份的数据
X_13_predict = ((X_0[0]-miu/a)*exp(-a*12)+miu/a)
print('13月份的预测值:', X_13_predict)
13月份的预测值: 76.46124387795606
相关文章:
、GM(1,1)残差模型——基于Python实现)
关联度分析、灰色预测GM(1,1)、GM(1,1)残差模型——基于Python实现
关联度分析 import numpy as np import pandas as pd #关联度分析 #参考序列 Y_0[170,174,197,216.4,235.8] #被比较序列 Y_1[195.4,189.9,187.2,205,222.7] Y_2[308,310,295,346,367]#初始化序列 X_0np.array(Y_0)/Y_0[0] X_1np.array(Y_1)/Y_1[0] X_2np.array(Y_2)/Y_2[0]#计…...
)
linux常用命令(网络相关)
目录 1. ping - 检查网络连通性 参数 示例 2. ifconfig - 配置网络接口 参数 示例 3. ip - 显示和操作路由、网络设备、接口等 参数 示例 4. netstat - 显示网络连接、路由表、接口统计等信息 参数 示例 5. ss - 更快的netstat替代品 参数 示例 6. nslookup - …...

【uni-app多端】修复stmopjs下plus-websocket无心跳的问题
从这篇文章接着向下看: uniapp plus-websocket 和stompjs连接教程 安卓ios手机端有效 - 简书 按照文章的方式,能够实现APP下stmopjs长连接。但是有一个问题,就是会频繁输出 res-创建连接-1- 跟踪连接,会发现连接都会在大约40s后…...

VScode学习前端-01
小问题合集: vscode按!有时候没反应,有时候出来,是因为------>必须在英文状态下输入! 把鼠标放在函数、变量等上面,会自动弹出提示,但挡住视线,有点不习惯。 打开file->pre…...

Java-05 深入浅出 MyBatis - 配置深入 动态 SQL 参数、循环、片段
点一下关注吧!!!非常感谢!!持续更新!!! 大数据篇正在更新!https://blog.csdn.net/w776341482/category_12713819.html 目前已经更新到了: MyBatisÿ…...

突破自动驾驶瓶颈!KoMA:多智能体与大模型的完美融合
0.简介 本推文主要介绍了由来自北京航空航天大学的姜克谋、蔡轩和崔智勇教授等共同提出的一种名为KoMA的知识驱动的多智能体框架。论文《KoMA: Knowledge-driven Multi-agent Framework for Autonomous Driving with Large Language Models》提出了KoMA框架,通过结…...

YOLO入门教程(三)——训练自己YOLO11实例分割模型并预测【含教程源码+一键分类数据集 + 故障排查】
目录 引言前期准备Step0 环境部署1.安装OpenCV2.安装Pytorch3.安装Ultralytics Step1 打标训练Step2 格式转换Step3 整理训练集Step4 训练数据集4.1创建yaml文件4.2训练4.3预测4.4故障排查4.4.1OpenCV版本故障,把OpenCV版本升级到4.0以上4.4.2NumPy版本故障…...

【加入默语老师的私域】C#面试题
什么是依赖注入,如何实现? 依赖注入是一种设计模式。我们不是直接在另一个类(依赖类)中创建一个类的对象,而是将对象作为参数传递给依赖类的构造函数。它有助于编写松散耦合的代码,并有助于使代码更加模块…...
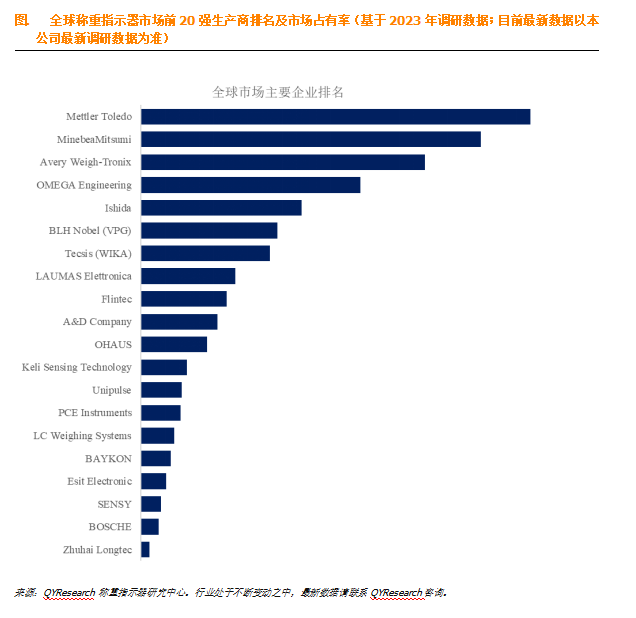
称重传感器指示器行业全面且深入的分析
称重传感器指示器是一种用于显示和解释称重传感器输出信号的设备,用于测量力、重量或压力。称重传感器是将物理力(如重量)转换为电信号的传感器,称重传感器指示器将该电信号转换为可读格式,通常以磅、公斤或牛顿等单位…...

NAT网络地址转换——Easy IP
NAT网络地址转换 Tip: EasylP没有地址池的概念,使用接口地址作为NAT转换的公有地址。EasylP适用于不具备固定公网IP地址的场景:如通过DHCP, PPPOE拨号获取地址的私有网络出口,可以直接使用获取到的动态地址进行转换。 本次实验模拟nat协议配置 AR1配置如下&…...
【Visual Studio系列教程】如何在 VS 上编程?
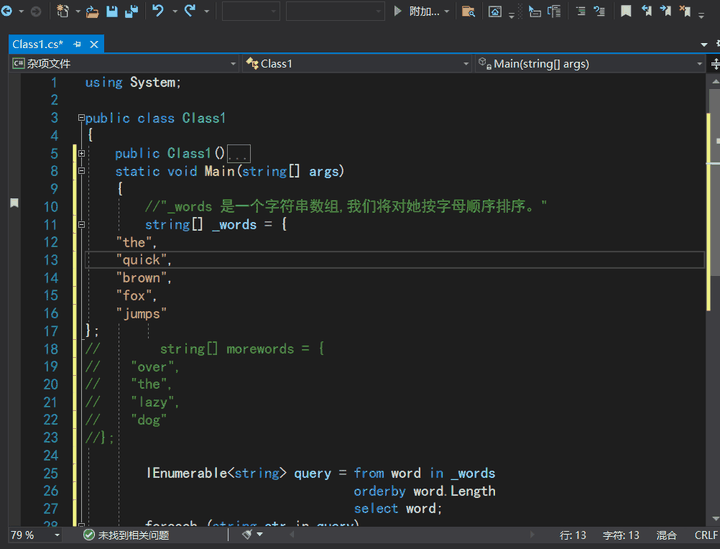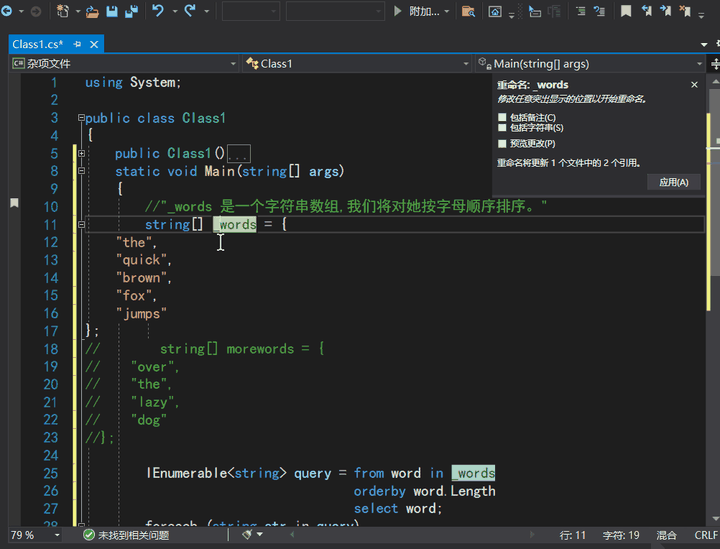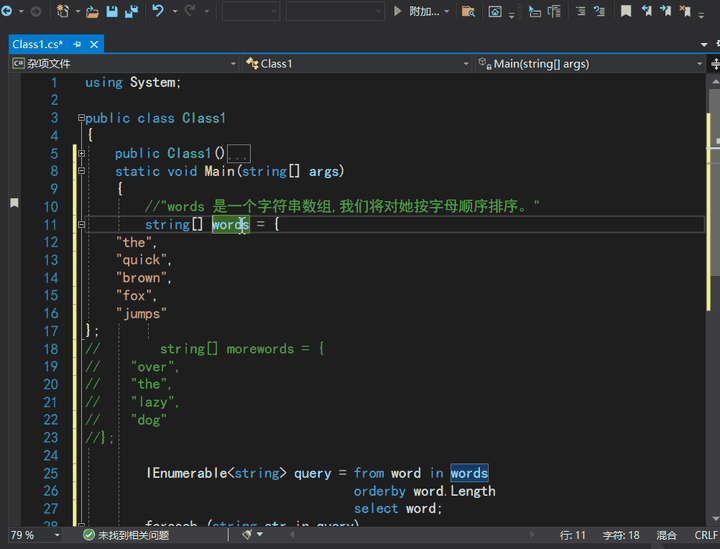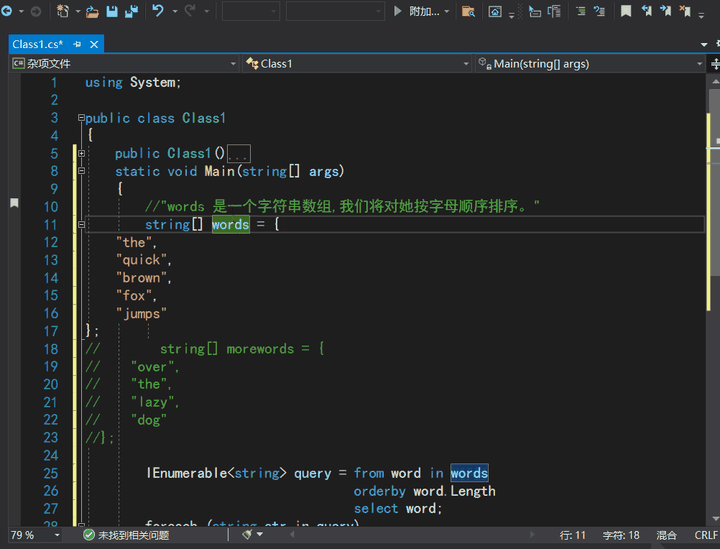
上一篇博客中,我们介绍了《什么是 Visual Studio?》。本文,我们来看第2篇《如何在 VS 上编程?》。阅读本文大约10 分钟。我们会向文件中添加代码,了解 Visual Studio 编写、导航和了解代码的简便方法。 本文假定&…...

Mybatis-Plus 多租户插件属性自动赋值
文章目录 1、Mybatis-Plus 多租户插件1.1、属性介绍1.2、使用多租户插件mavenymlThreadLocalUtil实现 定义,注入租户处理器插件测试domianservice & ServiceImplmapper 测试mapper.xml 方式 1.3、不使用多租户插件 2、实体对象的属性自动赋值使用1. 定义实体类2. 实现 Meta…...

AWTK-WIDGET-WEB-VIEW 实现笔记 (4) - Ubuntu
Ubuntu 上实现 AWTK-WIDGET-WEB-VIEW 开始以为很简单,后来发现是最麻烦的。因为 Ubuntu 上的 webview 库是 基于 GTK 的,而 AWTK 是基于 X11 的,两者的窗口系统不同,所以期间踩了几个大坑。 1. 编译 AWTK 在使用 Linux 的输入法时…...
--高级函数特性详解)
Python入门(7)--高级函数特性详解
Python高级函数特性详解 🚀 目录 匿名函数(Lambda)装饰器的使用生成器与迭代器递归函数应用实战案例:文件批处理工具 1. 匿名函数(Lambda)深入解析 🎯 1.1 Lambda函数基础与进阶 1.1.1 基本…...

【数据库原理】理解数据库,基础知识
第一代:网状数据库;第二代:关系数据库;第三代:新一代数据库系统BigData 一、理解数据库 什么是数据:信息,对事物的存在方方式、运动状态及特征的描述。数据,记录信息的识别方式有数…...

VConsole——(H5调试工具)前端开发使用于手机端查看控制台和请求发送
因为开发钉钉H5微应用在手机上一直查看不到日志等,出现安卓和苹果上传图片一边是成功的,一边是失败的,所以找了这个,之前在开发微信小程序进行调试的时候能看到,之前没想到过,这次被人提点发现可以单独使用…...

论文分享 | FuzzLLM:一种用于发现大语言模型中越狱漏洞的通用模糊测试框架
大语言模型是当前人工智能领域的前沿研究方向,在安全性方面大语言模型存在一些挑战和问题。分享一篇发表于2024年ICASSP会议的论文FuzzLLM,它设计了一种模糊测试框架,利用模型的能力去测试模型对越狱攻击的防护水平。 论文摘要 大语言模型中…...

vmWare虚拟环境centos7安装Hadoop 伪分布式实践
背景:近期在研发大数据中台,需要研究Hadoop hive 的各种特性,需要搭建一个Hadoop的虚拟环境,本来想着使用dock ,但突然发现docker 公共仓库的镜像 被XX 了,无奈重新使用vm 搭建虚拟机。 大概经历了6个小时完…...
】半小时入门C++开发(深入理解new+List+范围for+可变参数))
【C++入门(一)】半小时入门C++开发(深入理解new+List+范围for+可变参数)
目录 一.深入理解new 使用格式 二.List列表 定义一个列表 迭代器 添加元素 删除元素 排序 反转序列 三.范围for 四.可变参数 std::initializer_list 可变参数模板(variadic template) 一.深入理解new 类似于C语言中的malloc、calloc和reallo…...

Vue 3与TypeScript集成指南:构建类型安全的前端应用
在Vue 3中使用TypeScript,可以让你的组件更加健壮和易于维护。以下是使用TypeScript与Vue 3结合的详细步骤和知识点: 1. 环境搭建 首先,确保你安装了Node.js(推荐使用最新的LTS版本)和npm或Yarn。然后,安…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
